1주차. DES와 AES + CryptoHack

한샛코드·2025년 3월 18일
암호
0

@Xpert

목록 보기
1/4
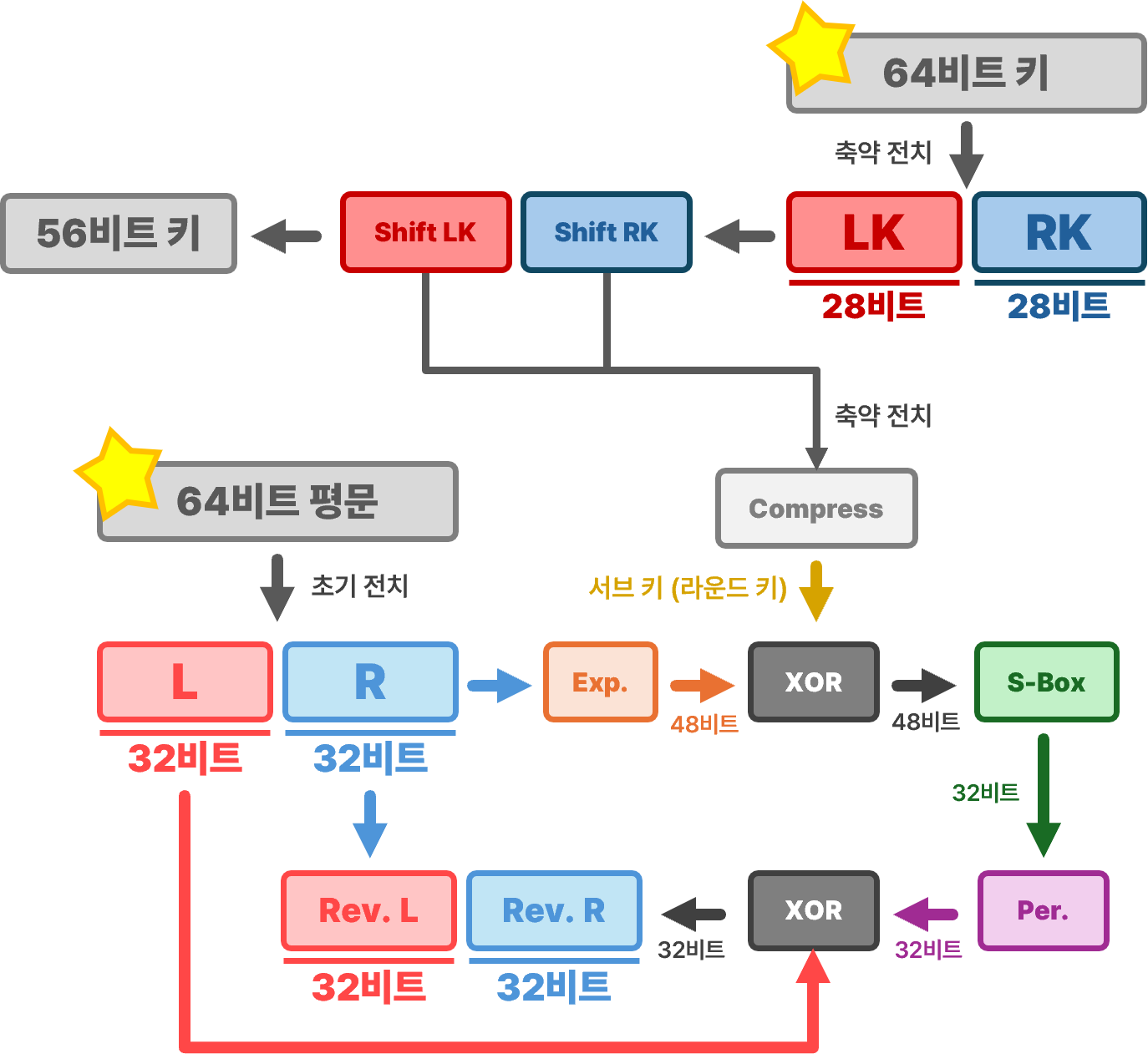
post-thumbnail

DES(Data Encryption Standard; 데이터 암호화 표준)

대칭 키 암호화 중 블록 암호의 일종으로, 페이스텔(Feistel) 암호 구조를 사용함

  1. 대칭 키 암호(symmetric-key algorithm) - 암·복호화에 모두 같은 키를 사용하는 암호 알고리즘
    • 암호화 및 복호화 속도가 빠른 장점이 있지만, 대칭키 공유 과정에서 해킹 위험에 노출됨
  2. 블록 암호(block cipher) - 평문을 블록 단위로 나누어 암·복호화하는 것
    • DES는 64비트 크기의 블록 단위로 암·복호화를 진행함

핵심 알고리즘

0. 초기 전치 (IP; Initial Permutation)

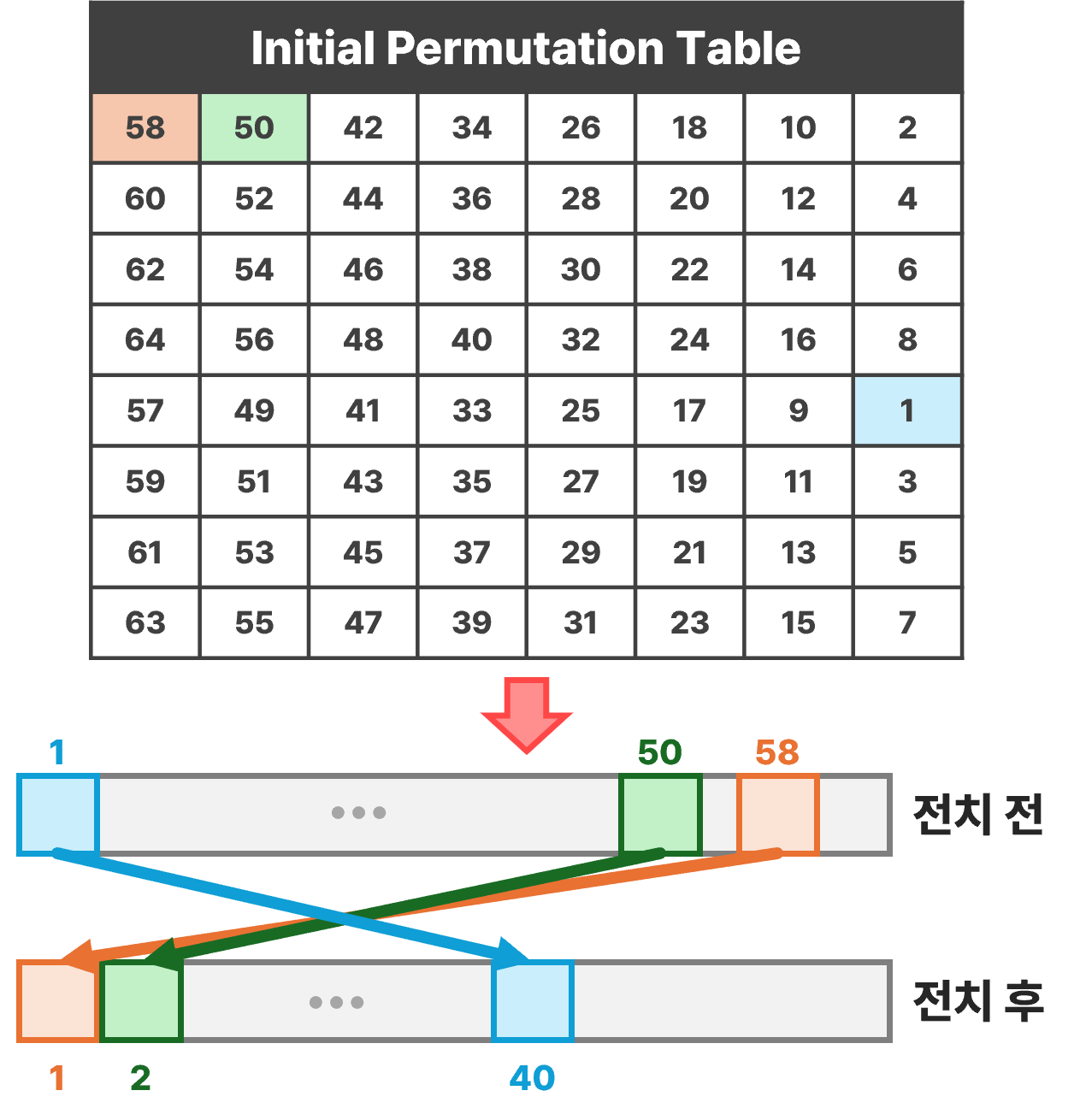
  • 64비트의 평문 블록을 초기 전치표(IP Table)에 기재된 규칙대로 섞음
    • 58번째 비트 값을 1번째로, 50번째 비트 값을 2번째로 ... 등
    • 모든 비트값의 순서를 바꿈
  • 초기 전치가 끝난 후, 전치한 블록을 절반으로 나누어 왼쪽과 오른쪽으로 나눔
    • 즉, 왼쪽 블록과 오른쪽 블록은 모두 32비트로 나누어짐

1. 확장 전치 (Expansion Permutation)

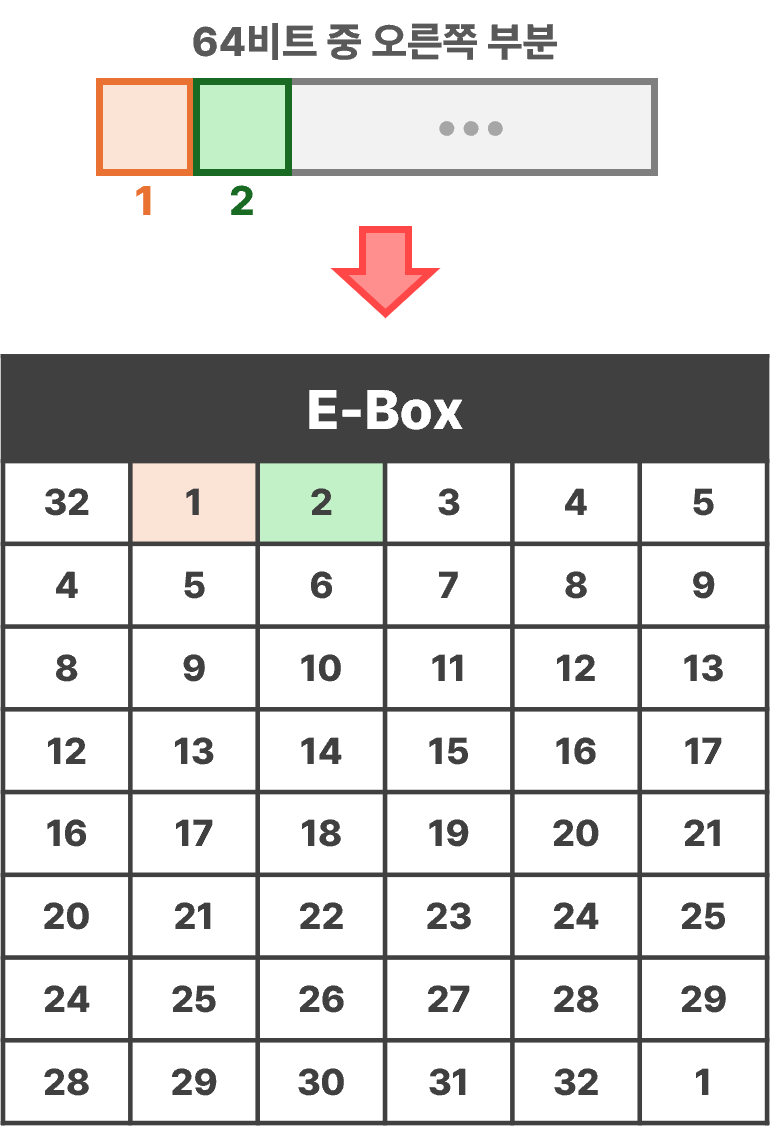
  • 오른쪽 블록(32비트)을 확장 전치표(E-Box)에 기재된 규칙대로 섞음
    • 16개의 일부 비트를 중복시켜 48비트로 확장함
      • 1, 4, 5, 8, 9, 12, 13, 16, 17, 20, 21, 24, 25, 28, 29, 32번째 비트
    • 32번째 비트를 1번째로, 1번째 비트를 2번째로 ... 등
  • 다음 순서에 48비트의 라운드 키와의 XOR(Exclusive OR)연산을 하기 위함

2. XOR(Exclusive-OR) 연산 with 라운드 키

XOR을 사용하는 중요한 이유는 가역성(암호화→복호화)을 유지하기 위함

  • 비선형성(입력과 출력관계가 비례하지 않음)을 통해 암호의 강도를 높임
  • 복호화 할 때, 자기 자신과의 XOR 연산이 원래 값을 되돌려 줌
    • A XOR B XOR B = A XOR 0 = A
    • 즉, 복호화 과정에서 동일한 라운드 키를 같은 순서로 사용하여 복호화 가능

3. S-Box (Substitution Boxes) 연산

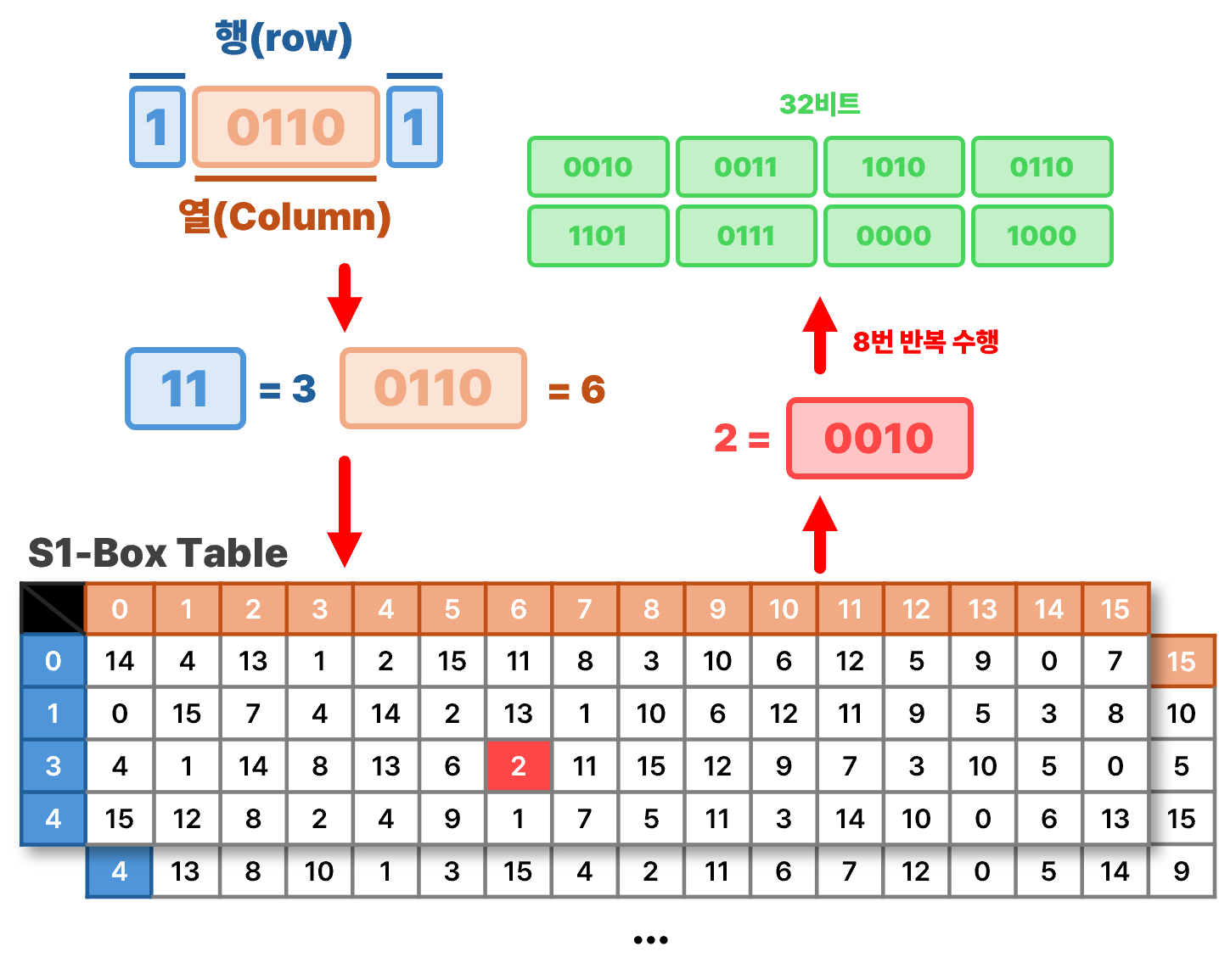
  • XOR 연산을 거치고 나온 48비트를 6비트씩 나누어서 S-Box 연산을 수행함
    • S-Box 연산 → 6비트의 양 끝의 2비트는 행(row), 그 사이 4비트는 열(column)을 나타냄
    • 매 6비트마다 똑같은 S-Box를 쓰는 것이 아니라, 각각 다른 S-Box를 사용함
  • 해당 연산은 48비트 ÷ 6비트 = 8번을 수행하여, 8번 × 4비트 = 32비트를 결과값으로 내놓음

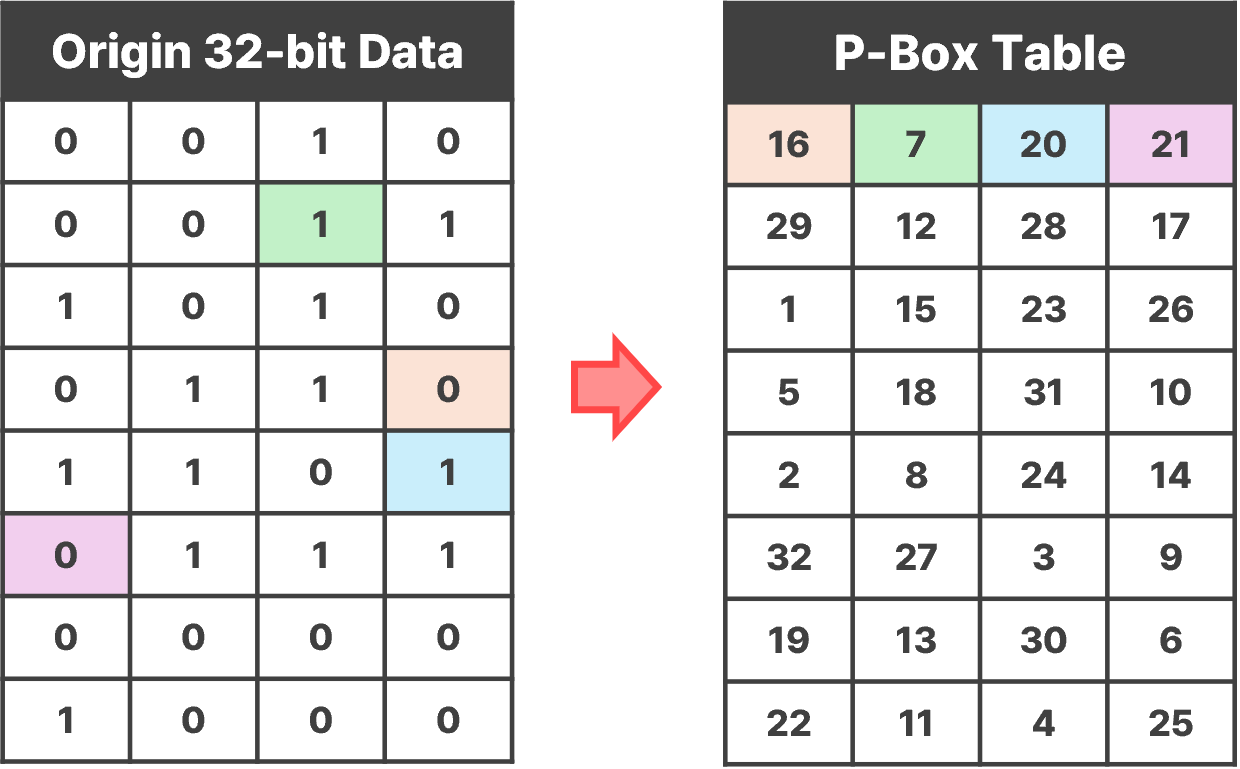
4. P-Box (Permutation Box) 연산

  • 초기 전치와 같은 방법으로, P-Box(고정표)에 기재된 규칙대로 섞음

5. XOR(Exclusive-OR) 연산 with 왼쪽 32비트

6. 원본 오른쪽 32비트 값과 XOR 연산 32비트 합치기

  • 해당 과정을 16 라운드(횟수; 1번 + 15번 추가) 진행함

7. 최종 전치 (Final Permutation)

  • 16 라운드가 끝나면, 최종 전치를 시행함 (모든 비트값의 순서를 바꿈)
    • 1번째 비트 값을 58번째로, 2번째 비트 값을 50번째로 ...
  • 초기 전치를 통해 순서를 바꾼 것들을 원상태로 복구함
    • 복호화가 암호화의 역순이기 때문에, 일관성(대칭성)을 제공하기 위함
  • 즉, 최종 전치는 초기 순열의 역의 관계에 있다고 할 수 있음
    • IP^(-1) = Inverse initial permutaion라고 부르기도 함

키 알고리즘

1. 초기 전치 (Parity Drop)

ℹ️ 패리티 비트 - 전달 받은 정보가 손상되었는지 오류를 검출하는데 사용하는 비트

  • 8비트당 하나씩 존재하는 패리티 비트를 제거함으로서 64비트 → 56비트가 됨
    • 이 과정에서 56비트 순열 테이블(PC-1)을 사용하여 비트 순서를 재배열 함
  • 56비트 키 값은 28비트 씩 절반으로 나누고, 각각 순환 시프트 연산을 수행함

2. 순환 시프트 연산 (Circular Shift)

ℹ️ 시프트(Shift) - 특정 비트 수 만큼 왼쪽이나 오른쪽으로 미는 것

  • 각 라운드마다 왼쪽 방향으로 순환 시프트 연산을 하여 라운드 키를 생성함
  • 단, 1/2/9/16 라운드만 1비트, 그 외의 라운드는 2비트 시프트 연산을 수행함

3. 축약 전치 (Compression P-Box)

  • 각각의 28비트를 결합하여 56비트로(중간 키) 합침
  • 그리고, 56비트 순열 테이블(PC-2)를 이용하여 48비트의 라운드 키를 생성함
    • 초과된 8비트는 버려짐

AES(Advanced Encryption Standard; 고급 암호화 표준)

ℹ️ 대칭 키 암호화 중 블록 암호의 일종으로, 키의 길이에 따라 표준(AES-128/192/256)이 다름

  • 표준 - 숫자는 키의 비트 수를 나타내고, 키 길이가 길수록 보안 강도가 높아짐

핵심 알고리즘 (AES-128 기준)

ℹ️ 해당 알고리즘을 128비트 키는 10번, 192비트 키는 12번, 256비트 키는 14번 반복함 (라운드 수)

1. 키 확장 (Key Expansion)

  • 원래의 암호화 키를 사용하여 각 라운드에 사용될 여러 개의 라운드 키를 생성함

2. 초기 라운드 키 추가 (Initial Round Key Addition)

  • 평문 블록과 첫 번째 라운드 키를 XOR 연산함

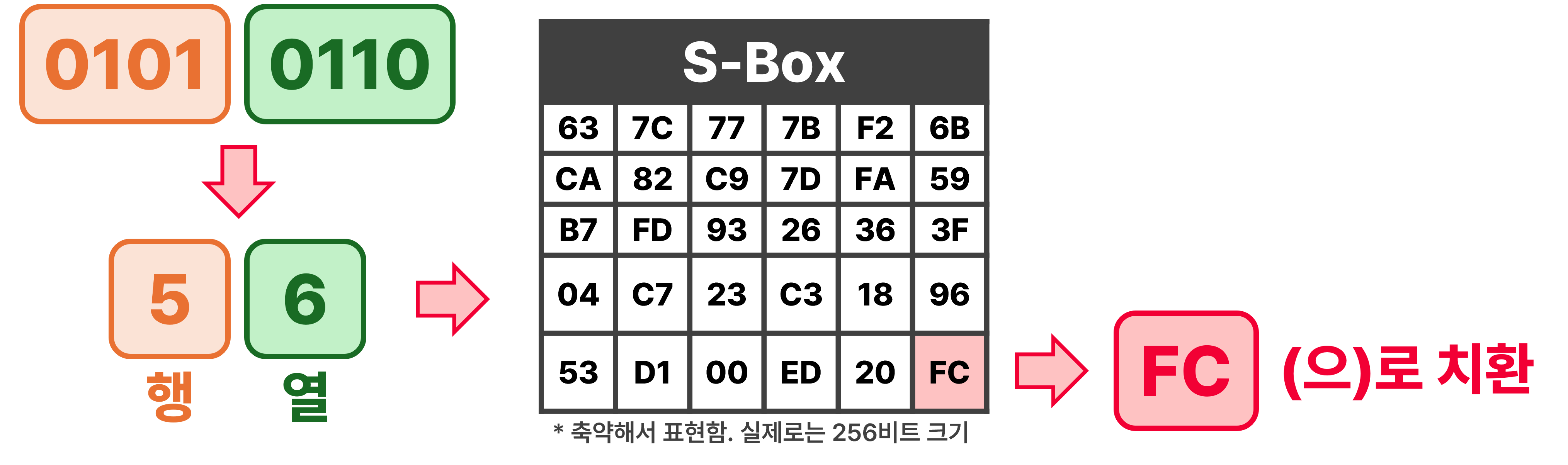
3-1. 바이트 치환 (SubBytes)

  • 각 바이트(8비트)를 4비트씩 나누어 2개의 16진수로 계산 후, 왼쪽 4비트를 S-Box의 행으로, 오른쪽 4비트로 열로 테이블을 읽고 치환함
    • ex. 왼쪽 4비트(0101)와 오른쪽 4비트(0110) -> 5행 6열
  • 해당 과정을 모든 16바이트(128비트)에 대해 독립적으로 수행함

3-2. 행 시프트 (ShiftRows) - 왼쪽으로 순환 시프트

AES에서의 순환 시프트는 DES와 달리 바이트 단위로 이루어지므로, 한 바이트 내에서 비트 순서가 바뀌지 않음

  • 첫 번째 행은 순환 시프트를 하지 않음
  • 두 번째 행은 1바이트 왼쪽으로 순환 시프트를 수행함
  • 세 번째 행은 2바이트 왼쪽으로 순환 시프트를 수행함
  • 네 번째 행은 3바이트 왼쪽으로 순환 시프트를 수행함

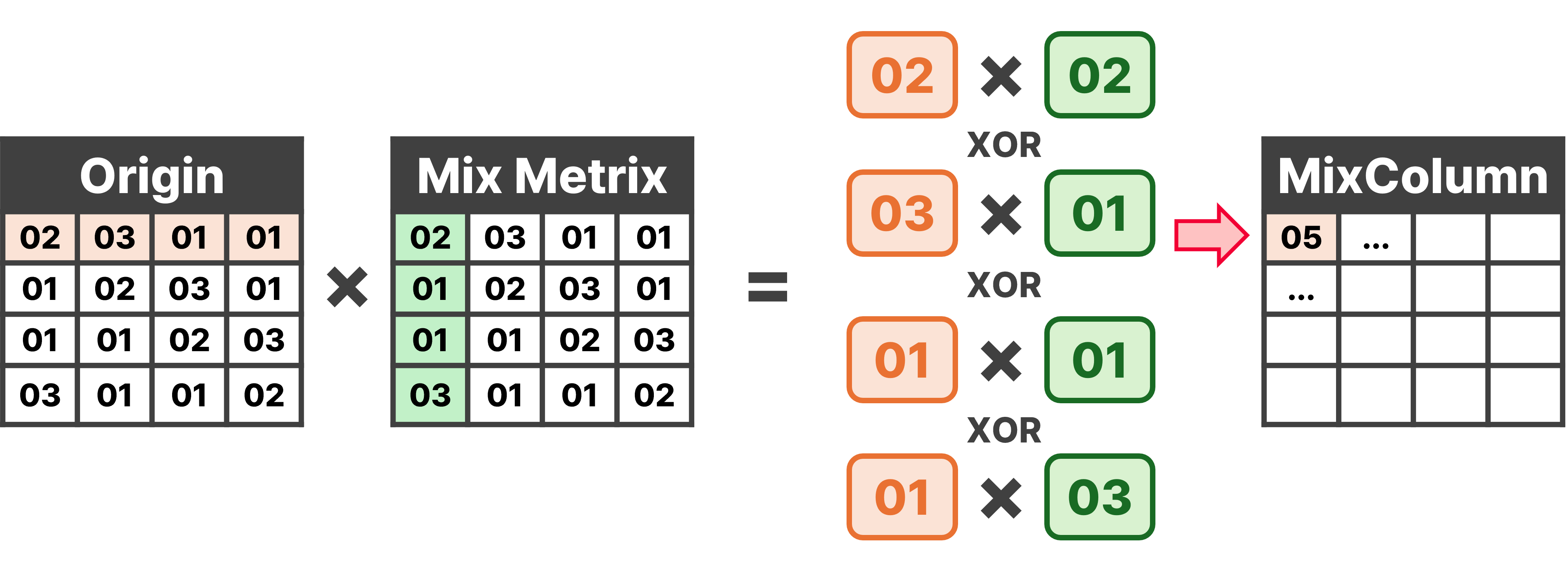
3-3. 열 혼합 (MixColumns) - 단, 마지막 라운드는 제외

  • 16바이트의 행렬(상태 행렬)을 혼합 행렬과 곱하여 상태 행렬을 갱신함

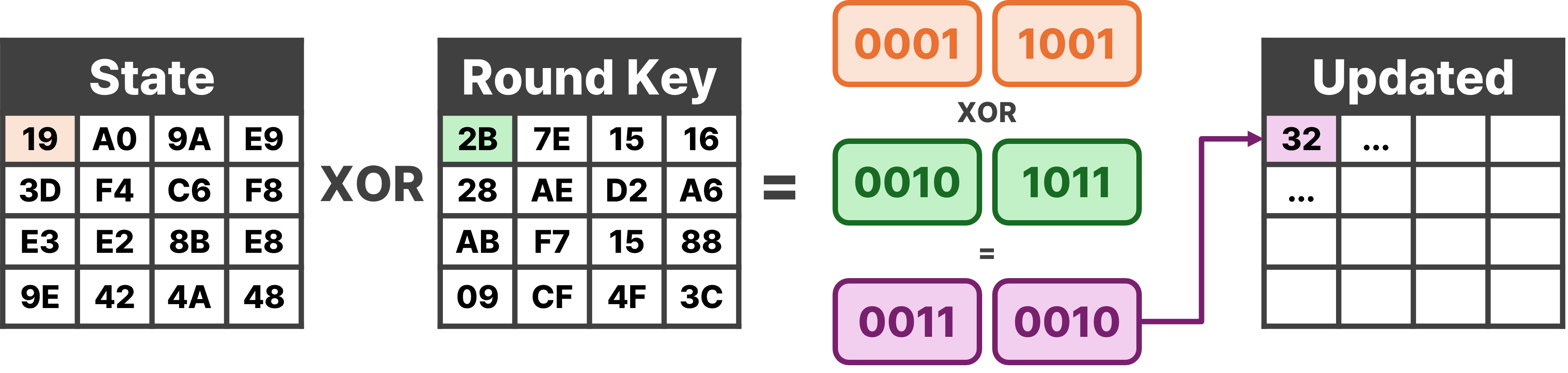
3-4. 라운드 키 추가 (AddRoundKey)

  • 각 상태 행렬의 바이트 값과 해당 라운드의 라운드 키와 XOR 연산을 수행함
  • ex. 상태 행렬 일부 값이 19이고, 라운드 키 일부 값이 2b일 경우
    • 19 XOR 2B = 0001 1001 XOR 0010 1011 = 0011 0010 = 32

CryptoHack

1. INTRODUCTION

1-1. Finding Flags

  • CryptoHack에서 문제를 해결하려면, Flag를 찾아야한다.
  • 이 Flag는 "crypto{...}" 형태로 주어진다.
  • 문제에서 'This Flag'를 제출하라고 하기에, "crypto{y0ur_f1rst_fl4g}"를 제출하면 된다.

1-2. Great Sneak

#!/usr/bin/env python3

import sys
# import this

if sys.version_info.major == 2:
    print("You are running Python 2, which is no longer supported. Please update to Python 3.")

ords = [81, 64, 75, 66, 70, 93, 73, 72, 1, 92, 109, 2, 84, 109, 66, 75, 70, 90, 2, 92, 79]

print("Here is your flag:")
print("".join(chr(o ^ 0x32) for o in ords))
  • Python3가 암호화 스크립트와 공격을 빠르게 하는데 가장 이상적인 프로그래밍 언어라고 한다.
  • 문제에서는 첨부된 Python 파일을 실행하면 플래그를 얻을 수 있다고 한다.
  • 그래서, 'great_snakes.py'를 다운로드하고 실행하면 "crypto{z3n_0f_pyth0n}" 값이 나온다.

2. General - ASCII

question = [99, 114, 121, 112, 116, 111, 123, 65, 83, 67, 73, 73, 
			95, 112, 114, 49, 110, 116, 52, 98, 108, 51, 125]

for element in question:
    print(chr(element), end="")
  • ASCII(이하 아스키코드)는 0~127(2^7개) 정수를 이용해서 텍스트를 표현할 수 있다.
  • 아래 주어진 배열을 사용하여, 각 원소의 값을 ASCII코드로 변환하면 플래그를 얻을 수 있다고 한다.
  • 즉, for 문을 사용하여 각 원소를 ASCII 코드로 변환하는 내장 연산자 'chr'을 사용하여 변환하고 이어서 출력하면, "crypto{ASCII_pr1nt4bl3}" 값이 나온다.

3. RSA

3-1. Modular Exponentiation

print(pow(12, 65537, 17*23))
  • RSA의 모든 연산에는 모듈러 지수가 사용된다고 한다.
  • 예시로 '2^{10} mod 17'가 주어졌는데, 이는 "1024를 17로 나눈 나머지 값"을 의미한다.
  • Python에서 이를 편리하기 연산하기 위해, 'pow(b, e, m)' 내장 연산자가 있다고 한다.
    • b는 base(밑), e는 element(지수), m은 modulus(나누는 값)을 의미한다.
  • 즉, 해당 문제의 플래그를 얻으려면, '101^{17} mod 22663'을 계산하면 된다.
    • 정답은 19906이다.

3-2. Public Keys

print(pow(12, 65537, 17*23))
  • RSA 암호화는 메시지를 지수로 모듈화한 것이다.
  • N(모듈러스)의 값은 일반적으로 두 소수의 곱이라고 한다. (N = P * Q)
  • 그리고, RSA 공개 키는 모듈러스와 지수로 이루어진다. (N, e)
    • 여기서 지수 e는 일반적으로 65537라는 값을 가진다.
  • 즉, 해당 문제의 플래그를 얻으려면, 12를 암호화 해야한다.
    • P가 17, Q가 23인 모듈러스와 e값이 65537을 모듈러 연산을 통해 암호화하면 된다.
    • 정답은 301이다.

4. SYMMETRIC CIPHERS - Keyed Permutations

  • AES는 'Keyed 순열'을 수행한다고 한다.
  • 모든 가능한 입력 블록을 고유한 출력 블록에 매핑하고, 키를 사용하여 어떤 순열을 수행할지 결정한다고 한다.
  • 같은 키를 사용하여 순열을 역으로 수행하면, 출력 블록을 입력 블록으로 다시 매핑할 수 있다고 한다.
  • 즉, 입력 블록과 출력 블록은 일대일 대응 관계가 있는 것이 중요하다고 한다. (없으면 재해독 불가)
  • 문제에서는 "일대일 대응을 나타내는 수학 용어"를 묻고 있다. 정답은 Bijection이다.

새로 알게된 것

암·복호화가 복잡한 알고리즘을 거쳐서 이해하기 어렵다는 것은 알고 있었는데, 실제로 접해보니 말그대로 정말 어려웠다. 어렵긴하지만 대표적인 암호화 알고리즘을 찬찬히 뜯어보니 생각대로 간단한 규칙이 있다는 것이 흥미로웠다. 해당 사항은 DES에 대한 이야기이고, 현재 대중적으로 쓰이는 암호화 방식, 즉 더더욱 복잡한 알고리즘을 가진 AES는 이해하기 힘들었다. 이 점에 대해서는 아직 공부를 거듭할 필요가 있다고 생각되었다.

참고한 자료

profile
한샛코드
개발도 하고 요리도 하는 노근본 개발자
다음 포스트

2주차. CryptoHack, 그리고 Protocol 5.0

0개의 댓글