Likelihood

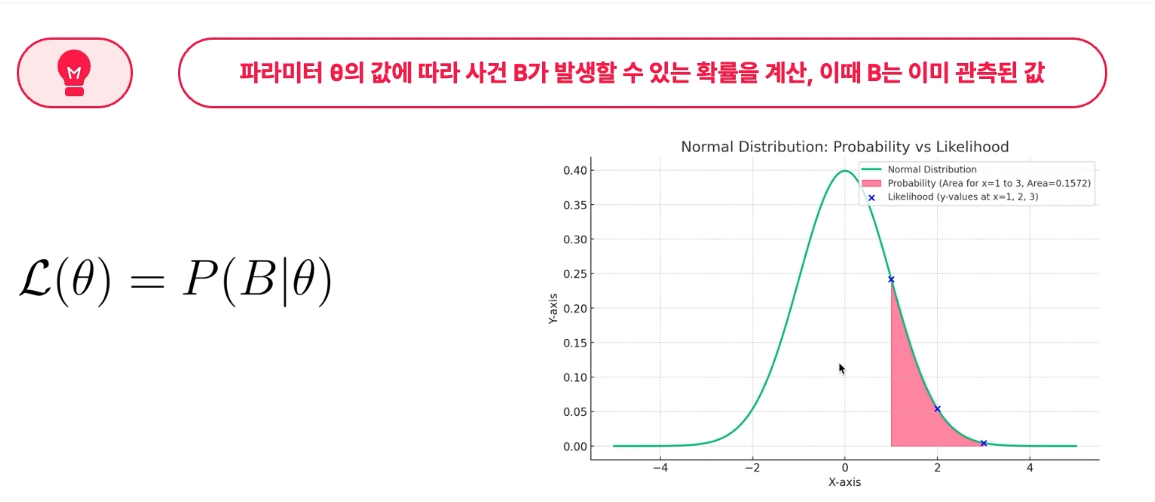
이 식은 likelihood 함수(가능도 함수)를 정의하는 기본적인 수식

구체적으로 설명하면:

• L(θ): Likelihood 함수를 의미합니다. θ(세타)에 대한 함수입니다.
• P(B|θ): 특정 매개변수 θ가 주어졌을 때, 관측된 데이터 B가 발생할 조건부 확률을 의미합니다.

쉬운 예시로 설명해드리면:
🎲 동전 던지기 실험에서,

• B = 관측된 데이터 (예: 앞면이 3번, 뒷면이 7번 나옴)
  • 앞면이 적게 나오는 불공정한 동전
• θ = 동전의 앞면이 나올 확률 (예: θ = 0.5는 공정한 동전)

만약 동전을 10번 던져서 앞면이 3번, 뒷면이 7번 나왔다면:
L(θ) = P(B|θ) = C(10,3) × θ³ × (1-θ)⁷

이때:

• θ = 0.5일 때 likelihood = 10C3 × (0.5)³ × (0.5)⁷ = 0.1172
• θ = 0.3일 때 likelihood = 10C3 × (0.3)³ × (0.7)⁷ = 0.2668

이 경우 θ = 0.3일 때의 likelihood가 더 크므로, 관측된 데이터는 동전이 편향되었을 가능성(θ = 0.3)을 더 강하게 지지합니다.

---

10C3(조합)을 사용하는 이유

10C3은 10개 중 3개를 선택하는 경우의 수로, 이항분포에서 사용되는 계수입니다.

🎯 계산 과정:
10C3 = 10!/(3! × 7!) = 120

왜 필요한가?

• 동전을 10번 던져서 앞면이 3번 나오는 경우, 앞면이 나오는 순서가 여러가지일 수 있습니다.
• 예: (앞,앞,앞,뒤,뒤,뒤,뒤,뒤,뒤,뒤), (앞,뒤,앞,뒤,앞,뒤,뒤,뒤,뒤,뒤) 등

전체 likelihood 수식:
L(θ) = 10C3 × θ³ × (1-θ)⁷

이를 분해하면:
1. 10C3: 10번 중 3번의 앞면이 나오는 모든 가능한 순서 조합
2. θ³: 앞면이 나올 확률의 3승 (앞면 3번)
3. (1-θ)⁷: 뒷면이 나올 확률의 7승 (뒷면 7번)

구체적인 계산 예시:
θ = 0.5일 때,
L(0.5) = 120 × (0.5)³ × (0.5)⁷
= 120 × 0.125 × 0.0078125
= 0.1172

만약 10C3을 곱하지 않는다면:

• 특정한 한 가지 순서의 확률만 계산하게 됨
• 실제로는 같은 결과(앞면 3번, 뒷면 7번)를 만드는 여러 가능한 순서들의 확률을 모두 고려해야 함

이것이 바로 이항분포의 확률질량함수(probability mass function)이며, 일반식은:
P(X=k) = nCk × p^k × (1-p)^(n-k)

• n: 시행 횟수
• k: 성공 횟수
• p: 성공 확률