모델 평가에서의 편향과 분산

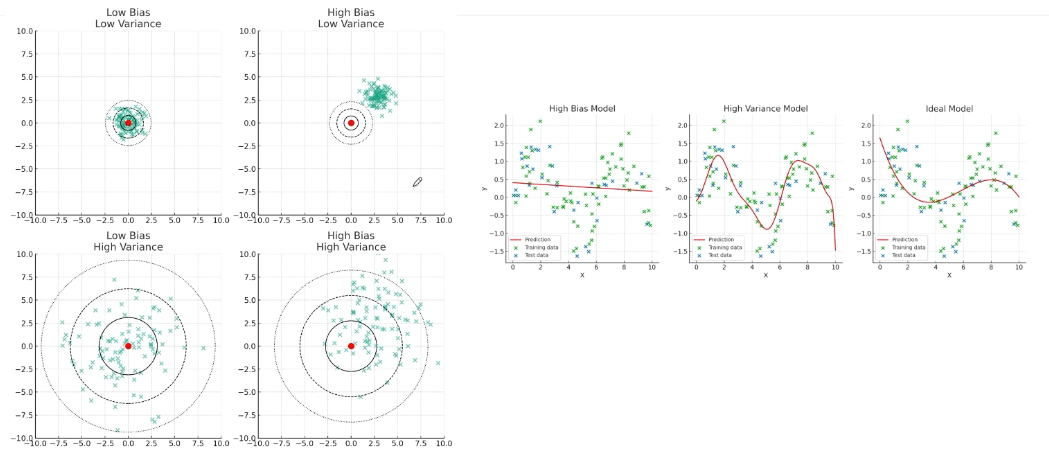
서울 강남의 아파트 가격을 예측하는 모델을 만든다고 합시다.

1. 편향(Bias)

• 정의: 모델의 예측값이 실제값으로부터 얼마나 멀리 떨어져있는지를 나타냅니다
• 높은 편향의 예:

  # 너무 단순한 모델
  가격 = 0.5 * 평수

  이 모델은 평수만 고려하고 다른 중요한 변수들(지하철역과의 거리, 건물 연식, 학군 등)을 무시합니다. 따라서 예측값이 실제값과 큰 차이를 보입니다.

2. 분산(Variance)

• 정의: 다른 데이터셋으로 학습했을 때 모델의 예측값이 얼마나 변동이 심한지를 나타냅니다
• 높은 분산의 예:

  # 너무 복잡한 모델
  가격 = a * 평수³ + b * 평수² + c * 평수 + d * 층수³ + e * 층수² + f * 층수 
      + g * 역세권_점수³ + h * 역세권_점수² + i * 역세권_점수 
      + j * (평수 * 층수 * 역세권_점수)

  이 모델은 너무 많은 고차항을 포함하고 있어서, 학습 데이터의 작은 변화에도 예측값이 크게 달라집니다.

3. 트레이드오프 관계
   실제 강남 아파트 데이터로 예시를 들어보겠습니다:

• 낮은 편향, 높은 분산 모델:

  • 훈련 데이터: 95% 정확도
  • 테스트 데이터: 75% 정확도
  • 특징: 훈련 데이터는 잘 맞추지만, 새로운 데이터에서는 성능이 크게 떨어짐

• 높은 편향, 낮은 분산 모델:

  • 훈련 데이터: 80% 정확도
  • 테스트 데이터: 78% 정확도
  • 특징: 전반적인 성능은 낮지만, 안정적인 예측을 보임

4. 최적의 모델 찾기

# 적절한 복잡도의 모델
가격 = a * 평수 + b * 층수 + c * 역세권_점수 
    + d * (평수 * 역세권_점수) + e * 건물_연식

이 모델은:

• 중요 변수들을 모두 포함
• 적절한 상호작용항 포함
• 불필요한 고차항은 제외

이러한 모델은:

• 훈련 데이터: 88% 정확도
• 테스트 데이터: 86% 정확도
  로 안정적이면서도 높은 성능을 보입니다.

실제 적용할 때의 팁:
1. 교차 검증을 통해 편향과 분산을 모니터링하세요
2. 특성 선택을 신중히 하되, 너무 많은 특성은 피하세요
3. 정규화(Regularization)를 통해 과적합을 방지하세요

---

편향과 분산의 적절한 균형을 찾는 방법

1. 모델 복잡도 조절

• 너무 단순하면: 높은 편향 → 복잡도 증가
• 너무 복잡하면: 높은 분산 → 복잡도 감소

2. 데이터 관련 방법

• 데이터 양 늘리기
  • 더 많은 훈련 데이터 → 분산 감소
  • 양질의 데이터 수집 → 편향 감소
• 특성(Feature) 엔지니어링
  • 중요 특성 추가 → 편향 감소
  • 불필요한 특성 제거 → 분산 감소

3. 학습 과정 조절

• 학습률(Learning Rate) 조정
  • 너무 크면 → 높은 분산
  • 너무 작으면 → 높은 편향
• 조기 종료(Early Stopping)
  • 과적합 전에 학습 중단 → 분산 감소

4. 규제화(Regularization) 적용

• L1 규제: 불필요한 특성 제거
• L2 규제: 가중치 크기 제한
  → 둘 다 분산을 감소시키는 효과

5. 실제 적용 예시: 주택가격 예측

• 초기상태: 높은 분산

  • 증상: 테스트 데이터에서 예측이 불안정
  • 해결: 특성 수 줄이기, 규제화 적용

• 초기상태: 높은 편향

  • 증상: 전반적으로 예측이 부정확
  • 해결: 중요 특성 추가, 모델 복잡도 증가

6. 균형 찾기 위한 체크리스트

• 훈련 오차 vs 검증 오차 모니터링
• 교차 검증 수행
• 학습 곡선 관찰
• 특성 중요도 분석

7. 경험적 조언

• 처음에는 단순 모델로 시작
• 점진적으로 복잡도 증가
• 각 변경의 영향 측정
• 검증 데이터셋 활용

이런 방법들을 상황에 맞게 조합하여 사용하면 좋은 균형을 찾을 수 있습니다. 특히 중요한 것은 점진적인 접근과 각 변경사항의 효과를 측정하는 것입니다.