Sorting Algorithm
1. Bubble Sort
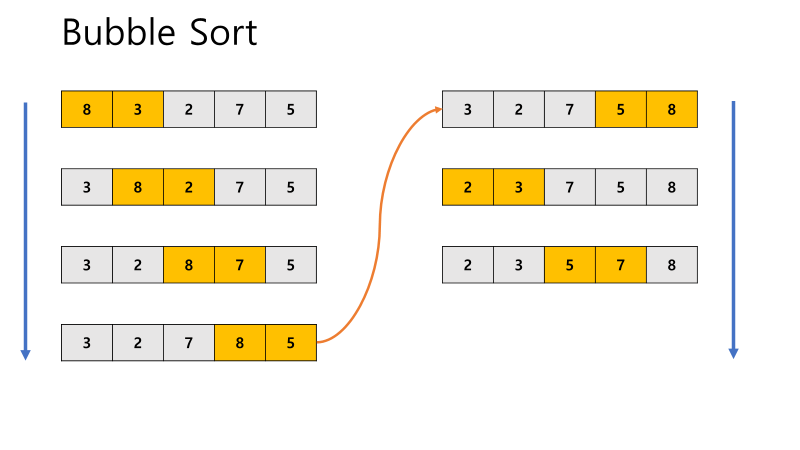
- 인접한 두 개의 데이터를 비교하며 정렬하는 방법
- 특징
- 장점 : 구현이 매우 간단하다.
- 단점
- 하나의 요소가 가장 왼쪽에서 가장 오른쪽으로 이동하기 위해서는 배열의 모든 요소들과 교환되어야만 한다.
- 특정 요소가 최종 정렬 위치에 이미 있는 경우라도 교환되는 일이 일어난다. - 자료의 교환 작업(swap)이 이동 작업(move)보다 더 복잡하기 때문에 단순함에도 불구하고 거의 쓰이지 않는다.
- 시간 복잡도 : O(n^2)
2. Selection Sort
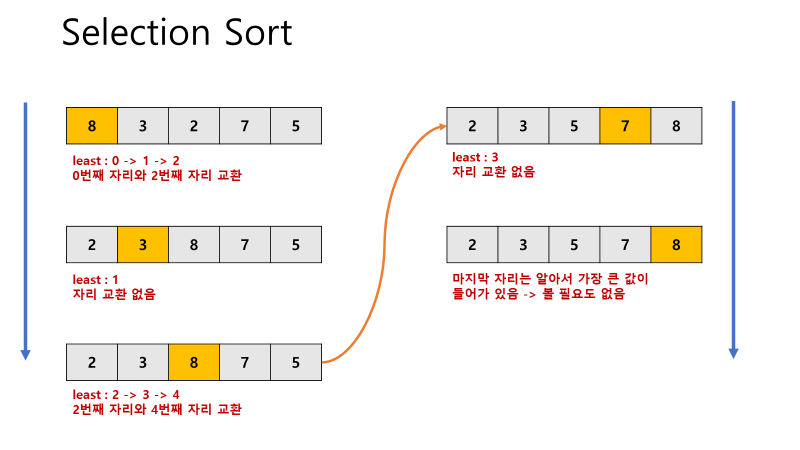
- 해당 순서에 원소를 넣을 위치는 이미 정해져 있고, 어떤 원소를 넣을지 선택하는 알고리즘
- 특징
- 장점 : 자료 이동 횟수가 미리 결정된다.
- 단점
- 값이 같은 레코드가 있는 경우에 상대적인 위치가 변경될 수 있다. - 시간 복잡도 : O(n^2)
3. Insertion Sort
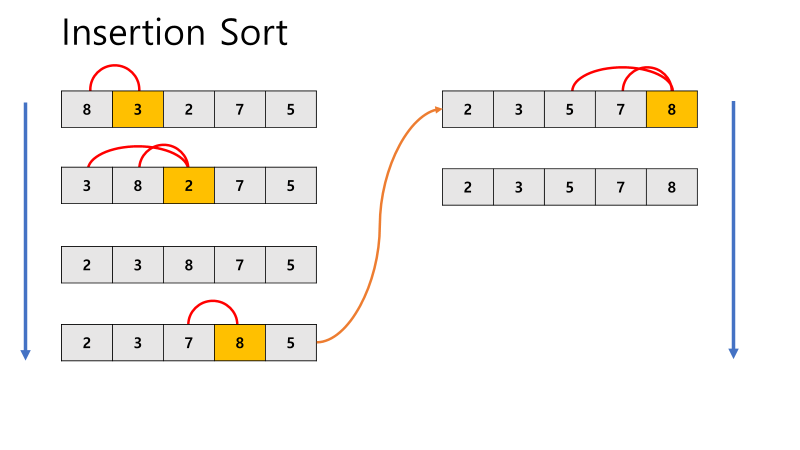
- i번째 원소를 검사할 때 i-1번째부터 0번째까지 비교하며 i번째가 더 작다면 이동하려는 곳부터 i-1까지의 값들을 한 칸씩 뒤로 밀고 해당 인덱스에 i번째 값 삽입
- 특징
- 장점
- 정렬하고자 하는 배열의 길이가 적을 경우 알고리즘 자체가 매우 간단하므로 다른 복잡한 정렬 방법보다 유리할 수 있음
- 대부분의 레코드가 이미 정렬되어있는 경우 매우 효율적일 수 있음 - 단점
- 비교적 많은 이동 필요
- 길이가 긴 경우 적합하지 않음 - 시간 복잡도 : O(n^2)
- 장점
4. Merge Sort
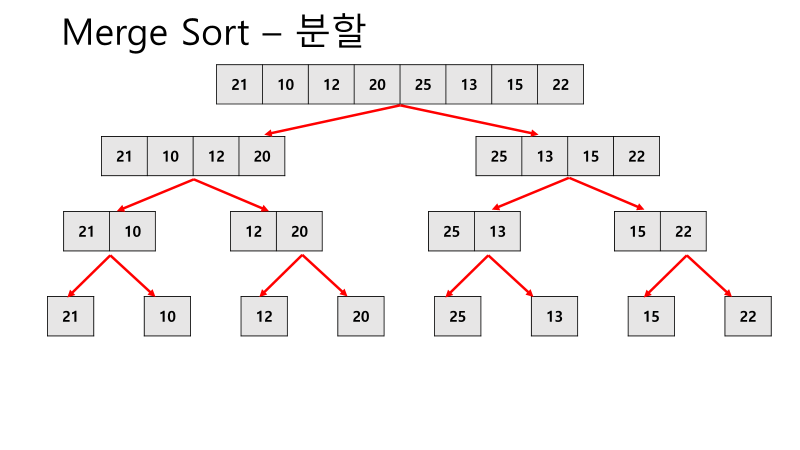
- 배열의 크기를 작은 단위로 나누어 배열의 크기를 줄이는 원리 사용
- Divide and Conquer 사용하여 반씩 분할하다가 자기 자신만 남을 때(즉, 사이즈가 1일 때) 비교를 시작한다
- 임시 배열에 저장하고, 저장된 순서를 합친 값으로 반환한다
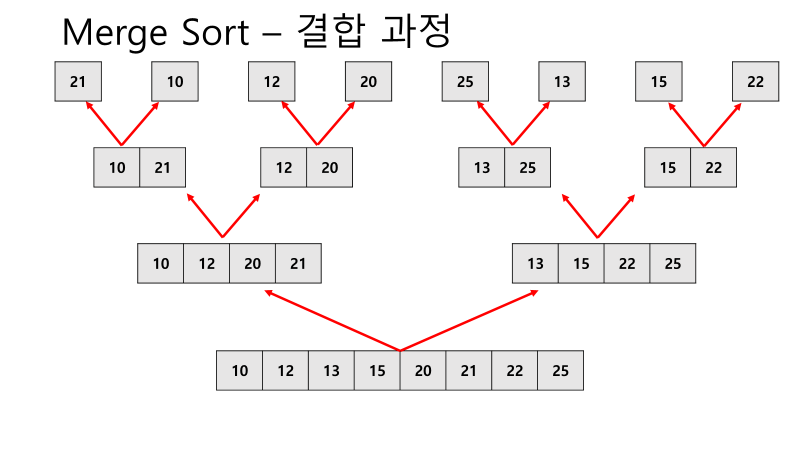
- 특징
- 장점
- 데이터의 분포에 영향을 덜 받는다. 즉, 입력 데이터가 무엇이든 간에 정렬되는 시간 동일하다.
- 만약 LinkedList로 구성 시, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다
- 따라서 크기가 큰 레코드를 정렬할 경우에 연결 리스트 사용시, 머지소트는 다른 어떤 정렬 방법보다 효율적이다 - 단점
- 배열로 구성하면, 임시 배열이 필요하다
- 레코드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비를 초래한다. - 시간 복잡도 : O(nlogn)
- 장점
** 코드 참고
블로그 - Java로 구현하는 쉬운 Merge Sort
Merge Sort - java 코드
5. Heap Sort
- 최대 힙 트리(내림차순 정렬)나 최소 힙 트리(오름차순 정렬)를 구성해 정렬하는 방법
- 완전 이진 트리 형태로 만든 후 하나씩 요소를 힙에서 꺼내어 배열의 뒤부터 저장
- 삭제되는 요소들(최댓값부터 삭제)은 값이 감소되는 순서로 정렬되게 됨
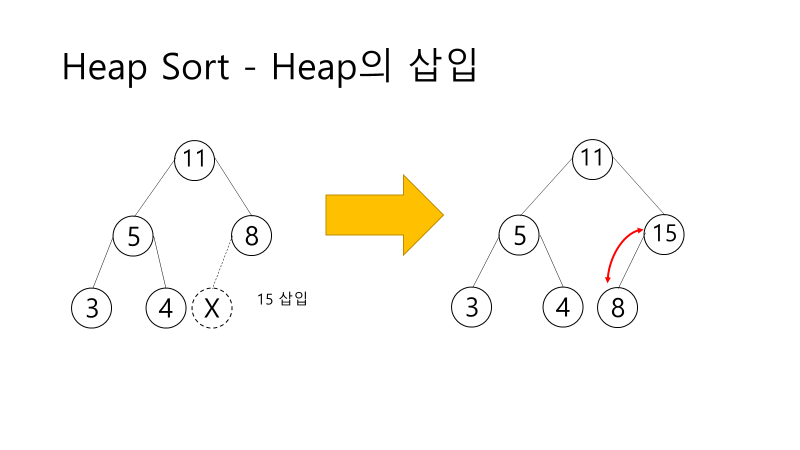
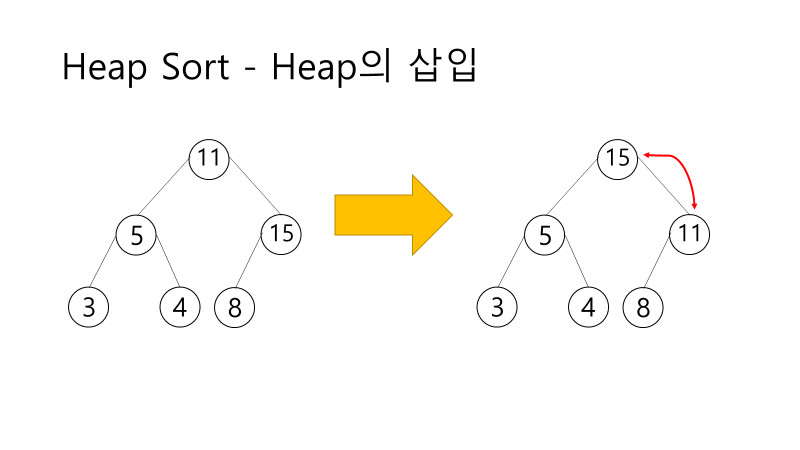
- 특징
- 장점
- 시간 복잡도가 좋은 편
- 힙 정렬이 가장 유용한 경우는 전체 자료를 정렬하는 것이 아니라 가장 큰 값 몇개만 필요할 경우이다. - 시간 복잡도 : O(nlogn)
- 장점
6. Quick Sort
- pivot을 이용하여 partition 한다.
- 오름차순 정렬 시, pivot을 기준으로 왼쪽은 pivot의 값보다 작은 값이, 오른쪽은 큰 값이 오도록 한다.
- 분할된 부분 리스트에 대하여 순환 호출을 이용하여 정렬을 반복한다.
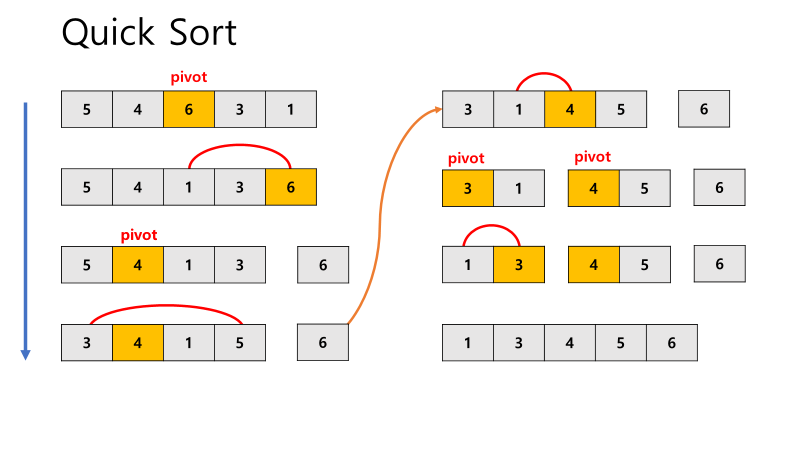
- 특징
- 장점
- 속도가 빠르다
- 추가 메모리 공간을 필요로 하지 않는다. - 단점
- 정렬된 리스트에 대해서는 퀵 정렬의 불균형 분할에 의해 오히려 수행시간이 더 많이 걸린다 - 불균형 분할을 방지하기 위하여 피벗을 선택할 때 더욱 리스트를 균등하게 분할할 수 있는 데이터를 선택한다.
(ex. 몇개의 데이터 중에서 크기순으로 중간값을 피벗으로 선택) - 시간 복잡도 : 최악 - O(n^2), 평균 - O(nlogn)
Quick Sort - java 코드
- 장점
