Java와 Spring 공부를 시작하면서, 기존 기술 스택인 Python과 Django와의 공통점, 차이점, 특징 등을 정리하기 위해 Java vs Python 시리즈를 시작합니다.

컴퓨터의 소수 표현은 왜 부정확할까?

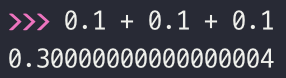
Java와 Python에서 0.1 + 0.1 + 0.1 을 계산한 결과. 둘 다 정확하게 0.3 이 나오지 않는다.

Java와 Python 뿐 아니라 대부분의 프로그래밍 언어에서 0.1 + 0.1 + 0.1 을 계산하면 0.3 이 아닌 0.30000000000000004 와 같은 부정확한 값이 나옵니다. 왜 그럴까요?

컴퓨터는 숫자를 이진법을 사용하여 저장합니다. 이진법에서는 소수를 정확하게 표현하기 어려운 경우가 많은데, 예를 들어 십진법으로 정확하게 표현되는 0.1 의 경우 이진법으로 변환하면 무한 소수로 나타납니다.

0.1 (10진법) = 0.000110011001100110011001100110011...(2진법)

컴퓨터는 숫자를 저장하는 데 사용하는 메모리가 한정되어 있습니다. 소수를 표현하는 방법 중 주로 쓰이는 부동소수점(floating point) 방식은 일반적으로 IEEE 754를 따르고, 이는 일반적으로 32비트 또는 64비트로 소수를 저장합니다. 각각 Java에서 float, double에 해당하는 방식입니다. (float의 이름이 어디서 왔는지를 짐작할 수 있는 부분입니다.)

메모리가 한정되어 있기 때문에, 무한 소수는 값을 정확하게 저장하지 못하고 근사값으로 저장합니다. 근사값으로 저장하는 과정에서 일정 크기 이하의 숫자는 버리거나 반올림하게 되고, 이로 인해 오차가 발생합니다. 이렇게 발생한 오차는 이후 계산에서 누적되어 일정 크기 이상이 되면 0.30000000000000004 와 같은 형태로 드러납니다.

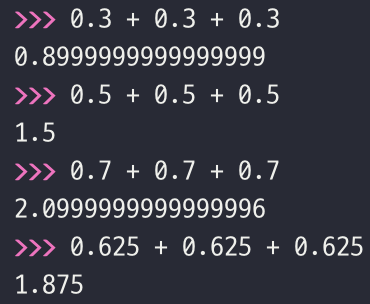
이진법으로 무한 소수인 0.3, 0.7의 경우에도 오차가 발생한다. 이진법으로 유한 소수인 0.5, 0.625의 경우 정확하게 표현된다.

어떻게 해결할 수 있을까?

정수 연산 사용

십진법으로 표현된 소수는 이진법으로 저장 시 무한 소수로 표현되는 것이 문제입니다. 그렇다면 십진법으로 표현된 정수는? 무조건 유한한 자릿수로 표현할 수 있습니다. 그러므로 소수에 10의 거듭제곱을 곱해 정수로 만든 후 계산한다면 이 문제를 해결할 수 있습니다.

0.1 에 100을 곱해 계산한 뒤 100으로 나누어 정확한 결과를 출력했다.

하지만 이 경우 소수의 자릿수에 따라 곱해야 하는 수를 직접 정해줘야 하는 문제가 있습니다. 간단한 알고리즘 문제 정도에는 적용할 수 있겠지만, 어떤 소수에나 전부 적용되게 만들기는 복잡합니다.

라이브러리 사용

Java의 BigDecimal, Python의 decimal.Decimal 과 같은 라이브러리를 사용하면, 소수를 정확하게 표현하고 연산할 수 있습니다.

Java

import java.math.BigDecimal;

BigDecimal a = new BigDecimal("0.1");
BigDecimal result = a.add(a).add(a);
System.out.println(result);  // 0.3

Python

from decimal import Decimal

result = Decimal('0.1') + Decimal('0.1') + Decimal('0.1')
print(result)  # 0.3

이 라이브러리들은 어떻게 소수를 정확하게 연산할 수 있을까요? 앞서 다루었던 컴퓨터에서 소수 표현이 부정확한 이유는, 이진법으로 소수를 저장하여 무한 소수가 발생하기 때문입니다.

라이브러리들의 이름(decimal, 십진법)에서 알 수 있듯이, 이 라이브러리들은 십진법 기반의 내부 표현을 사용하여 정확한 숫자 값을 저장합니다. 0.1 과 같은 숫자가 십진법 그대로 저장되기 때문에, 변환 오차 없이 연산이 가능합니다.

라이브러리 분석

십진법 기반의 내부 표현이 무엇을 말하는 것인지 궁금해져서, python의 decimal 모듈 내부 코드를 확인하면서 자세히 알아보았습니다. 결론부터 말하자면, 위에 언급했던 정수 연산을 패턴화했다고 볼 수 있었습니다.

# _decimal.pyi

class DecimalTuple(NamedTuple):
    sign: int
    digits: tuple[int, ...]
    exponent: int | Literal["n", "N", "F"]

decimal 모듈의 Decimal 객체는 숫자를 받으면 sign, digits, exponent 세 개의 변수로 값을 저장합니다. sign은 수의 부호를, digits는 각 자리 숫자를, exponent는 소수점의 위치를 나타냅니다. 예시를 들어서 설명하겠습니다.

from decimal import Decimal

decimal_value = Decimal("123.45")
decimal_tuple = decimal_value.as_tuple()
print(f"{decimal_value}: {decimal_tuple}")
# 123.45: DecimalTuple(sign=0, digits=(1, 2, 3, 4, 5), exponent=-2)

sign이 0이면 양수, 1이면 음수를 의미합니다. digits는 각 자리를 구성하는 숫자들이 tuple 자료형으로 저장됩니다. exponent는 소수점의 위치를 나타내는데, 여기서는 소수점 아래 둘째 자리까지 있으니 -2가 됩니다.

decimal_value = Decimal("-123.45")
decimal_tuple = decimal_value.as_tuple()
print(f"{decimal_value}: {decimal_tuple}")
# -123.45: DecimalTuple(sign=1, digits=(1, 2, 3, 4, 5), exponent=-2)

-123.45는 sign이 1로 저장되는 것을 볼 수 있습니다.

decimal_value = Decimal("1234500")
decimal_tuple = decimal_value.as_tuple()
print(f"{decimal_value}: {decimal_tuple}")
# 1234500: DecimalTuple(sign=0, digits=(1, 2, 3, 4, 5, 0, 0), exponent=0)

1234500은 뒤의 두 자리가 0이지만, digits에 0이 들어가고 exponent는 2가 아닌 0인 걸 확인할 수 있습니다. 뒤에 들어간 0이 자릿수를 나타내는 것이 아니라 유효숫자이기 때문입니다.

decimal_value = Decimal((0, (1, 2, 3, 4, 5), 2))
decimal_tuple = decimal_value.as_tuple()
print(f"{decimal_value}: {decimal_tuple}")
# 1.2345E+6: DecimalTuple(sign=0, digits=(1, 2, 3, 4, 5), exponent=2)

Decimal에 문자열이 아닌 tuple 자료형을 직접 입력할 수도 있습니다. exponent에 2를 넣어서 확인한 결과, 1.2345E+6처럼 유효숫자 + 자릿수 형태의 수가 된다는 것을 볼 수 있습니다.

정수 연산이 기본값이 아닌 이유는?

정리하면서 이런 의문이 생겼습니다.

decimal과 같은 라이브러리를 굳이 사용하지 않고, 프로그래밍 언어 자체에서 소수를 십진법 정수 연산으로 계산하도록 하면 항상 정확하게 수를 계산할 수 있지 않을까?

그렇게 하지 않는 이유는 처리 속도에 있습니다.

처리 속도 비교

from decimal import Decimal
from datetime import datetime

value = 0
start = datetime.now()
for i in range(10_000_000):
    value += 0.1
end = datetime.now()
print(value)
print(f"Time taken: {end - start}")

# 999999.9998389754
# Time taken: 0:00:00.616951

value2 = Decimal("0")
start2 = datetime.now()
for i in range(10_000_000):
    value2 += Decimal("0.1")
end2 = datetime.now()
print(value2)
print(f"Time taken: {end2 - start2}")

# 1000000.0
# Time taken: 0:00:02.554312

0.1을 1천만 번 더하는 연산을 각각 수행하여 처리 시간을 비교해 보았습니다.

라이브러리 없이 수행했을 때는 결과가 부정확하지만, 처리 시간은 약 0.6초 내외로 측정됩니다.

반면 decimal 모듈을 사용해서 수행했을 때는 결과가 정확하지만, 처리 시간은 약 2.5초 내외로, 약 4배 이상 소요됨을 알 수 있었습니다.

# _pydecimal.py

    def __add__(self, other, context=None):
        ...
        exp = min(self._exp, other._exp)
        ...
        if op1.sign != op2.sign:
            # Equal and opposite
            if op1.int == op2.int:
                ans = _dec_from_triple(negativezero, '0', exp)
                ans = ans._fix(context)
                return ans
        ...
        if op2.sign == 0:
            result.int = op1.int + op2.int
        else:
            result.int = op1.int - op2.int

        result.exp = op1.exp
        ans = Decimal(result)
        ans = ans._fix(context)
        return ans

_pydecimal.py의 __add__ 메서드를 보면, Decimal 객체의 sign, digits, exponent로 구분되는 부분을 각각 처리하는 로직이 꽤 길게 들어가 있고, 그 후에 숫자들끼리 덧셈을 하는 과정이 수행됩니다.

복잡한 로직 없이 이진수 덧셈만 수행하면 되는 기존 방식보다 시간이 더 오래 걸릴 수밖에 없다는 것을 알 수 있습니다.

기본 연산이 유리한 경우

모든 프로그램이 정확한 수 계산을 요구하는 것은 아닙니다. 물론 정확할수록 좋겠지만, 정확성보다 속도에 우선순위를 두는 경우도 있습니다.

금융 프로그램처럼 한 치의 오차도 없는 정확한 계산이 필요한 경우도 있는 반면, 머신러닝처럼 정확한 계산보다는 빠른 속도를 우선시하는 경우도 있습니다.

근삿값을 사용해도 되는 경우라면 라이브러리를 사용하는 것보다 내장된 기본 연산을 사용하는 것이 더 빠르고 간편할 수 있습니다.

사용 시에 주의해야할 점

Java의 BigDecimal과 Python의 decimal.Decimal에서 정확한 연산을 위해 공통적으로 주의해야 할 점이 있습니다. 바로 숫자를 문자열로 넣어줘야 한다는 점입니다.

Java

import java.math.BigDecimal;

BigDecimal double_value = new BigDecimal(0.1);
System.out.println(double_value);
// 0.1000000000000000055511151231257827021181583404541015625

BigDecimal string_value = new BigDecimal("0.1");
System.out.println(string_value); 
// 0.1

Python

from decimal import Decimal

double_value = Decimal(0.1)
print(double_value)
# 0.1000000000000000055511151231257827021181583404541015625

string_value = Decimal("0.1")
print(string_value)
# 0.1

문자열이 아닌 double 형태로 숫자를 전달할 경우, BigDecimal/decimal 에서는 해당 값을 십진법 정수 형태로 저장하지 않고, 전달받은 소수의 근삿값을 그대로 저장합니다. 정확한 소수 연산을 위해 모듈을 사용한다면 문자열로 숫자 값을 전달해야 합니다.

정리

Java의 기본 자료형을 다루는 강의에서 BigDecimal에 대해 알 수 있었고, 과거 Django 프로젝트를 진행할 때 결제, 정산 등에 사용했던 decimal 모듈과 많은 공통점이 있다고 느껴서 이렇게 포스트로 정리해 보았습니다.

이전에 decimal 모듈을 사용할 때는 단순히 사용법만 익혀서 사용했었는데, 이번에 포스트를 작성하면서 decimal 모듈의 공식 문서도 자세히 읽어보고, 직접 내부 코드를 보면서 어떤 원리로 숫자를 정확하게 저장하는지를 확인했던 것이 기억에 남습니다. 생각보다 공식 문서가 자세히 나와있기도 했구요.

앞으로도 Java와 Python에서 공통적으로 사용하는 개념을 알게 된다면 이렇게 하나 씩 포스트로 정리할 예정입니다.

https://0.30000000000000004.com
자료를 찾아보다가 발견한 사이트, 아예 계산 결과가 도메인이다.
다양한 프로그래밍 언어에서의 0.1 + 0.2 계산 결과를 보여준다.

https://docs.python.org/ko/3.8/library/decimal.html
python decimal 모듈 공식 문서