이진 탐색트리
먼저 트리(tree)와 이진트리(binary tree)를 보자
트리
트리는 그 모양이 뒤집어 놓은 나무와 비슷하다고 해서 이런 이름이 붙었다.
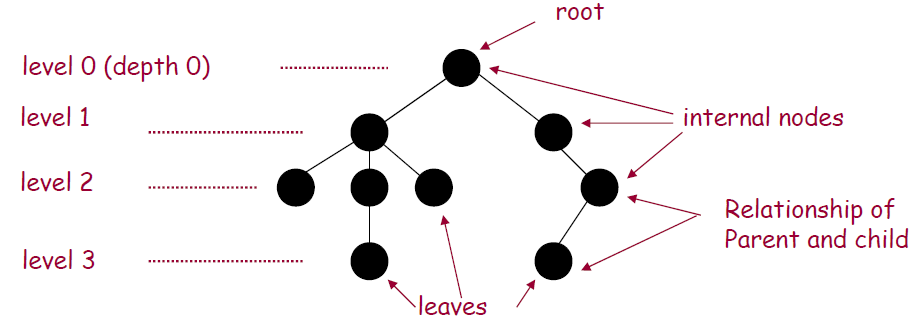
- 노드 : 각각의 검정색 동그라미들, 보통 데이터가 담긴다.
- 엣지 : 노드와 노드사이를 이어주는 선
- 경로 : 인접한 노드들로 이뤄진 시퀀스, 경로의 길이는 경로에 속한 엣지의 수로 나타낸다.
- 높이 : 루트 노드에서 말단 노드에 이르는 가장 긴 경로의 엣지수를 말한다. 특정 깊이를 가지는 노드들의 집합을 레벨이라고 부른다.
- 잎새노드 : 자식노드가 없는 노드를 말한다. internal node는 잎새노드를 제외한 노드를 나타낸다. 루트 노드는 부모 노드가 없는 노드를 말한다.
- 트리의 속성중 가장 중요한 것은 루트노드를 제외한 모든 노드는 단 하나의 부모노드만을 가진다는 것이다.
트리의 성질 및 특징
루트노드를 제외한 모든 노드는 단 하나의 부모노드만을 가짐으로 나오는 트리의 성질및 특징을 알아보자
- 그래프의 한 종류 이다. '최소연결 트리'라고도 불린다.
- 트리는 계층 모델이다.
- 임의의 노드에서 다른 노드로 가는 경로는 유일하다
- 회로(cycle)가 존재하지 않는다.
- 모든 노드는 서로 연결되어 있다.
- 엣지를 하나 자르면 트리가 두개로 분리된다.
- 엣지의 수는 노드의 수에서 1을 뺀것과 같다. (엣지 = 노드 - 1)
이진트리란?
이진트리란 자식노드가 최대 두 개인 노드들로 구성된 트리이다. 이진트리에는 정이진트리, 완전이진트리, 균형이진트리 등이 있다.
-
정이진트리 : 모든 레벨에서 노드들이 꽉 채워진(잎새 노드를 제외한 모든 노드가 자식노드를 2개 가짐)이진트리 이다.
- 레벨에 따른 노드의 숫자는 : level = k , 노드수 = 2^( k + 1) -1
-
완전이진트리 : 마지막 레벨을 제외한 모든 레벨에서 노드들이 꽉 채워진 이진트리
-
정이진트리와 완전 이진트리는 1차원 배열로도 표현이 가능하다.
-
어떤 노드의 인덱스를 index, 왼쪽 자식노드의 인덱스를 left_index, 오른쪽 자식노드의 인덱스를 right_index로 선언하면
left_index = 2 * index + 1
right_index = 2 * index + 2
- 균형이진트리: 모든 잎새노드의 깊이 차이가 많아야 1인 트리를 말한다. 예측가능한 깊이를 가지며, 노드가 n 개인 군형이진트리의 깊이는 logn을 내림한 값이 된다,
트리 순회?? (tree traversal)
트리 순회란 트리의 각 노드를 체계적인 방법으로 방문하는 과정을 말한다. 하나도 빠뜨리지 않고 , 정확히 한번만 중복없이 방문해야한다.
노드를 방문 하는 순서에 따라 전위순회(preorder), 중위순회(inorder), 후위순회(postorder)세가지로 나뉜다.
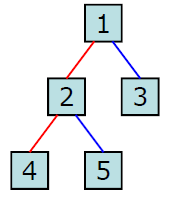
- preorder : 루트 노드에서 시작해서 노드 -> 왼쪽 서브트리 -> 오른쪽 서브트리 순으로 순회하는 방식. 깊이 우선순회(depth-first-traversal) 라고도 한다.
- 1 -> 2 -> 4 -> 5 -> 3 - inorder : 루트노드에서 시작해서 왼쪽 서브트리노드 -> 오른쪽 서브트리 순으로 순회하는 방식. 대칭 순회(symmetric traversal)이라고도 불린다.
- 4 -> 2 -> 5 -> 1 -> 3 - postorder : 루트 노드에서 시작해서 왼쪽 서브트리 -> 오른쪽 서브트리 -> 노드 순으로 순회하는 방식
- 4 -> 5 -> 2 -> 3 -> 1
이진 탐색트리란?
이진탐색과 연결리스트(linked list) 를 결합한 자료구조의 일종이다.
이진탐색의 효율적인 탐색 능력을 유지하면서도, 빈번한 자료 입력과 삭제를 가능하게끔 고안됐다.
예를들면 이진탐색의 경우 탐색에 소요되는 계산복잡성은 O(logN)으로 빠르지만 자료입력이나 삭제가 불가능하다.
연결 리스트의 경우 자료입력, 삭제에 필요한 계산 복잡성은 O(1)로 효율적이지만 탐색하는 데에는 O(n)의 계산 복잡성이 발생한다. 이 두개의 장점을 살려보는 것이 이진 탐색트리의 목적이라고 할 수 있다.
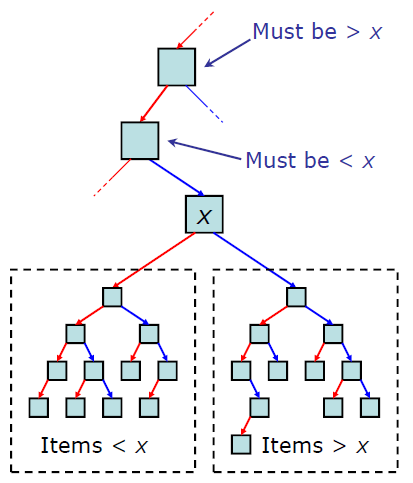
속성
-
각 노드의 왼쪽 서브트리에는 해당 노드의 값보다 작은 값을 지닌 노드들로 이루어져 있다.
-
각 노드의 오른쪽 서브트리에는 해당 노드의 값보다 큰 값을 지닌 노드들로 이루어져 있다.
-
중복된 노드가 없어야 한다.
-
왼쪽 서브트리, 오른쪽 서브트리 또한 이진 탐색트리이다.
-
이진 탐색트리를 순회할 때에는 중위순회(inorder)방식을 사용한다.
- 왼쪽 서브트리 -> 노드 -> 오른쪽 서브트리 순으로
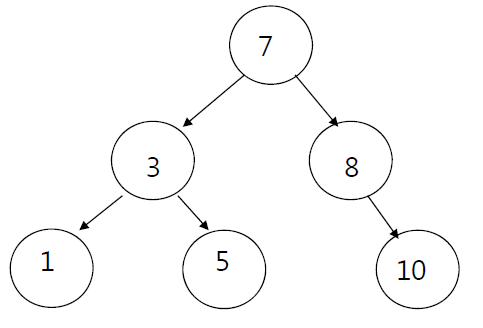
-
위의 그림에서 중위순회를 사용한다면, 순서는 1, 3, 5, 7, 8, 10 순서로 순회한다.
작동
이진탐색트리의 핵심 연산은 검색(retreive), 삽입(insert), 삭제(delete) 이 세가지 이다. 이밖에 생성(create), 이진탐색트리 삭제(destroy), 해당 이진 탐색 트리가 비어 있는지 확인(isEmpty), 트리순회(tree traversal)의 연산들이 있다.
