퀵정렬

개념

 

• 찰스 앤터니 리처드 호어라는 사람이 갭라한 정렬 알고리즘
• 퀵 정렬은 불안정 정렬에 속하며, 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속한다.
• 분할 정복 알고리즘의 하나로, 평균적으로 매우 빠른 수행속도를 자랑하는 정렬 방법
  - 병합정렬과 달리 퀵정렬은 리스트를 비균등하게 분할한다.
  
  
  
  
  
  
• 과정 설명
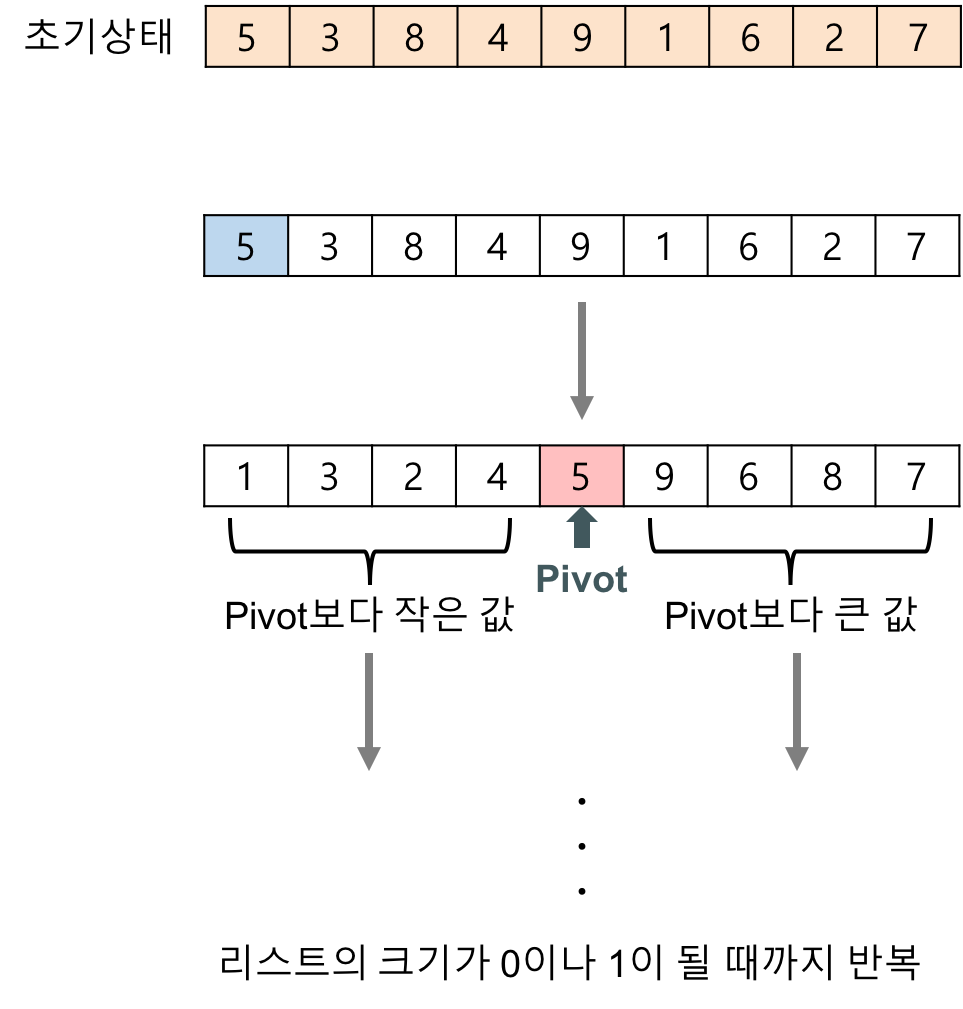
• 리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 피벗(pivot)이라고 한다.
• 피벗을 기준으로 비펏보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다. (피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 피벗을 중심으로 오른쪽: 피벗보다 큰요소들)
• 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
  • 분할된 부분 리스트에 대하여 순환 호출을 이용하여 정렬을 반복한다.
  • 부분 리스트에서도 다시 피벗을 정하고 피벗을 기준으로 2개의 부분 리스트로 나누는 과정을 반복한다.
• 부분 리스트들이 더이상 분할이 불가능할 때까지 반복한다.
  - 리스트의 크기가 0이나 1이 될때까지 반복
  
  
  
  
• 분할 정복 (divide and conquer) 방법
  • 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략.
  • 분할 정복 방법은 대개 순환 호출을 이용하여 구현한다.
  • 분할 : 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분배열로 분할한다.
  • 정복 : 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 방법을 적용한다.
  • 결합 : 정렬된 부분배열들을 하나의 배열에 합병한다.
  • 순환 호출이 한번 진행될 때마다 최소한 하나의 원소(피벗)는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것이 보장된다.
    
    
    
    
    
    
    
    

퀵정렬 알고리즘의 특징

• 장점
  - 속도가 빠르다
  - 시간 복잡도가 O(nlogn)을 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
  • 추가 메모리 공간을 필요로 하지 않는다.
    • 퀵정렬은 O(logn)만큼의 메모리를 필요로 한다.
• 단점
  - 정렬된 리스트에 대해서는 퀵정렬의 불균형 분할에 의해 오히려 수행시간이 더 많이 걸린다.
  • 퀵정렬의 불균형 분할을 방지하기 위하여 피벗을 선택할 때 더욱 리스트를 균등하게 분할할 수 있는 데이터를 선택한다.
    (예를들어 리스트내의 몇개의데이터 중에서 크기순으로 중간 값을 피벗으로 선택한다.)

 

퀵정렬의 시간 복잡도

• 최선의 경우
  - 비교횟수
  

 

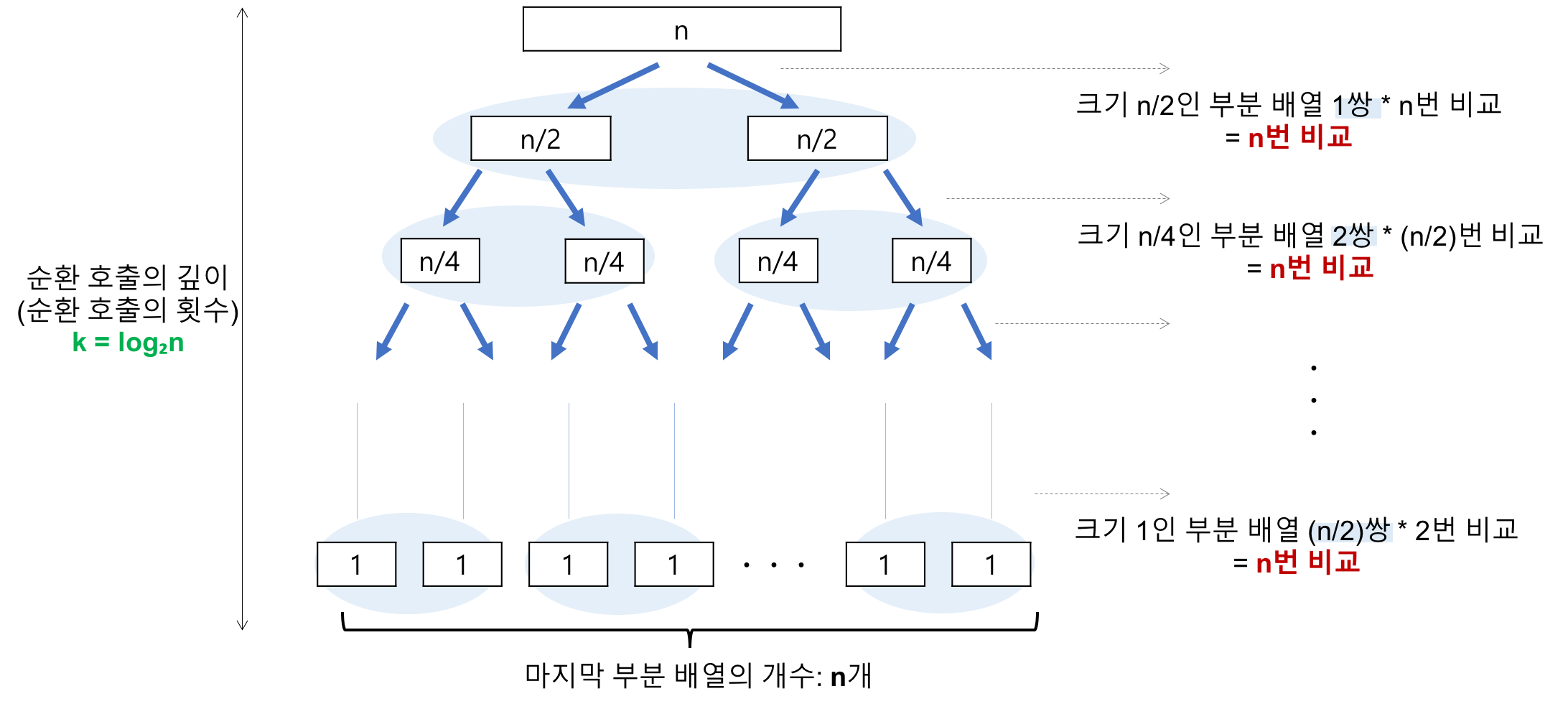
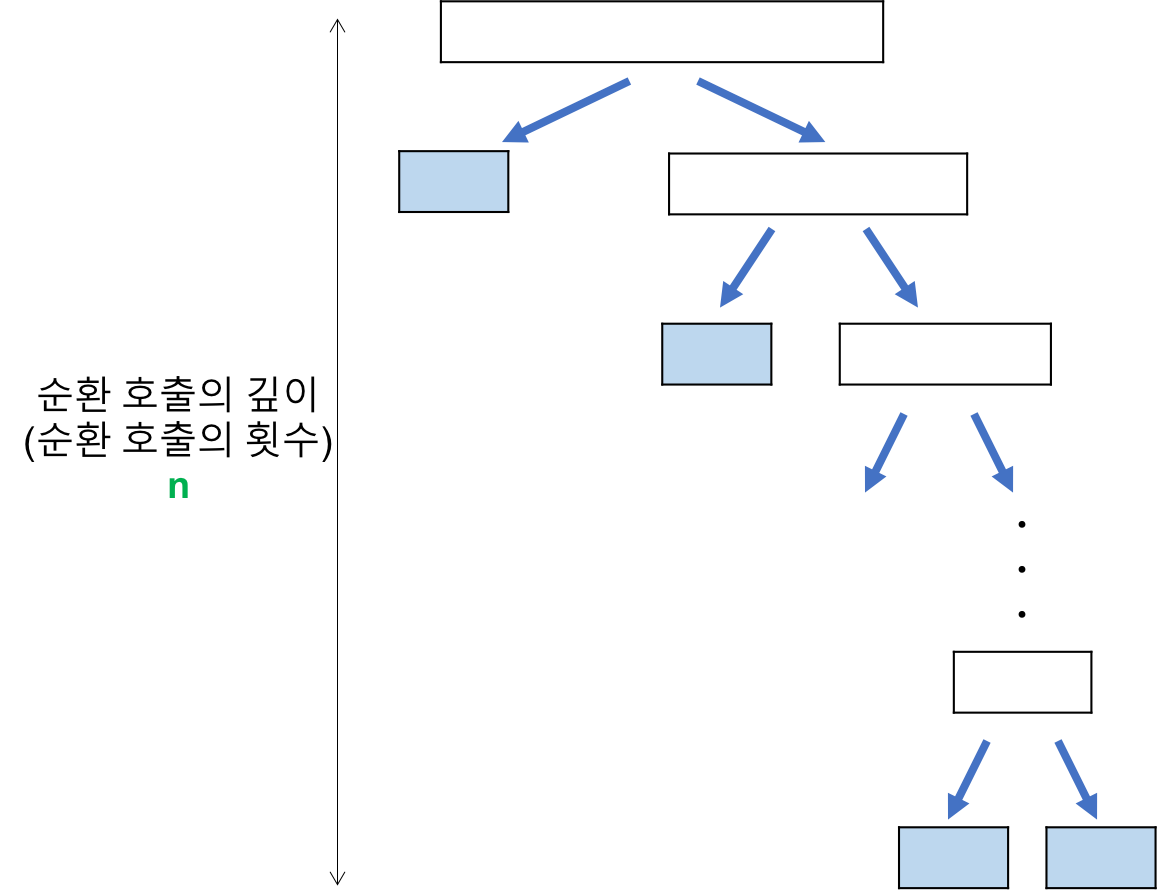
• 최악의 경우
  - 리스트가 계속 불균형하게 나누어지는 경우 ( 특히, 이미 정렬된 리스트에 대하여 퀵 정렬을 실행 하는 경우 )
  

 

퀵정렬 코드 (python)

 

기본 퀵정렬 코드

test_list = [3, 5, 65, 7, 45, 23, 33, 22, 11, 22, 11, 5]

def quick_sort(sort_list):
    if len(sort_list) < 2:
        return sort_list
    
    pivot = sort_list[len(sort_list) // 2]
    
    less_list, equal_list, greater_list = [], [] , []
    
    for i in sort_list:
        if i < pivot:
            less_list.append(i)
        elif i == pivot:
            equal_list.append(i)
        else:
            greater_list.append(i)
        
    return quick_sort(less_list) + equal_list + quick_sort(greater_list)
  
print(quick_sort(test_list))

퀵정렬의 결과는

		# 정렬 결과
        [3, 5, 5, 7, 11, 11, 22, 22, 23, 33, 45, 65]

 

위의 정렬 방식은 간단하면서도 재귀함수를 사용하는 방식의 문제풀이 방법이다, 하지만 입력이 커지면 커질수록 피벗값보다 작은 리스트, 같은 리스트, 큰 리스트들을 만들고 그 리스트들 안에서 또 작고 큰 리스트를 생성해야 하기 때문에 메모리의 비효율 성을 낳게 됩니다. 그러므로 메모리를 적게 사용하는 inplace 형식의 sort방법을 알아봅시다.

in-place형식의 퀵정렬 코드

test_list = [3, 5, 65, 7, 45, 23, 33, 22, 11, 22, 11, 5]


def quick_sort(sorting_list):
    left = 0
    right = len(sortin_list) - 1
    return sort(sorting_list, left, right)

def sort(sorting_list, left, right):
    if left >= right:
        return
    
    pivot = (left + right) // 2
    low, high = left, right
    
    while low <= high:
        while sorting_list[low] < sorting_list[pivot]:
            low += 1
        while sorting_list[high] > sorting_list[pivot]:
            high -= 1
        
        if low <= high:
            sorting_list[low], sorting_list[high] = sorting_list[high], sorting_list[low]
            low += 1
            high -= 1
            
    sort(sorting_list, left, high)
    sort(sorting_list, low, right)
    
    return sorting_list

print(quick_sort(test_list))

퀵정렬의 결과는

		# 정렬 결과
        [3, 5, 5, 7, 11, 11, 22, 22, 23, 33, 45, 65]
        

위의 값과 똑같이 나왔지만 이는 공간복잡도적인 측면에서 메모리를 덜쓴다는 점이 있다.