🚑 시작하기 앞서
필자는 Java를 주 언어로 사용하고 있기 때문에 모든 내용이 자바에 맞춰져있다. 이전에는 Python 내용도 다루고 했었지만, 현재는 Java만 공부하고 있기 때문에 타 언어에 대해서는 아쉽지만 기회가 된다면 재 포스트를 해보도록 하겠다.
🤔 비교 정렬? 비교 정렬이 아닌 정렬?
모든 정렬은 기본적으로 배열의 요소를 검사하는 과정을 거친다고 한다.
그래서, 흔히 아는 힙 정렬, 병합 정렬 등이 비교 정렬에 속한다.
비교 정렬이란?
요소간의 상대적인 크기를 이용해 정렬하는 알고리즘을 뜻함비교정렬 중 가장 빠른 속도를 가진 퀵 정렬, 병합 정렬, 힙 정렬이
O(N logN)의 시간 복잡도를 가진다.
비교 정렬은 데이터를 비교하기 위해 Decision Tree를 만들어 경우의 수를 따지는 데, 여기서 Decision Tree의 높이인 O(logN) 만큼 비교 연산이 이루어 진다는 것을 알 수 있다.
또한 비교 연산을 하기 위해 O(N)의 시간 복잡도를 가지는데,
이렇듯 비교 정렬은 아무리 빨라도 O(N logN) 보다 빠를 수 없는 것이다.
하지만, 비교를 하지 않고 정렬하는 방법인 Non-Comparison sort가 존재하는데,
여기에 오늘 포스팅 할 내용인 계수(counting) 정렬이 속해있다.
번외로 Radix sort(기수 정렬)도 이에 해당한다. 하지만 이번 챕터는 계수 정렬만 다루겠다.서론이 길었다. 다시 본론으로 넘어가자면,
계수 정렬은 아까 비교 정렬에서 봤던 Decision tree의 제약이 없기에 더 빠른 정렬이 가능하다고 한다.
얼마나 빠르냐면 O(N + 데이터의 최대값 K)의 시간 복잡도를 보장한다고 한다. 이전에 봤던 O(N logN)보다 빠르다.
그렇다면 이제 계수 정렬에 대해서 자세히 알아보도록 하자
😊 계수(카운팅) 정렬이란? 그리고 정렬 방법
계수 정렬은 말 그대로 배열에 데이터 값이 몇 번 등장했는지 카운트해주는 정렬이다.
계수 정렬이 어떻게 동작하는지 알아보도록 하자,
✨ 정렬 방법

- 먼저 위와 같은 배열이 존재한다고 가정하자,
- 배열의 크기는 총 11 (0~10) , 수의 범위는 (0 ~ 7) 까지 존재한다.
1) Phase 1: Array 배열의 각 값의 개수 구하기
array를 한 번 순회하여 각 값을 구할 때, 해당 값을 index로 하는 새로운 배열을 생성에 해당 index에 값을 1 증가시킨다.
해당 과정을 그림으로 먼저 보여주고 다시 설명해보겠다.
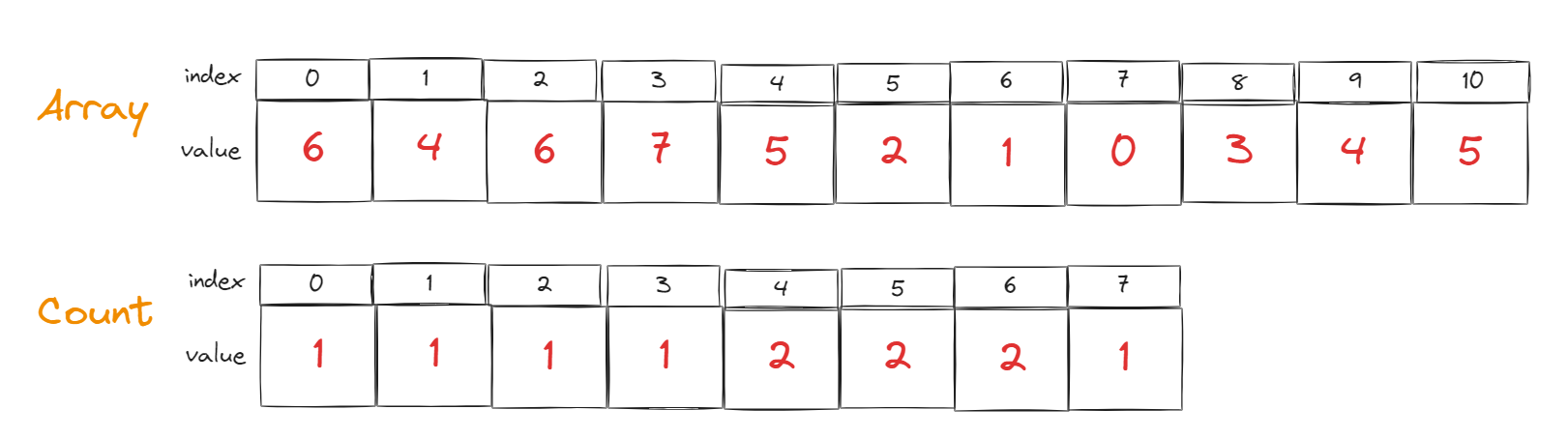
즉, Array index 0 번째 값인 6은 count 배열의 index 6번째에 값을 1 증가시킨다.
Array[0] = 6 / count[6]에 1증가,
Array[1] = 4 / count[4]에 1증가,
.....
Array[10] = 5 / count[5]에 1증가
이런식으로 총 Array의 길이만큼 반복해서 계산하면 Count 배열과 같이 나올 수 있다.
Count배열을 좀 더 살펴보자면
Count[0]은 즉, Array 배열에 값인 0을 의미
Count[0] = 1에서 1은 Array 배열에 값인 0이 1번 등장했다는 것을 의미말이 어려웠다. 좀 더 쉽게 정리하자면
Count index = Array 배열에 등장한 수(값)
Count value = Array 배열에 등장한 수의 등장 횟수
2) Phase 2: Count 배열의 각 값의 누적합 구하기
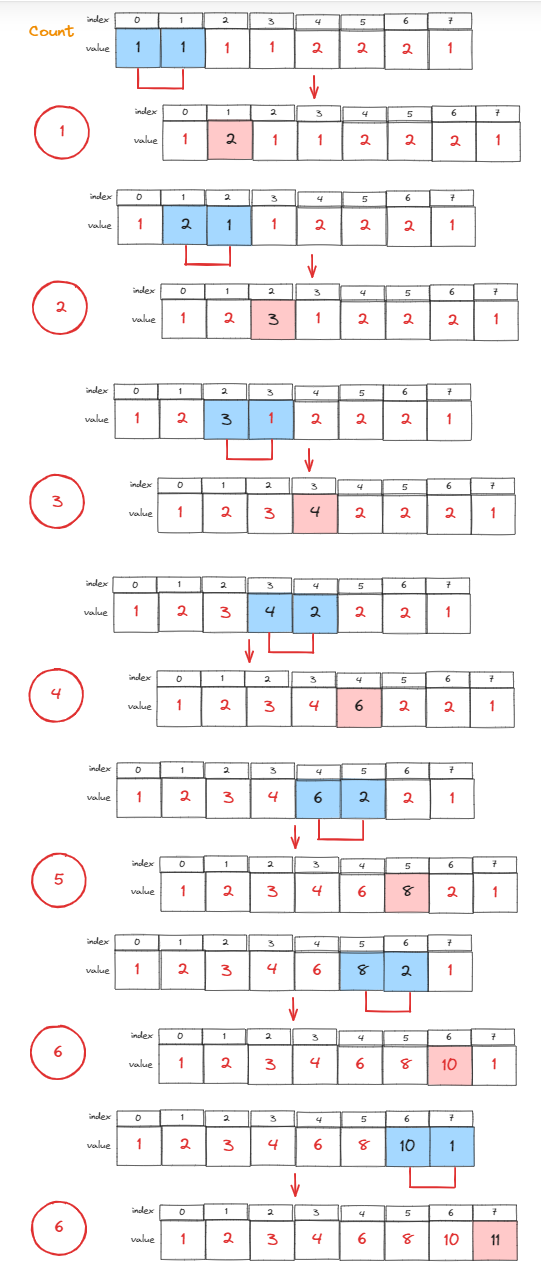
이런 형태로 count[1] ~ count[7]까지 누적합을 계산해준다.
그럼 아래와 같은 그림으로 배열이 만들어진다.
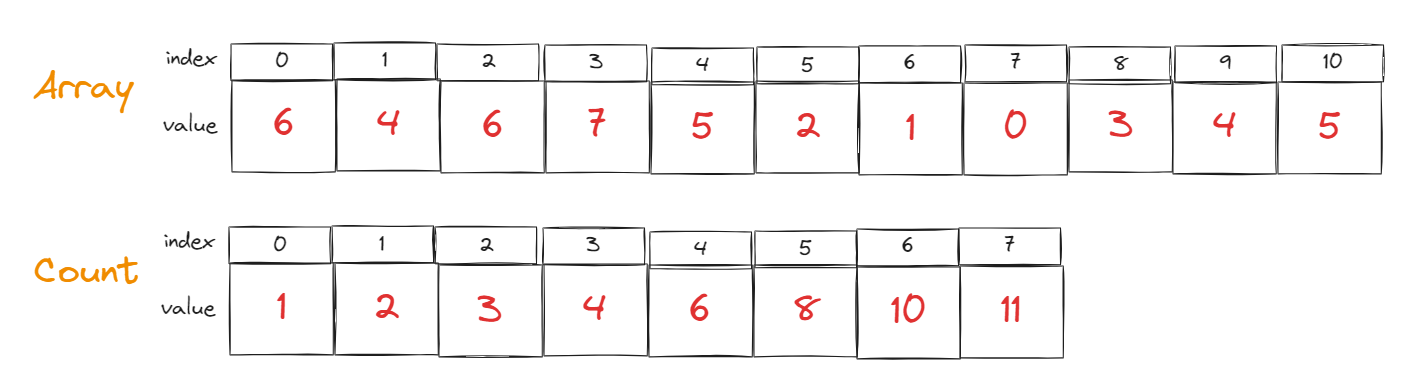
3) Phase 3: Count배열의 값은 정렬된 위치를 알려준다.
Count 배열의 각 값은 Array에 정렬된 값의 인덱스를 나타내주는데, 부연 설명을 더하자면
Count 배열의 각 값에서 -1을 해주면 이것이 정렬된 Array 배열에서 위치할 인덱스 값이 된다.
Array[0] = 6이고, Count[6] = 10인데, 여기서 10-1을 해주면 6은 곧 9번째 인덱스에 위치하는 것을 의미한다.
이를 그림으로 나타내면 좀 더 이해가 쉽다.
Phase 3은 마지막 인덱스부터 순회해서 진행해야 안정적으로 정렬이 가능하다는데, 그 이유는 중복되는 값이 존재할 수 있기 때문에, 뒤부터 진행하는 것이다.
얼렁뚱땅 넘겼지만, 뒤에서 진행하는 이유를 조금 더 명확히 파악하면 다시 업데이트 하겠다.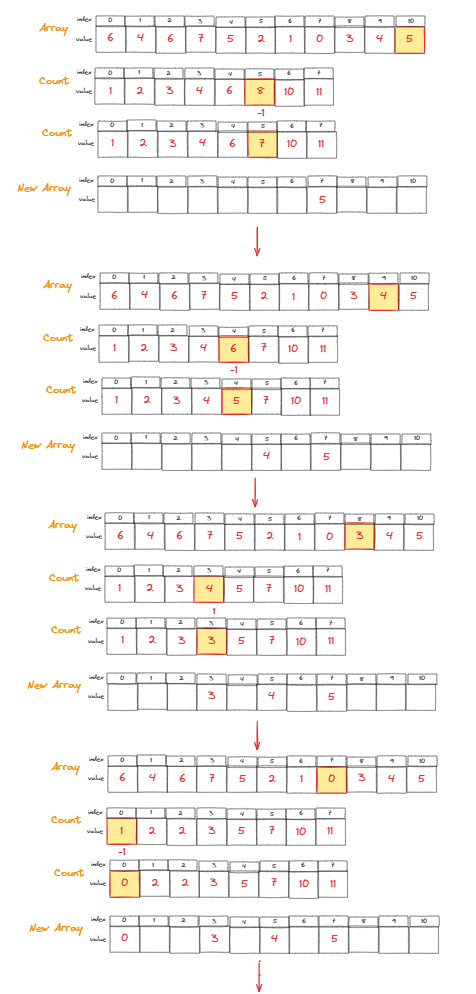
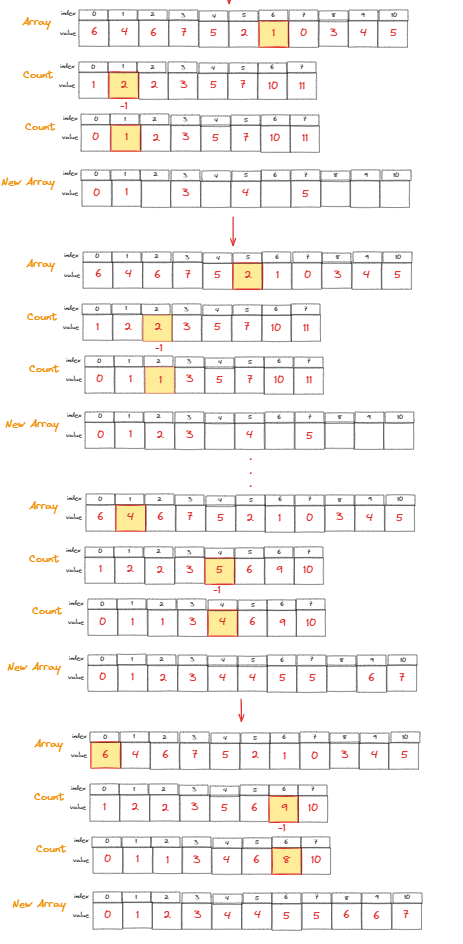
이런 형태로 구할 수 있는 것이다.
비하인드 스토리로.. 손수 노가다로 풀다가, 잘못 계산해서 1시간을 날려먹었다.계수 정렬은 위에서 얘기한대로 비교하는 과정이 없기 때문에 O(N + (데이터의 최대값)K)으로 빠르게 계산할 수 있다.
하지만, 단점 역시 존재하기 때문에! 비교 정렬이 존재하는 것
- Array 배열외 Count라는 배열을 새롭게 만들어 줘야 한다.
Count배열은 Array배열에 존재하는 수의 범위만큼 길이가 존재해야 하는데,
즉, 수가 0~ 10까지면 10개의 크기만큼 존재해야 한다. 근데 0 ~ 10억개면??
적은 원소의 수를 정렬하기 위해 많은 메모리를 낭비할 수 있는 문제가 발생한다.
즉, 정렬하고자 하는 원소의 개수보다는 원소의 수의 범위가 작다면
(0 ~ 10) > (0 ~ 1000) 효율적이겠지만, 그렇지 않다면
상황에 맞게 퀵 정렬 혹은 병합 정렬 등이 더 효율적일 수 있다.🤢 실제 코드(구현 코드)
public class CountingSort {
public static void main(String[] args) {
int[] arr = new int[50]; // 정렬하고자 하는 원소의 개수
int[] count = new int[101]; // 원소의 수의 범위 (0 ~ 100)
int[] new_arr = new int[50]; // 정렬 될 새로운 배열
for(int i = 0; i< arr.length; i++) {
arr[i] = (int)(Math.random() * count.length);
}
// Phase 1: Array 배열의 각 값의 개수 구하기
for(int i = 0; i<arr.length; i++) {
count[arr[i]]++;
}
// Phase 2: Count 배열의 각 값의 누적합 구하기
for(int i = 0; i < count.length-1; i++) {
count[i+1] += count[i];
}
// Phase 3: Count배열의 값은 정렬된 위치를 알려준다.
for(int i = arr.length-1; i >=0; i--) {
// 계속해서 --을 해줘야 하기 때문에 -1을 해주면, 해당 값이 영향(변하지) 받지 않음
// 즉 5-1 = 4 / 4 -1 =3을 해줘야 하는데, 게속 5-1 = 4 를 출력하게 됨 -1로 하면
count[arr[i]]--;
new_arr[count[arr[i]]] = arr[i];
}
// Phase 4: 출력해보기
for(int i = 0; i< new_arr.length; i++) {
if(i % 10 ==0) {
System.out.println();
}
System.out.print(new_arr[i] + " ");
}
}
}
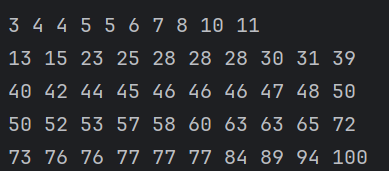
잘 정렬되서 나오는 것을 확인할 수 있다.🤢 회고
정렬에도 무수히 많은 방법 중 오늘 비교 정렬이 아닌 계수 정렬에 대해서 짧게나마 알아보았다.
아직 퀵정렬, 병합 정렬 등 알아야 정렬방법들이 산더미이지만, 하루에 하나씩 알아본다면 또 정렬을 마스터하는 날이 오지 않을까 기대한다.
