문제 url:
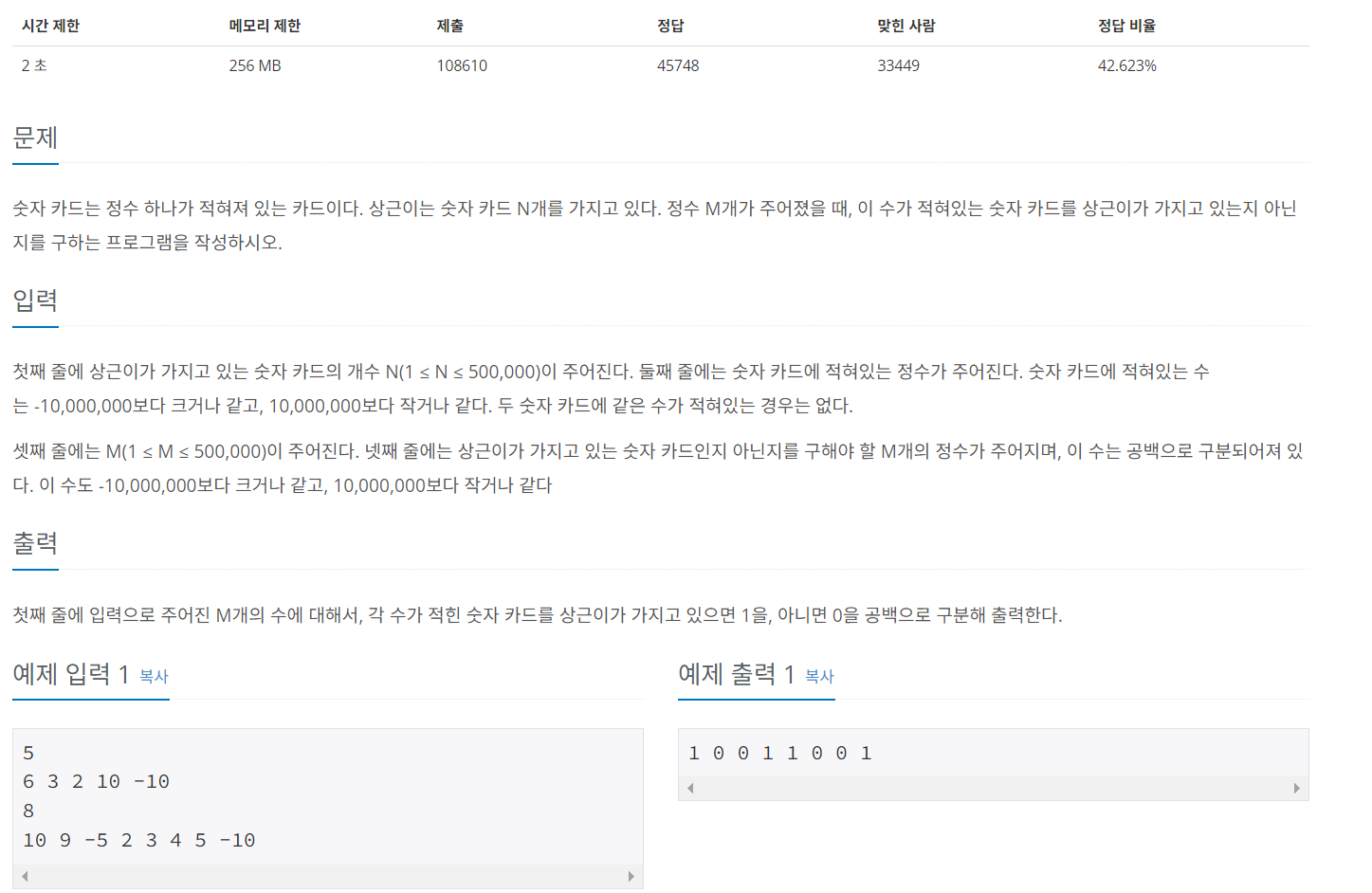
숫자 카드
문제:
🤔 문제 알아보기
저번에 좌표 압축 문제를 풀면서 HashMap에 대해서 써본 경험이 있다.
그때는 HashMap을 이용해 ranking 알고리즘을 풀어봤는데, 이번에도 유사하게 해당 방법을 사용해보고자 한다.
HashMap에 둘째 줄에 속한 값들을 넣어준 다음, 넷째 줄에 있는 원소값을 넣어, 값이 존재하면 1을 출력 그렇지 않으면 0을 출력하면 될 것 같다.
그럼 하나씩 문제를 살펴보자,
첫째 줄에 숫자 카드의 개수 N개를 입력받으며(1<= N <= 500,000)
둘쨰 줄에는 숫자 카드에 적힌 수를 입력받는다(-10,000,000 <= e1 <= 10,000,000)
셋째 줄에는 새로운 숫자 카드 M개 만큼 입력받고(1<= M <= 500,000)
넷째 줄에는 숫자 카드에 적힌 수와 비교하기 위한
숫자 카드를 입력 받는다. (-10,000,000 <= e2 <= 10,000,000)먼저, 수의 범위가 20,000,000 정도 된다. 계수 정렬을 해서 풀고자 하면, 조금 고민을 해봐야 겠다.
또한 N과 M이 각각 500,000개 까지 가능하기 때문에 O(N^2) 이상의 시간 복잡도가 구현되면 시간 초과가 나기 때문에 반드시 O(N) 또는 O(N logN)의 시간 복잡도로 풀어야 한다.
그럼 여기까지 문제를 살펴보고 코드로 넘어가보겠다.
🐱👤 실제 코드
import java.io.*;
import java.util.HashMap;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
HashMap<Integer, Integer> getCard = new HashMap<>();
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 1; i <= N; i++) {
getCard.put(Integer.parseInt(st.nextToken()), i);
}
int M = Integer.parseInt(br.readLine());
StringTokenizer st_choice = new StringTokenizer(br.readLine());
StringBuilder sbd = new StringBuilder();
for (int i = 0; i < M; i++) {
boolean getNum = getCard.get(Integer.parseInt(st_choice.nextToken())) != null;
if(getNum) {
sbd.append(1).append(" ");
} else {
sbd.append(0).append(" ");
}
}
System.out.println(sbd);
}
}
HashMap을 활용하니깐 그렇게 어려운 문제는 아니었다.
일단 코드를 하나씩 분리해서 본다면,
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 1; i <= N; i++) {
getCard.put(Integer.parseInt(st.nextToken()), i);
}이부분에서 왜 이렇게 짯을까? 궁금한 부분이라고 생각한다.
일단, 필자는 M개의 카드 숫자를 이용해 N개의 카드가 존재하는지를 파악하는 문제라고 생각했다.
그래서 카드 숫자를 key값으로 생각한 것이고 Value값에 대해서는 임의의 숫자인 i를 넣은 것이다.
해당 문제에서 필요한 건 결국 Key값에 대한 것이니
StringTokenizer st_choice = new StringTokenizer(br.readLine());
StringBuilder sbd = new StringBuilder();
for (int i = 0; i < M; i++) {
boolean getNum = getCard.get(Integer.parseInt(st_choice.nextToken())) != null;
if(getNum) {
sbd.append(1).append(" ");
} else {
sbd.append(0).append(" ");
}
}해당 로직이 이번 문제의 핵심 로직이다.
아까 설명했듯, Key를 이용해 해당 값의 존재여부를 확인한다고 했다.
그래서 HashMap.get을 이용해서 문제를 풀이하는데,
get()메서드는 O(1)의 시간 복잡도를 가지고 있어 굉장히 빠르다. 또한 get()메서드를 이용해서 값이 존재하지 않으면 null을 반환하는데,
이것을 활용하면 우리가 원하는 출력을 할 수 있다.

조금 더 찾아보니깐, Map 자료구조에서 get, put, remove, containsKey 등의 메서드는 O(1)의 상수 시간 복잡도를 가진다고 한다.
그러나, get()메서드도 충돌로 인해 모든 요소가 하나의 인덱스를 가지게 되면 O(N)의 시간 복자도를 가질 수 있다고 한다.
해당 내용은 조금 더 찾아서 따로 세션에 포스팅 해보도록 하겠다.
💢 트러블 슈팅
HashMap에 대해서 먼저 포스팅을 하고 해당 문제를 풀어볼 껄 그랬다.
그 이유는 처음에 ContainsValue()를 이용해서 풀었더니 시간 초과가 나온 것이다.
그러면 일단 로직은 맞다는 것이니.. ContainsValue()는 시간 복잡도가 느리다고 생각해,
이전에 잠깐 언급된 것을 봤던 O(1)의 방식인 get을 이용해 문제를 풀었던 것이다.
아래는 시간 초과가 된 코드이다.
import java.io.*;
import java.util.HashMap;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
HashMap<Integer, Integer> getCard = new HashMap<>();
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
getCard.put(i, Integer.parseInt(st.nextToken()));
}
int M = Integer.parseInt(br.readLine());
StringTokenizer st_choice = new StringTokenizer(br.readLine());
StringBuilder sbd = new StringBuilder();
for (int i = 0; i < M; i++) {
if(getCard.containsValue(Integer.parseInt(st_choice.nextToken()))) {
sbd.append(1).append(" ");
} else {
sbd.append(0).append(" ");
}
}
System.out.println(sbd);
}
}
containsValue()를 사용한 것을 찾아 볼 수 있는데, 그렇다면 왜 이게 시간 복잡도가 느린건지, 로우 코드에서 알아보도록 하겠다.
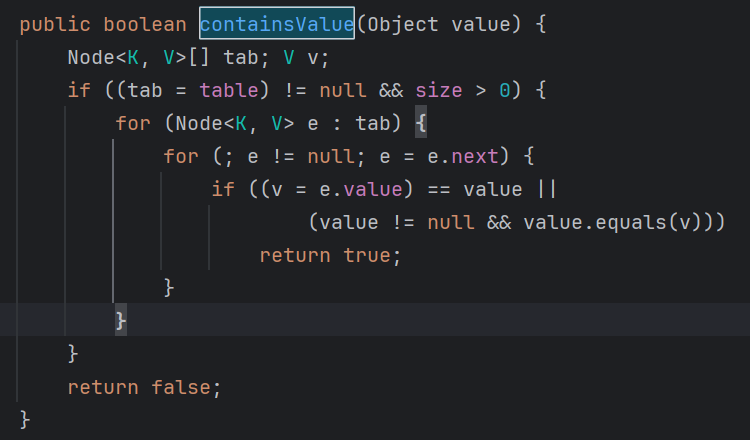
ContainsValue()메서드는 맵에 있는 모든 요소값을 확인해야 하기 때문에 O(N)의 시간 복잡도를 가진다고 한다.
for (int i = 0; i < M; i++) {
if(getCard.containsValue(Integer.parseInt(st_choice.nextToken()))) {
sbd.append(1).append(" ");
} else {
sbd.append(0).append(" ");
}
}그렇게 되면 해당 로직은 최악의 경우 O(N ^ 2)의 시간 복잡도를 가지게 되기 때문에 시간 초과가 발생하는 것이다.
🤢 코드 리팩토링
우리 블로그의 자랑은 바로 다양한 문제 풀이법 연습이다.
이번에도 역시 타 블로그를 탐방하면서 여러 풀이법을 봐왔다.
그 중에서 이번 문제는 이분탐색으로 풀 수 있다는 것을 보고 공부를 해보았다.
그럼 공부한 내용을 잠깐 얘기하면,
해당 문제를 for문으로 완전탐색을 수행한다면 O(N * M)의 시간 복잡도를 가진다.
즉, 500,000 * 500,000개의 연산 횟수가 생긴다는 의미다.하지만 이분 탐색을 한다면, O(M logN)의 시간 복잡도를 가질 수 있다고 한다.
500,000 log500,000 = 500,000 * 18.931xxxx 대락 1천만번의 연산 횟수를 가진다고 보면 된다.
필자가 배운 공식, 1초면 1억번 연산이 가능하다. -> 그렇다면 1천만번이면 혜자네?
바로 이진 탐색을 공부해보자!
먼저 첫 번째 TC를 가정해서 보자
6, 3, 2, 10, -10 이렇게 5가지가 존재한다. 이를 정렬하면
-10, 2, 3, 6, 10 으로 나타낼 수 있다.
해당 값에서 만약 내가 찾고싶은 값을 value라고 지칭하고 다음으로 넘어가서
이진 탐색은 left, mid ,right 총 3가지의 인덱스 값을 가진다.
여기서 mid는 중앙값을 의미하는데,
1. mid > value 라면 -> 중앙값보다 작기 때문에 left를 움직이며 탐색을 할 수 있다.
2. mid < value 라면 -> 중앙값보다 크기 때문에 right를 움직이며 탐색을 할 수 있다.
3. mid == value 라면 -> 같이 같기 때문에 종료
코드와 같이 해당 부분을 보면 이해가 쉬울 것이다.
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
static int N;
static int[]N_num;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sbd = new StringBuilder();
N = Integer.parseInt(br.readLine());
N_num = new int[N];
// N_num 배열에 공백으로 나눈 입력값 주입
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
N_num[i] = Integer.parseInt(st.nextToken());
}
// 이진 탐색을 위한 정렬
// 여기서 O(N logN)의 시간복잡도 사용
Arrays.sort(N_num);
int M = Integer.parseInt(br.readLine());
StringTokenizer st_m = new StringTokenizer(br.readLine());
for (int i = 0; i < M; i++) {
if(binarySearch(Integer.parseInt(st_m.nextToken()))) {
sbd.append(1).append(" ");
} else {
sbd.append(0).append(" ");
}
}
System.out.println(sbd);
}
static boolean binarySearch(int m) {
// 제일 왼쪽 인덱스 값이므로 0
int left_index = 0;
// 제일 오른쪽 인덱스 값이므로 length -1
int right_index = N-1;
while(left_index <= right_index) {
int mid_index = (left_index + right_index) / 2;
int mid = N_num[mid_index];
if (mid < m) {
left_index = mid_index+1; //mid값보다 크기 때문에 left를 땡겨와서 비교
} else if( mid > m) {
right_index = mid_index-1; //mid값보다 작기 때문에 rigth를 땡겨와서 비교
} else {
return true; // 값이 일치하면 true 반환
}
}
// while문을 돌았는데도 true를 반환하지 못했기 때문에
// 해당 로직까지 진입
// 즉 일치한 값이 존재하지 않는다.
return false;
}
}
binarySearch 메서드 파트를 잠시 확인하자면,
해당 그림을 보면 이해가 될 것이다.
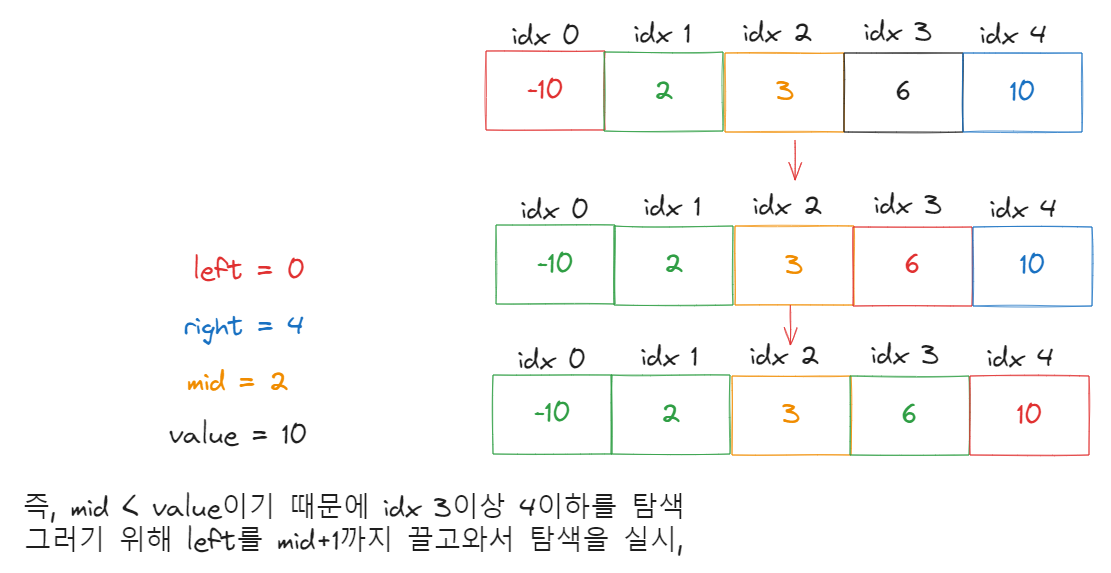
더 이해못하겠는데?
자 그림을 무선 살펴보면,
left = 0
right = 4 (5-1 = 4)
mid = 2 (0 + 4 ) / 2 = 2.5니깐 몫이 2
value를 10이라고 가정하자,
우리는, mid값을 이용해서 해당 값이 value와 같을 때까지 찾는데,
left가 right보다 커지거나, right가 left보다 작아질 때까지 찾을 것이다.
현재 풀이를 좀 더 해본다면,
mid < value이기 때문에
left = mid + 1을 해줘 현재 left값은 3이다.
그렇다면 다음 반복문에서 mid값은 (3 + 4 ) /2 = 3이다.
즉, 3번째 인덱스 6의 값을 가지게 되는데, 이를 value와 비교했을 때,
value가 더 크기 때문에 다시 left는 3+1로 4의 값을 가진다.
그럼 다음 반복문에서 mid값은 (4 + 4) / 2 = 4로
즉, 4번째 인덱스 10의 값을 가지며 mid와 value가 같아져 true를 반환한다.
만약 해당 값이 없다면, left는 4+1 = 5를 가지며 right보다 커져 반복문이 종료되며 false를 반환할 것이다.
그렇다면, mid > value라면, 해당 로직의 반대라고 생각하면 될 것이다.
이상으로 짤막한 이분탐색을 얼렁뚱땅 설명해보았다..
필자가 아직 초보라 말을 잘 못한다 계속해서 고쳐나가겠다

해시맵 방식 -> 956ms
이분탐색 방식 -> 1316ms
이분탐색이 메모리는 적게들지만, 속도는 O(M log N)으로 시간이 더 걸렸다.
😎 계수정렬
해당 포스팅을 적고 마무리 짓던중, 계수정렬도 가능하지 않을까? 메모리 낭비가 있어도?
이때 나를 말렸어야 했다.. 급하게 다시 노트북을 켜서 계수정렬로 풀어보았다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sbd = new StringBuilder();
int N = Integer.parseInt(br.readLine());
int[]N_arr = new int[20000001];
StringTokenizer st_n = new StringTokenizer(br.readLine());
for (int i = 0; i < N; i++) {
N_arr[Integer.parseInt(st_n.nextToken()) + 10000000]++;
}
int M = Integer.parseInt(br.readLine());
StringTokenizer st_M = new StringTokenizer(br.readLine());
for(int i = 0; i < M; i++) {
if(N_arr[Integer.parseInt(st_M.nextToken()) + 10000000] > 0) {
sbd.append(1).append(" ");
} else {
sbd.append(0).append(" ");
}
}
System.out.println(sbd);
}
}
메모리 차이는 좀 있지만, 더 성능이 좋아져서. 아 메모리가 좀 낭비되더라고 시도는 해보자 라는 경험을 해볼 수 있었던 번뇌였다.
계수정렬에 대해서는 이전에 풀었던 정렬 문제를 한번 확인해주면 감사하겠다.
귀찮은 분을 위해 간략히 로직을 말씀드리자면,
수는 -10,000,000 <= e <= 10,000,000의 범위를 가지기 때문에,
배열의 크기는 총 20,000,001을 잡았다. (1은 0의 인덱스값을 위해)
그런 다음 해당 인덱스의 값에 1씩 증가하여, 해당 값의 존재유무를 파악한다.
문제 조건에서 값이 중복해서 들어오지 않는다는 것을 본 후,
이런 로직도 가능하다는 것을 생각해보았다.그런 다음, M개만큼 숫자를 받아 해당 인덱스에 0보다 크면(숫자가 존재) 1을 출력 그렇지 않으면 0을 출력하여 문제를 풀 수 있는 것이다.