[Java] 백준 11653번: 소인수분해

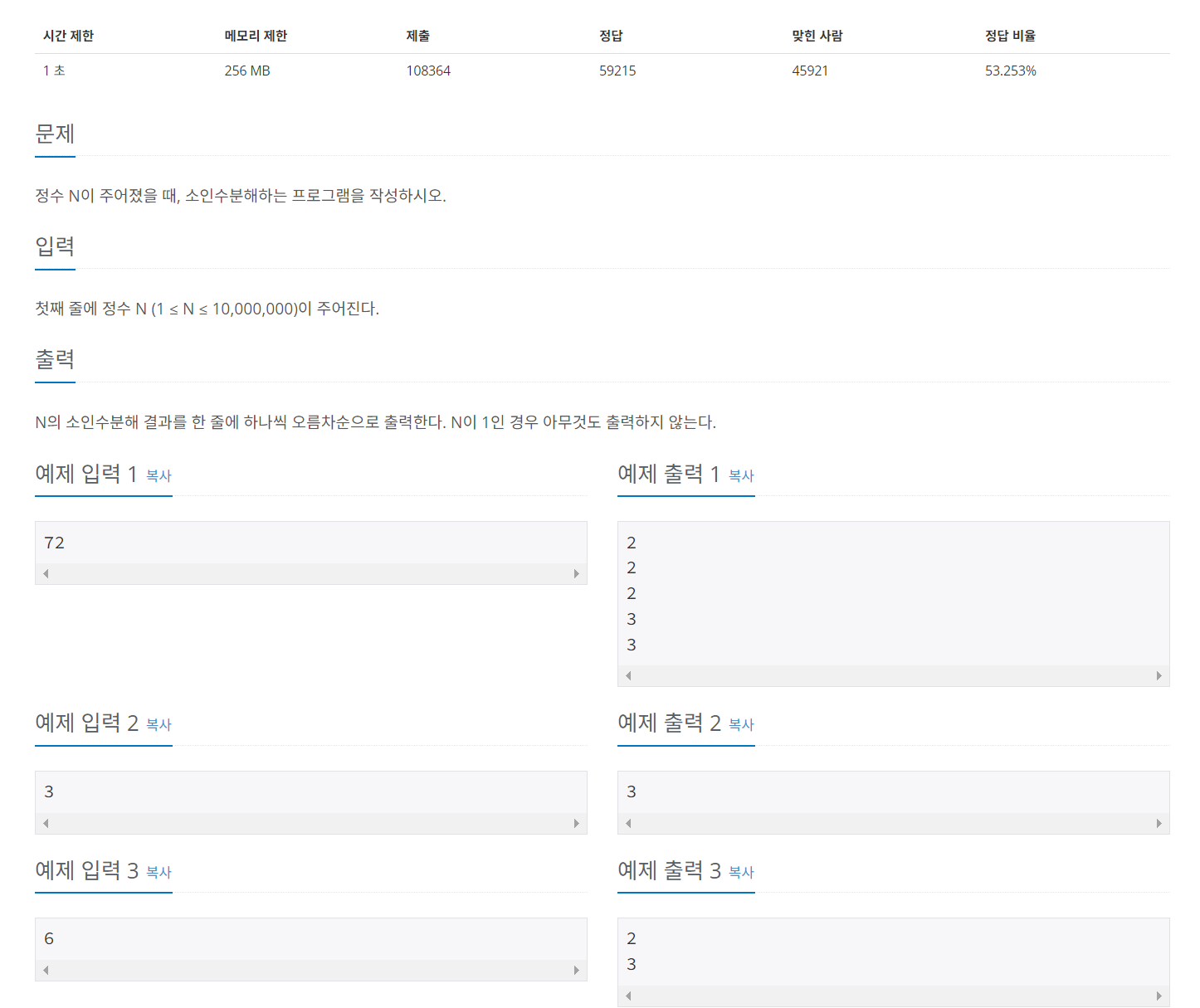
문제 url:
소인수분해

문제:

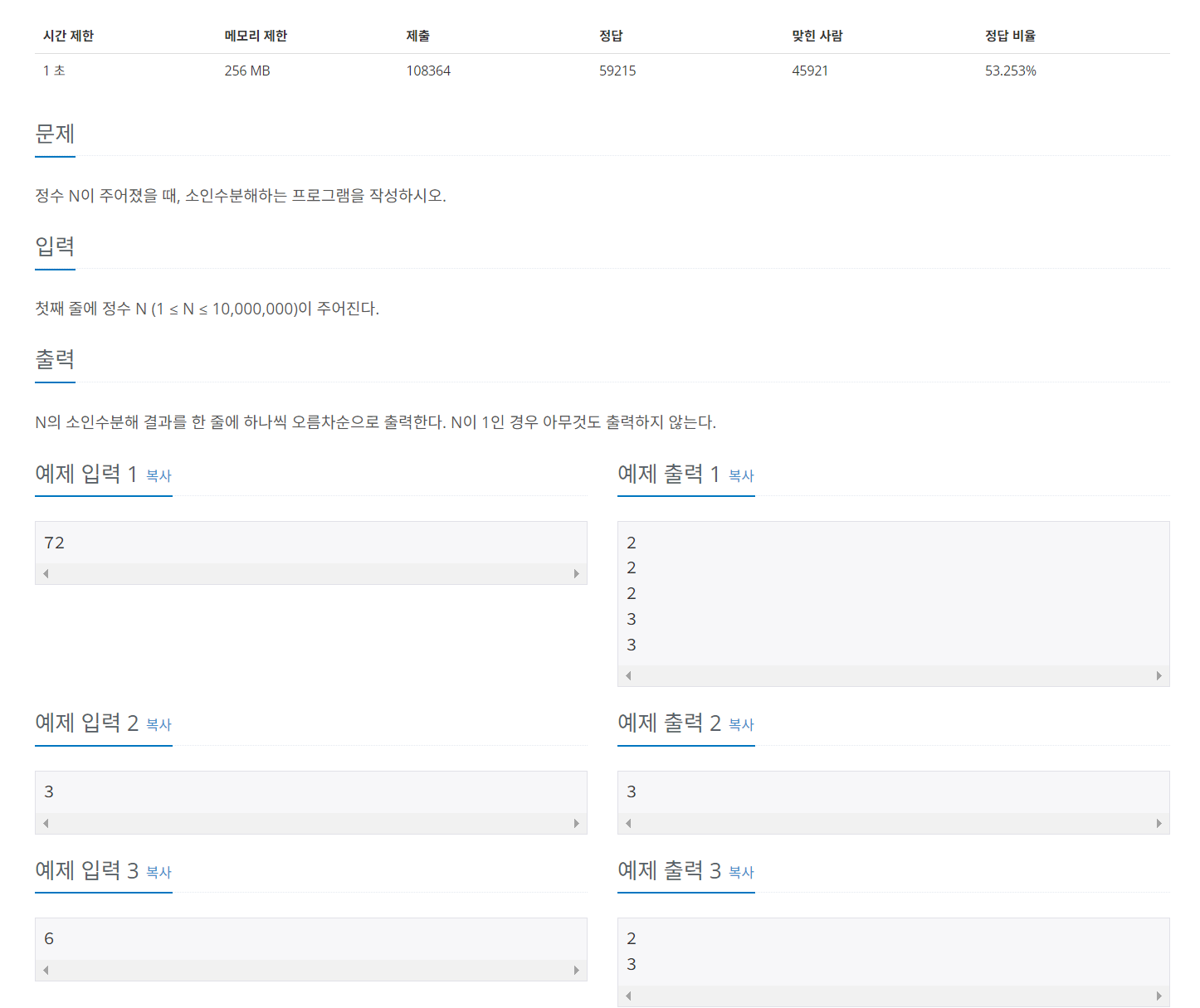
🤔 문제 알아보기

문제를 알아보기 이전에 소인수분해에 대해서 알아보자.

소인수분해란?
1보다 큰 자연수를 소인수(소수의 인수)들만의 곱으로 나타내는 것 또는 합성수를 소수의 곱으로 나타내는 법.

소인수분해를 영어로 하면 prime factorization 라고한다. prime이 소수를 의미하는데, 간단하게 설명하면 소수의 곱으로 나타낸 값이라고 보면 될 것 같다.

소인수분해에 대해 개념을 알아봤으니 이를 코드화 시켜보자

• 대충 10이하의 소수에는 2,3,5,7이 존재한다. 그렇다면 초기값을 2로 지정한다.

• N을 초기값 2로 나누어 떨어질 때까지 반복한 후 N을 나눈 몫으로 초기화

  • 

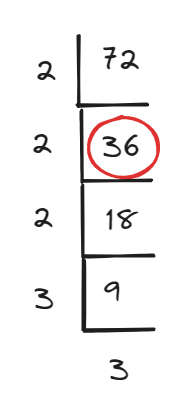
  • 위의 사진을 봤을때, 72를 나눈 후 36에 대해 소수를 나누어야 한다는 얘기이다.

• 소수가 현재 N을 나누었을 때 나머지가 존재한다면, 다음 소수로 나눌 수 있도록 한다.

• 그 후 문제의 규칙에 맞게, 소수를 들여쓰기와 함께 출력, N = 1일경우는 출력하지 않는다.

😎 준비하기

1. BufferedReader를 통해 입력을 받는다.
2. N을 입력받은 후, 소수로 나눌 변수(prime)를 2로 초기화 해주며 정의
3. 본문의 규칙에 따라 N이 1일 경우 출력하지 않도록 한다.
4. N이 prime과 나누었을 때, 나머지가 0이 아닐때까지 나누고 나눈 몫을 
다시 N에 초기화 후 prime 출력
5. 그런 다음 나눌 수 없을 때, prime++를 통해 값을 변경

🐱‍👤 실제 코드

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());
        int prime_num = 2;

        if (N == 1) {
            return;
        }

        while(true) {

            while(N % prime_num == 0) {
                N /= prime_num;
                System.out.println(prime_num);

            }

            if ( N != 1) {
                prime_num++;
            } else {
                break;
            }
        }
    }
}

😁 코드 해석

특별히 어려운 코드는 아니지만, 다른 이를 위해 왜 이렇게 구성했는지 설명하자면,

while(N % prime_num == 0) {
     	N /= prime_num;
       	System.out.println(prime_num);

}

참일 때 계속 N을 prime_num(초기값 2인)으로 나눈 다음 몫을 N에 초기화 시켜 계속 N의 값을 쪼개어 줄여나가며 본문에서 인수를 계속 출력하라고 했기에 출력.

if ( N != 1) {
     prime_num++;
   } else {
      break;
   }

N이 1이 아니라는 것은 즉, 마지막까지 나눠지지 않았다는 의미로 즉 더 나누어 질 수 있는 상태를 의미한다.
그렇지만, 현재 prime_num값으로는 N을 딱 나누어 떨어질 수 없는 값이기에 prime_num++을 하게 되는 것이다.

만약 N = 1이라면, 현재 소인수분해가 완료됐음을 의미하기에 제일 상위의 while문을 빠져나가도록 break문을 사용

😢 코드 리팩토링

알고리즘 문제를 푸면서 요즘 부쩍 신경쓰는 것이 있다면,
얼마나 더 빠르게 메모리는 더 적게, 코드 길이는 짧게 코드를 짤 수 있을까? 이다.
필자는 아직 연습이 덜 된 상태라서 하드코딩을 해도 문제는 맞춰보자는 부분에 초점을 두다보니 아쉬운 부분이 많다.

그래서 이번에도 역시 다른 블로그와 타 코드를 비교해보며 코드 리팩토링을 진행해보겠다.

현재 문제는 불필요한 while문이 존재, while문이 2번씩이나 사용된다는 점과 이로인해 난잡함과 코드가 길다는 점이 존재한다.

그래서 이를 줄일 수 있도록 해보았다.

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());

        if (N == 1) {
            return;
        }

        for (int i = 2; i <= Math.sqrt(N); i++) {
            while (N % i == 0) {
                System.out.println(i);
                N /= i;
            }
        }

        if (N != 1) {
            System.out.println(N);
        }
    }
}

먼저 알아볼 for문에 대해서 분석을 해보자

---

for (int i = 2; i <= Math.sqrt(N); i++) {
            while (N % i == 0) {
                System.out.println(i);
                N /= i;
            }
        }

우리가 소수를 구할 때 2<= p <= sqrt(N)인 범위에 있는 모든 소수 p로 n을 나누어 보아, 나누어 안 떨어지면 소수임을 배울 수 있었는데, 이번에는 조금 간단하게 설명하자면,

합성수(서로 다른 두 개 이상의 소수의 곱으로 이루어진 수.)는 A X B = C(합성수)로 이루어진다.

즉 (1 <= A, B < C) 해당 공식이 성립할 수 있는데,
만약 A와 B가 제곱근 C보다 값이 크다면 논리가 안맞을 수 있다.
즉, A, B > √C가 된다면 A X B = C가 아닌 A X B > C가 되기 때문에
A, B는 적어도 한개는 √C보다 작거나 같아야 한다고 보면 된다.

그래서 N의 제곱근까지 반복을 하는 것이다.

if문 코드에 대한 코드리뷰는 다음과 같다

---

if (N != 1) {
    System.out.println(N);
   }

만약 11과 같이 나눌 수 있는 소수가 존재하지 않는다면, 출력될 수 없을 것이다.
반복문을 돌아도. 조건에 부합한 값이 없기 때문에

그렇다면 해당 코드는 출력을 하면 안되는 것인가?
그렇지 않다. 11 역시 소인수분해를 하면 11 그대로 나와야 하기 때문에 이 역시 출력할 수 있도록 조치를 취해야 하는데, 이것이 해당 코드이다.

이런식으로 코드 리팩토링을 진행해보았으며, 진행한 결과

시간도, 메모리도 줄어든 것을 볼 수 있다.

🤢 회고

조금 빨리 푼다고, 좀 어렵게 생각을 해서 풀었다. 근데 아뿔싸 시간초과라는 문구가 뜬 것이다. 이전에 배웠던 지식을 총동원해서 풀었는데, 이것이 시간초과를 가져오게 된 것이다.

이런 것을 느끼면서 문제를 풀 때는 좀 유연하고 간단하게 생각하는 것도 중요하다는 것을 깨우칠 수 있었고, 코드의 유연성에 많은 연습을 해야겠다는 생각을 가질 수 있었다.

아래는 시간초과가 뜬 코드이다.

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());
        int isPrime = 2;

        if (N == 1) {
            return;
        }

        while(true) {

            if (N == isPrime) {
                System.out.println(isPrime);
                break;
            }

            if(N % isPrime == 0) {
                N = N / isPrime;
                System.out.println(isPrime);

            } else {
                isPrime++;

                while(!getPrimeNumber(isPrime)) {
                    isPrime++;

                }

            }

        }

    }

    public static boolean getPrimeNumber(int num) {
        for(int i = 2; i <= Math.sqrt(num); i++) {
            if(num % i == 0) {
                return false;
            }
        }
        return true;


    }

}

소인수분해를 할 때 해당 값이 소수인지 아닌지 판별하는 메서드를 생성하였고 이를 통해 검증하게 하였는데, 알고보니 해당 작업을 위에도 이미 하고 있기 때문에 필요없는 코드였던 것이다. 또한 이전 코드에 비해 더 복잡하게 되면서 시간 초과가 왜 생겼는지 분석할 겨를도 없었다.
그 후 나중에 getPrimeNumber 메서드는 이미 위에서 중복적으로 시행중이었단 걸 알게된 후, 삭제 하였다.