[Java] 백준 13241번: 최소 공배수

문제 url:
최소 공배수

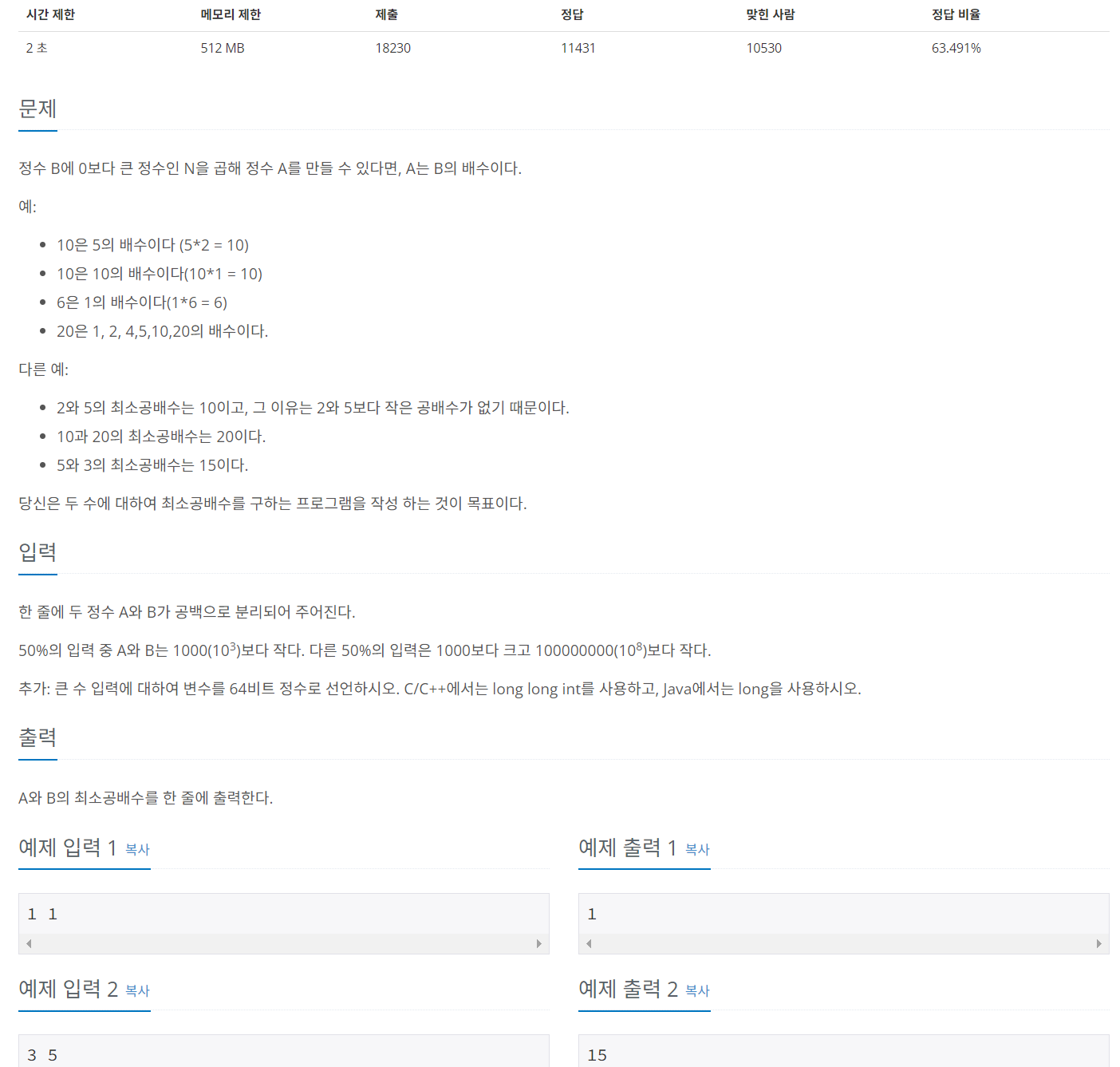
문제:

🤔 문제 알아보기

---

자 문제는 제목에서도 나와있듯, 최소 공배수를 구하는 문제이다.

최소 공배수란?
두 수, 혹은 그 이상의 수들의 공통인 배수를 공배수라고 한다. 즉, 최소 공배수는 해당 공배수가 가장 작은 값을 의미한다.

여기까지 문제를 알아보았고, 조건을 같이 알아보자
50%의 입력은 1000보다 작은데, 나머지는 1000< A,B < 100,000,000(1억) 보다 작다.
그래서 해당 입력 타입을 int가 아닌 long을 활용하라고 한다. (Java 기준)

이번 문제는 유클리드 호제법을 사용해서 풀어보겠다.
유클리드 호제법은 옆의 링크를 통해 알아볼 수 있다. -> 유클리드 호제법이란?

유클리드 호제법의 시간 복잡도는 O(log N)의 값을 가지는데, 여기서 N은 A와 B 중 가장 작은 값을 가진다. -> O(log min(A,B))라고 볼 수 있다.

또한 만약 하나씩 대입해서 찾는다고 가정하면, 시간복잡도는 O(N)의 값을 가진다.
그 외로 같은 시간복잡도를 가지는 문제에는 이진탐색( O(log N))이 있을 수 있다.

브루트 포스 방식 by chatgpt

public class GCD {
    public static int gcdBruteForce(int a, int b) {
        int gcd = 1;
        for (int i = Math.min(a, b); i >= 1; i--) {
            if (a % i == 0 && b % i == 0) {
                gcd = i;
                break;
            }
        }
        return gcd;
    }

    public static void main(String[] args) {
        int a = 48;
        int b = 18;
        System.out.println("GCD: " + gcdBruteForce(a, b));
    }
}

이진 탐색 방식

 static long gcdBinarySearch(long A, long B) {
        long lo = 1;
        long hi = Math.min(A,B);
        long gcd = 1;

        while (lo <= hi) {
            long mid = (lo + hi) / 2;

            if(A % mid == 0 && B % mid == 0) {
                gcd = mid;
                lo = mid + 1;

            } else {
               hi = mid -1;
            }
        }

        return gcd;
    }

근데, 두 방식으로 풀면 오답이 나온다.

🐱‍👤 실제 코드

---

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        long A = Integer.parseInt(st.nextToken());
        long B = Integer.parseInt(st.nextToken());

        System.out.println(A * B / gcd(A,B));


    }

    static long gcd(long A, long B) {
        while(B != 0) {
            long r = A % B;
            A = B;
            B = r;
        }

        return A;
    }
}

코드 풀이는 따로 하지 않겠다. 유클리드 호제법을 보고 왔다면 바로 알 수 있기 때문이다.
그래도 귀찮은 분을 위해 설명하자면,

유클리드 호제법은 gcd(a,b) = gcd(b,r)으로 a,b의 최대공약수는 b,r의 최대공약수와 같다. 여기서 r은 a % b를 한 값 이다.
즉, 이를 r이 0이 될 떄까지 반복하고 나온 b의 값이 곧 a,b의 최대공약수의 값이다.

A = 15, B = 6일때 gcd(15, 6) = gcd(6, 4) -> gcd(6,4) = gcd(4,2) -> gcd(2, 0) 그래서 해당 A와 B의 최대공약수는 2로 구할 수 있다.