[Java] 백준 13909번: 창문 닫기

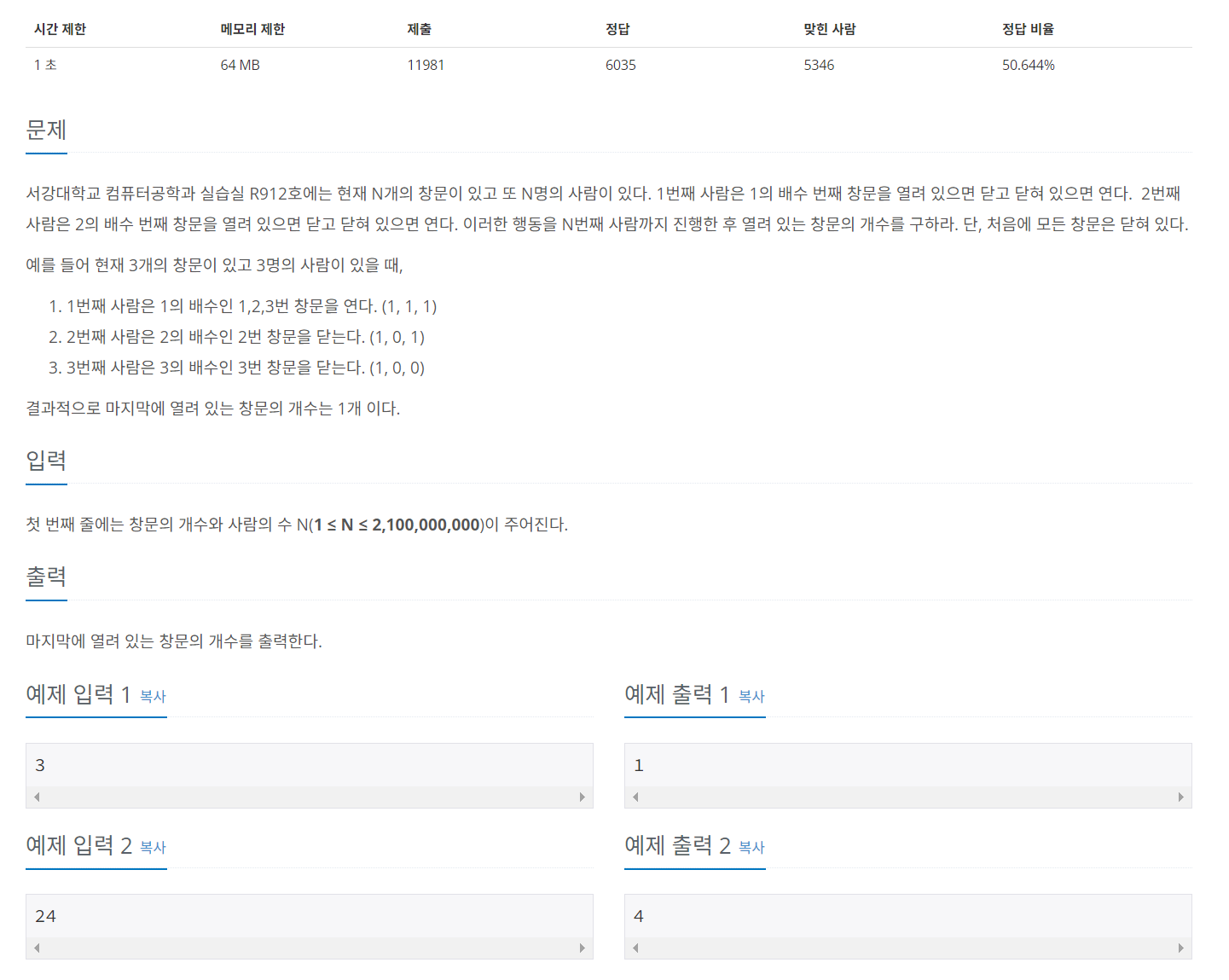
문제 url:
창문 닫기

문제:

🤔 문제 알아보기

---

흠...일단 처음에 봤을 때는 무슨말인지 이해를 못했다.. 그래서
손수 노트에 필기를 하며 해보았다.

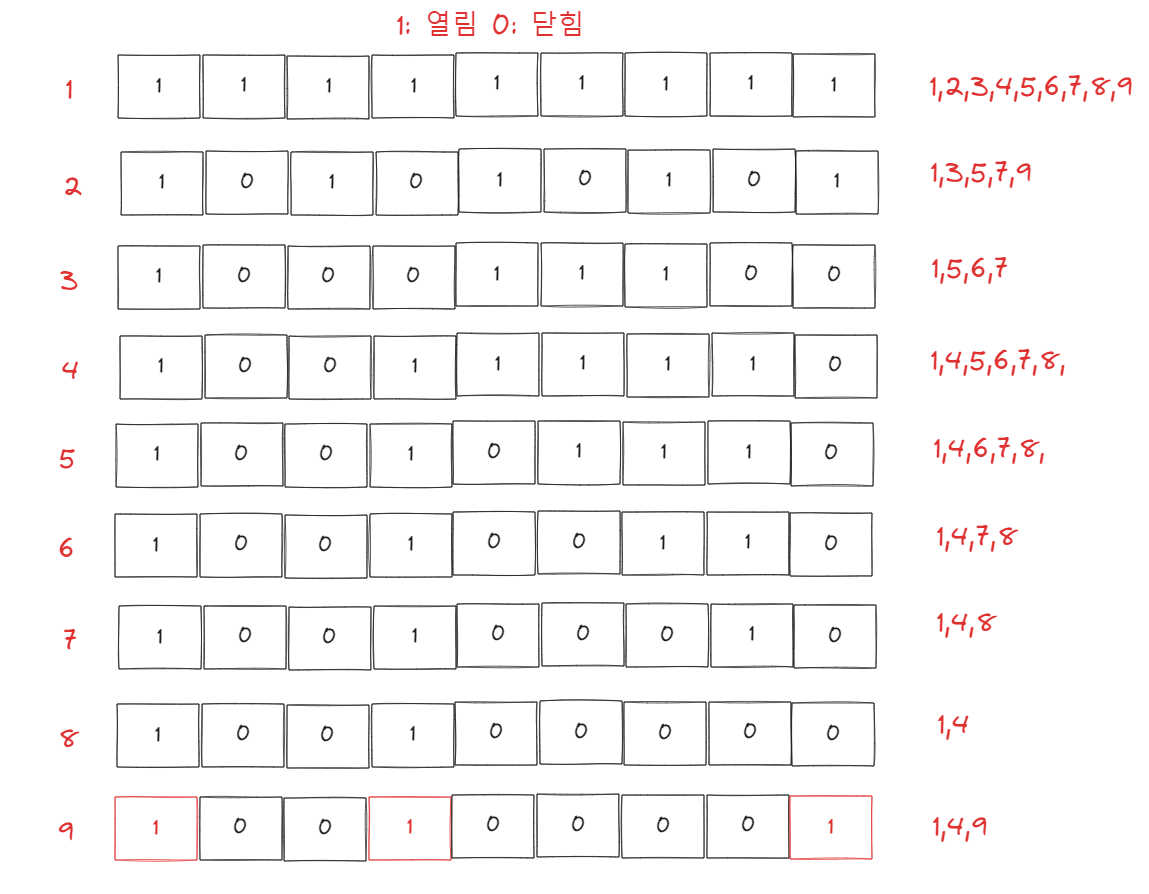
필자는 i가 9일 때를 생각해서 작성해봤다. 그런 후 마지막 9가 됐을 때,
무언가 익숙한 숫자가 보이는데 1, 4, 9 이건 분명 제곱수의 모습이다.

이때 필자는 해당 문제는 제곱수의 개수를 묻는 것이라고 생각을 했으며,
즉, n의 제곱근을 구한다면 해당 문제를 맞출 수 있다.

필자는 노트필기를 하면서 규칙성을 발견하여 또 다른 의견을 보고자 타 블로그를 참고해봤는데,

여기서는 약수의 개수가 (열고, 닫고, 열고...) 홀수이면 결국 마지막에는 열린 상태(즉, 1인 상태)이기 때문에 n 이하의 숫자 중 해당 수의 약수가 홀수인 수를 구하면 된다.

근데!, 약수의 개수가 홀수인 수는 곧 제곱수 밖에 없다.

🐱‍👤 실제 코드

---

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());

        System.out.println((int)Math.sqrt(N));

    }
}

Math.sqrt는 N의 제곱근을 구하는 수로, 이는 곧 n이하의 제곱수의 개수와도 일치하다.
단, Math.sqrt() 메서드는 double형을 반환하기 때문에 int로 형변환을 해줘야 한다.

🐱‍👤 실제코드 )for문을 이용한

---

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());

        int cnt = 0;
        for(int i = 1; i * i <=N; i++) {
            cnt++;
        }

        System.out.println(cnt);

    }
}

두 방법에는 큰 차이가 존재하지 않는다.

💜 참고자료

---

백준 13909 창문 닫기 [JAVA]