[Java] 백준 24265번: 알고리즘 수업 - 알고리즘의 수행 시간 4

문제 url:
알고리즘 수업 - 알고리즘의 수행 시간 4

문제:

🤔 문제 알아보기

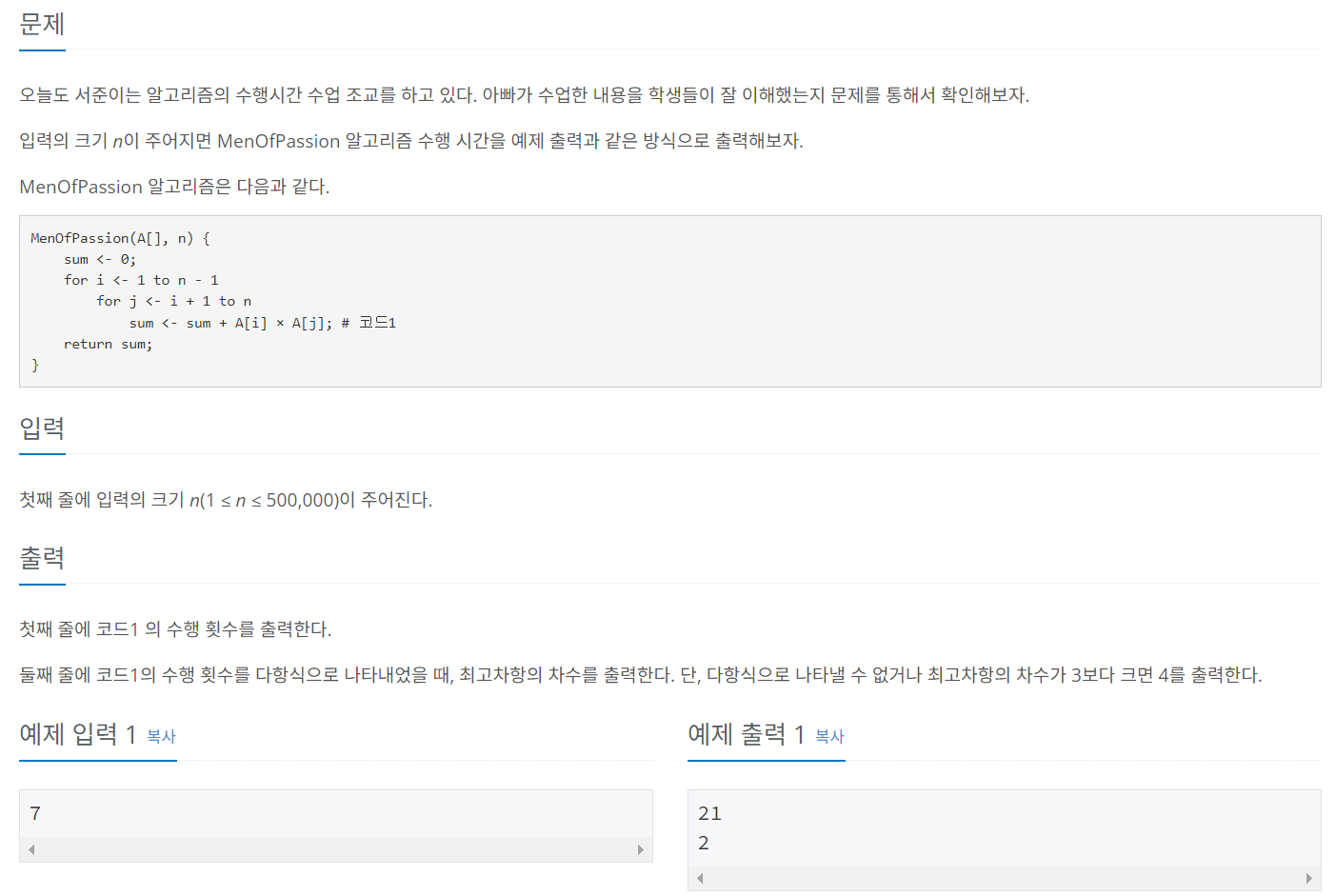
문제의 MenOfPassion 알고리즘을 잘 살펴보면 2중 for문인 것을 알 수 있다.
즉, 이것도 O(N^2)의 시간 복잡도를 가진다.

이걸 가지고 문제를 풀어보니깐. 어라? 수행 횟수가 49가 아니라 21이다.
그럼 이제 MenOfPassion을 곰곰히 살펴보자.

해당 알고리즘을을 java로 나타내보면

int n = 7;
int sum = 0;
for (int i = 1; i <= n-1; i++) {
	for (int j = i = 1; i <= n; j++) {
    	sum++;
    }
}

이런식으로 된다고 볼 수 있다.

이를 표로 나타낸다면

i = 1	i = 2	i = 3	i = 4	i = 5	i = 6
6	5	4	3	2	1
sum = 6	sum = 11	sum = 15	sum = 18	sum = 20	sum = 21

이와 같이 로직이 구성되면서 출력1이 21이 나올 수 있는 것이다.

필자는 못 떠올림 해당 테이블을 보니 떠오르는 무언가가 있지 않은가??
바로 등차 수열이다. 흔히 가우스 합의 공식이라고 불리는
예전에 1부터 100까지 더한 값을 구해라 했던.. 그 문제

등차 수열의 공식은 아래와 같다.
n(n+1) / 2 하지만! 현재 우리는 n이 7이지만, 6까지의 합을 더해야 한다.
그렇다면 n값에는 n-1을 대입할 수 있다.

그러면 (n-1) * (n-1 + 1) / 2 = n(n-1) / 2 이 되는 것이다.
그렇다면 해당 알고리즘의 시간 복잡도는 O(n^2)이 된다.

🐱‍👤 실제 코드

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());

        System.out.println(N * (N-1) / 2);
        System.out.println(2);

    }
}

🤢 회고

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int N = Integer.parseInt(br.readLine());

        long sum = 0;

        for (long i = 1; i< N; i++) {
            sum += i;
        }

        System.out.println(sum);
        System.out.println(2);

    }
}

부끄럽지만, 이를 간과하면 성장할 수 없다고 생각해 이전 코드를 올렸다.
풀이는 등차수열로 풀었지만, 이를 공식화를 떠올리지 못해 저렇게 바보같이 for문을 돌렸다.
수포자로 살아오며 경영학에 사용되는 공식을 공부할 때도, 수학에 대한 무지가 부끄럽지 않았는데, 등차 수열을 못 떠올리는 모습에서 좀 부끄러움을 느꼈다.