문제 url:
알고리즘 수업 - 점근적 표기1
문제:
🤔 문제 알아보기
문제가 굉장히 간단해 보인다. 입력 아래의 tip 문제를 읽어보면 조금 더 이해가 쉬울 것이다.
f(n)은 a1과 a0을 입력받는데, 해당 값에는 a1 n + a0의 값이 저장된다.
또한 f(n) <= c g(n)를 성립해야 한다.
새벽 1시 반에 풀어서 그런가 긁적긁적 일단 이해를 못했다. 근데, 아래 tip을 보고 이해를 하니깐 a1 n + a0 <= c n이면 되는 것 아닌가? 해서
아래의 코드와 같이 풀었다.
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int a1 = Integer.parseInt(st.nextToken());
int a0 = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(br.readLine());
int n = Integer.parseInt(br.readLine());
int fn = a1 * n + a0;
int cgn = c * n;
if(fn <= cgn ) {
System.out.println(1);
} else {
System.out.println(0);
}
}
}
그러니깐 틀렸다고 한다.. 어쩐지 정답율이 낮다고 했다.
필자가 만약 피라미드를 도굴했던 사람이면 진작에 함정에 걸려 해골이 됐을 것이다.
그래서 또 머리 싸메다 타 블로그의 글을 참조하여 코드를 짜보았다.
🐱👤 실제 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int a1 = Integer.parseInt(st.nextToken());
int a0 = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(br.readLine());
int n = Integer.parseInt(br.readLine());
int fn = a1 * n + a0;
int cgn = c * n;
if(fn <= cgn && a1 <= c ) {
System.out.println(1);
} else {
System.out.println(0);
}
}
}
😢 문제 풀이
수학은 끝까지 풀어야 하는데... 왜 풀 때는 모르고 답지를 보면 아! 할까 평생의 숙제이다.
다시 본론으로 넘어가면, 우리는 문제를 꼼꼼하게 읽을 필요가 있다.
문제에 아래와 같은 수식이 있다.
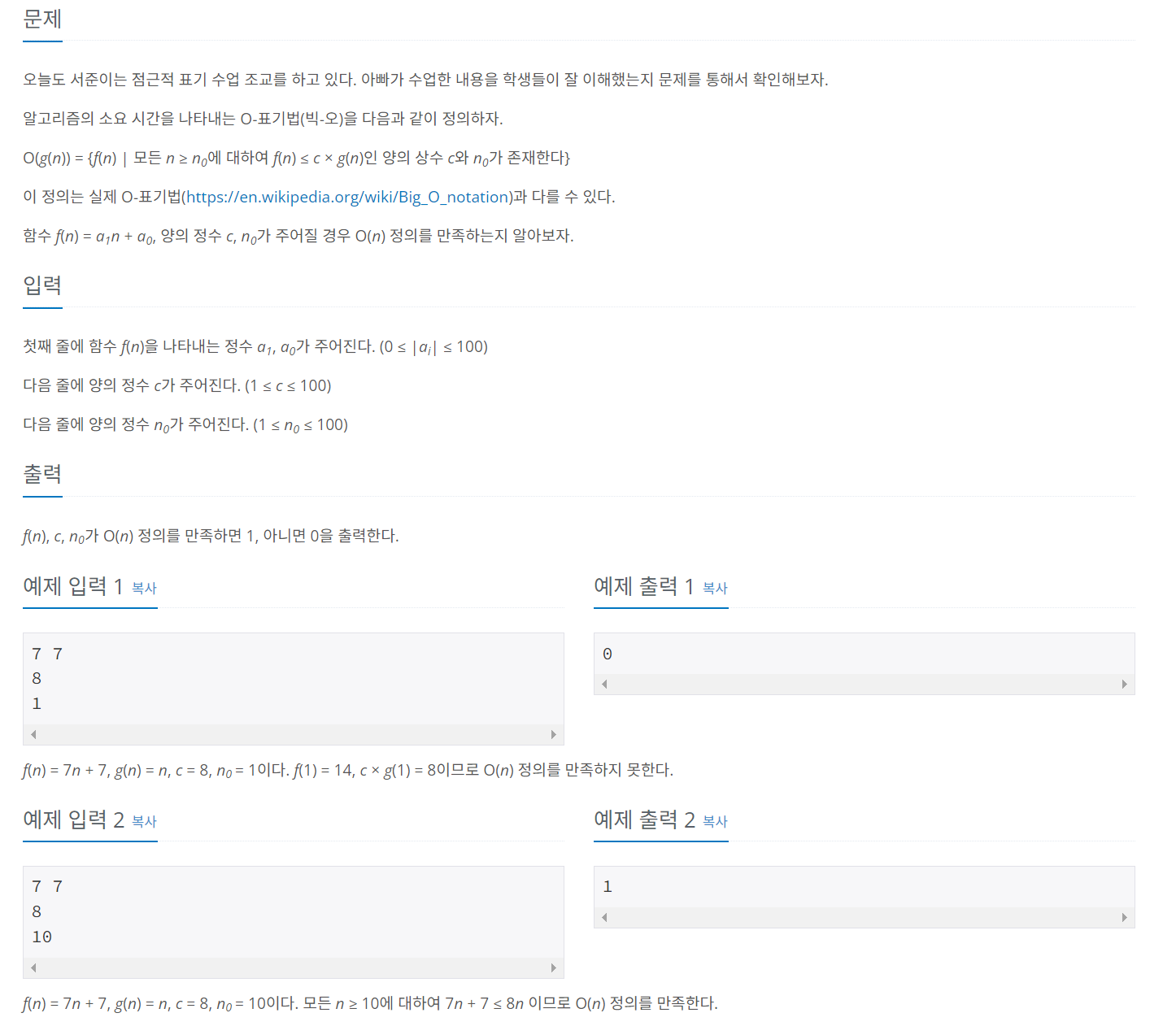
O(g(n)) = {f(n) | 모든 n ≥ n0에 대하여 f(n) ≤ c × g(n)인 양의 상수 c와 n0가 존재한다}
이 글을 조목조목 살펴보면, no는 우리가 양의 정수로 입력을 받는데,
이 값은 n의 최솟값이라는 것을 알 수 있다.
즉, n은 n0보다 크거나 같은 수로,
n0가 10이라면, n은 10부터 시작하여 .... n까지 존재한다는 의미이다.
그렇다면 f(n) ≤ c × g(n)의 의미를 파악해보자면, f(n)의 값은 무조건 c * g(n)의 값보다 작거나 같아야 한다는 의미이다. n에 어느 값이 들어가든지 해도.
그런데 여기서 중요한것은, 입력값에 존재한다.
첫째 줄에 함수 f(n)을 나타내는 정수 a1, a0가 주어진다. (0 ≤ |ai| ≤ 100)
바로 해당 말이다. c와 n0는 양의 정수를 받지만 a1, a0는 정수를 입력받는다. 즉 양수 혹은 음수의 값을 가진다는 의미이다.
그렇다면 왜 이것이 중요한 것인가?
-
먼저 a1이 음수이고 a0이 음수일 때를 가정하자.
이건 굳이 풀이를 안해도a1 * n + a0 <= c * n에서 우항(c * n)이 무조건 클 수 밖에 없는 구조이다. -
a1이 음수이고 a0가 양수일 때를 가정하자,
이것 역시 굳이 풀이를 하지 않아도 a1은 n의 곱을 가지기 때문에 a1이 음수이고 n의 값이 한없이 커지다면. 계속 음수를 가져a1 * n + a0 <= c * n해당 수식이 무조건 성립한다. -
a1이 양수이고 a0가 양수일 때를 가정하자,
해당 문제는 풀이가 조금 필요하지만, 간단하다.
a1 * n + a0 <= c * n해당 수식에서 a1과 a0가 양수라면, 해당 수식은 참과 거짓밖에 존재하지 않는다. 작거나 같거나 혹은 크거나.
이게 무슨말인지는 다음 가정에서 같이 풀어가보겠다.
a1이 양수이고 a0가 음수일 경우
해당 가정법 때문에 정답율이 낮은 것이다. 필자도 생각 못했다..
하나의 예시를 두고 설명하겠다
a1 가 5이며 a0가 -3일 때
C는 3이며 n0가 1이라고 가정하면n >= n0이기 때문에 n은 1부터 시작한다.
n = 1일 떄,
5 * 1 -3 <= n * 2 -> 2 <= 3이기 때문에 참이다.
n = 2일 때,
5 * 2 -3 <= n * 2 -> 7 <= 6이기 때문에 거짓이다.
분명 같은 공식인데, 한개는 참이고 한개는 거짓이다.
그렇다 이러한 문제가 발생하기 때문에 아래의 조건을 만족하지 못하는 것이다.
O(g(n)) = {f(n) | 모든 n ≥ n0에 대하여 f(n) ≤ c × g(n)인 양의 상수 c와 n0가 존재한다}
분명 1일 때는 참인데, 2일 떄는 거짓이라니.. 문제를 풀기 위해서는 이런 부분을 예외처리를 해줄 필요가 있다
그렇다면 a0이 음수라도 항상 좌항이 크거나 혹은 항상 우항이 좌항보다 크거나 같은 경우를 만드려면
a1의 값이 c보다 작거나 같으면 되는 것이다.
이를 풀이해보자면,
a1와 c가 같은 값을 가진다면, a0가 음수이기 때문에 항상 좌항이 큰 값을 가지므로 항상 0을 출력한다.
반대로 a1이 c보다 작은 값을 가진다면, 좌항(a1 * n + a0)이 우항(c * n)보다 항상 작거나 같기 때문에, 아래 조건이 항상 성립할 수 있는 것이다.
O(g(n)) = {f(n) | 모든 n ≥ n0에 대하여 f(n) ≤ c × g(n)인 양의 상수 c와 n0가 존재한다}
작은 경우는 만약 4n -1 <= 4n 이라 가정하면, -1(a0)때문에 늘 작거나 같다.🤢 회고
하... 조금만 더 고민하면 풀 수 있는 문제인데, 수학적 머리가 부족한 것인지 머리가 굳어서 그런것인지. 사실 조금 자책을 하게 된 문제이다.
사실 a1, a0가 음수가 들어갈 수 있는 사실을 알고 있었고 이를 코드화 시켰지만, 문제를 좀 더 생각하고 풀지 않아서 풀지 못했다.
이제는 문제를 조금 더 읽어보고 생각하는 연습을 하며 능력을 길러가야겠다.