문제 url:
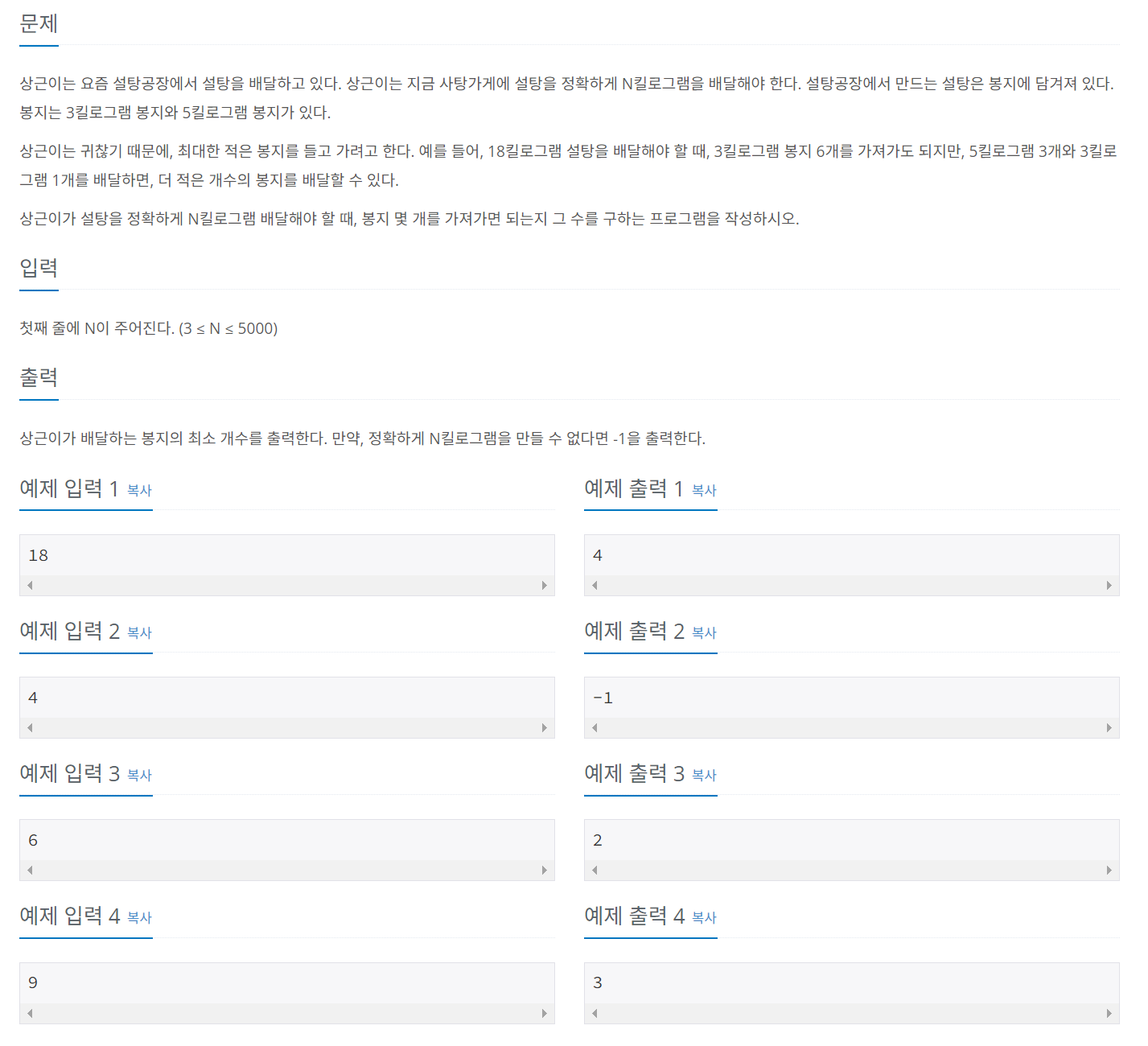
설탕 배달
문제:
🤔 문제 알아보기
문제 자체는 간단해보인다. 실제로 풀어보니 헬이다 문제에 대해 간략히 알아보면,
- 정확히 N크기 만큼 배달하는데, 가장 적게 봉지를 가져가고자 한다.
- 봉지는 5kg, 3kg 이 존재
- 만약 N이 18이라면,
3Kg 6개로 가져가도 되지만, 적게 가져가기 위해서는 5Kg 3개 3Kg 1개 총 4개로 가져가야만 한다.- 그리고 정확하게 Nkg만큼 소분하지 못한다면 -1을 출력하는 문제
그렇다면, N을 5로 나누었을 때, 나누어 떨어지지 않는다면 (ex. 15처럼 딱 떨어지지 않는다면)
3키로를 하나 카운트 한 다음, 5로 나누어지는지 확인하는 작업을 반복하면 구할 수 있을 것이다.
이 말이 무슨말인지를 설명하자면,
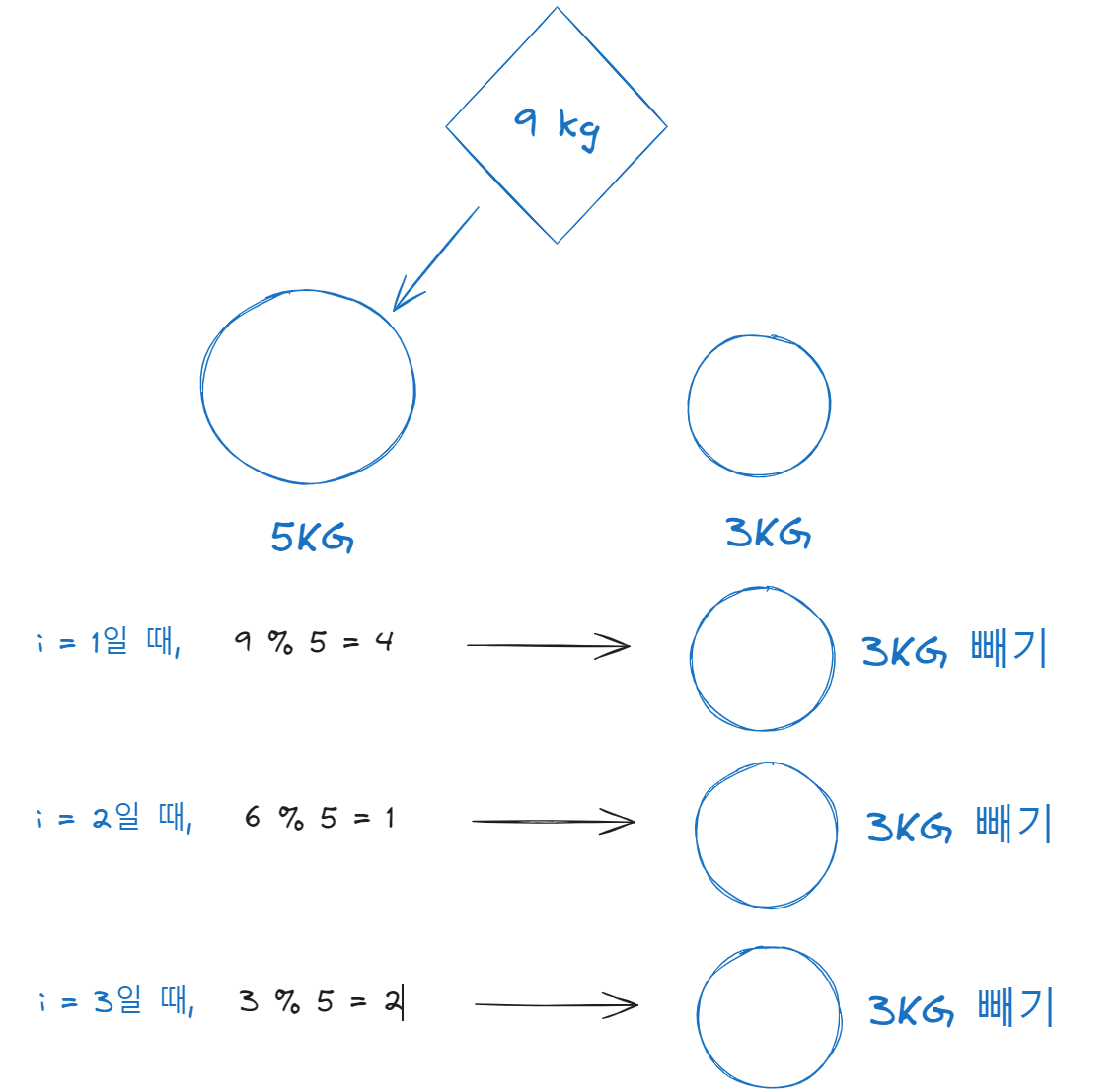
N이 9인 테스트 케이스를 보여준다면, 위의 그림처럼 나타낼 수 있다.
i는 그저 반복하고 있음을 알릴 뿐이다. 코드와는 상관 없다.이런식으로, 봉지를 최소로 가져갈 수 있는 5kg으로 나눠을 때, 떨어지지 않는다면 3kg를 한개씩 담는다는 얘기이다.
N이 9인 경우는 아래와 같이 나눌 수 있다. 그렇다면 N이 18인 테스트 케이스는 어떨까?
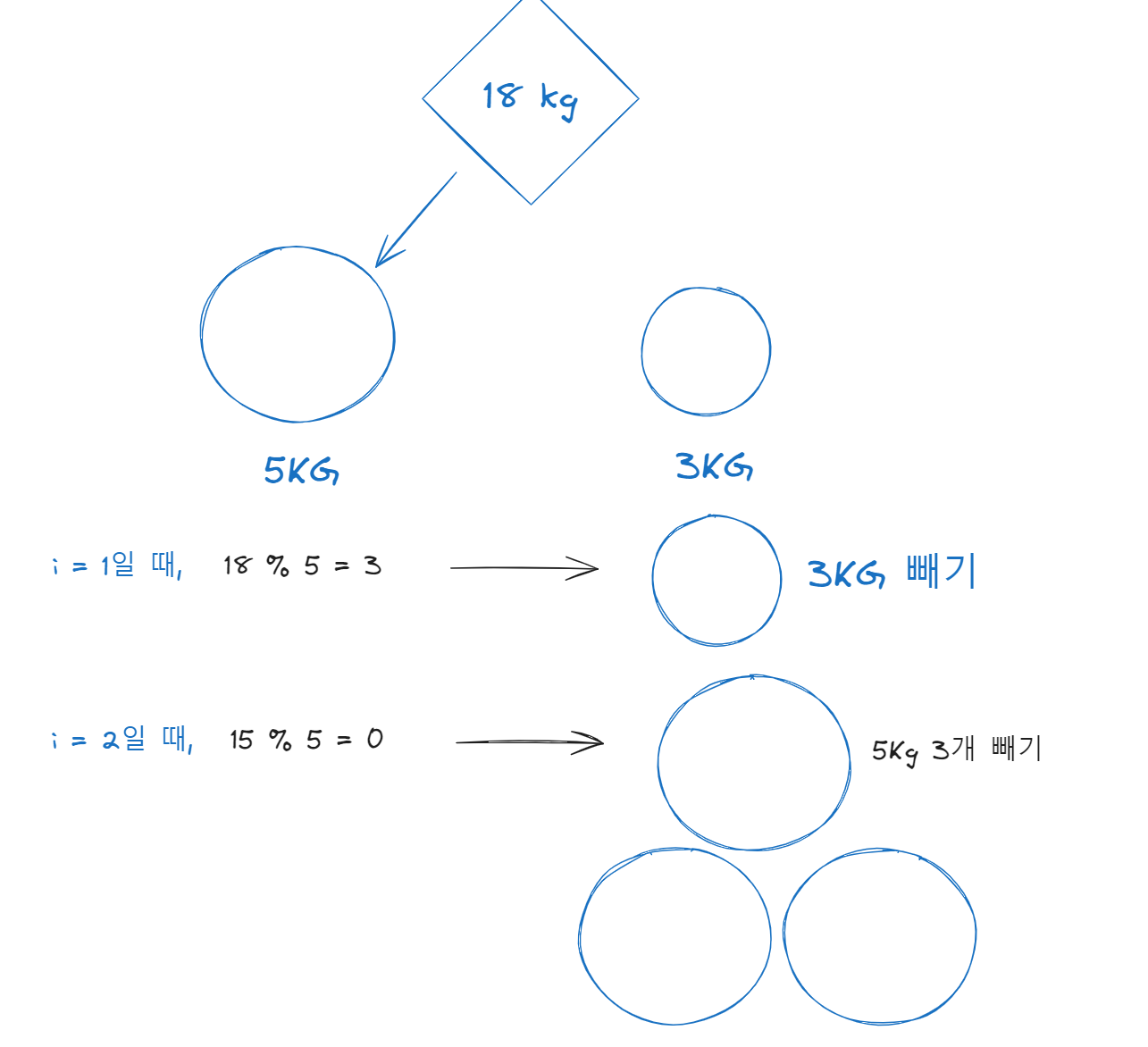
다음과 같이 18은 5로 나누어 떨어지지 않기 때문에 3을 뺀 후 다음값과 비교했을 때, 15는 5로 나누어 떨어져서 값을 구할 수 있는 것을 볼 수 있다.
이번에는 반례로 7을 구해보자, 7은 5로도 3으로도 나누어 떨어지지 않는 값이다.
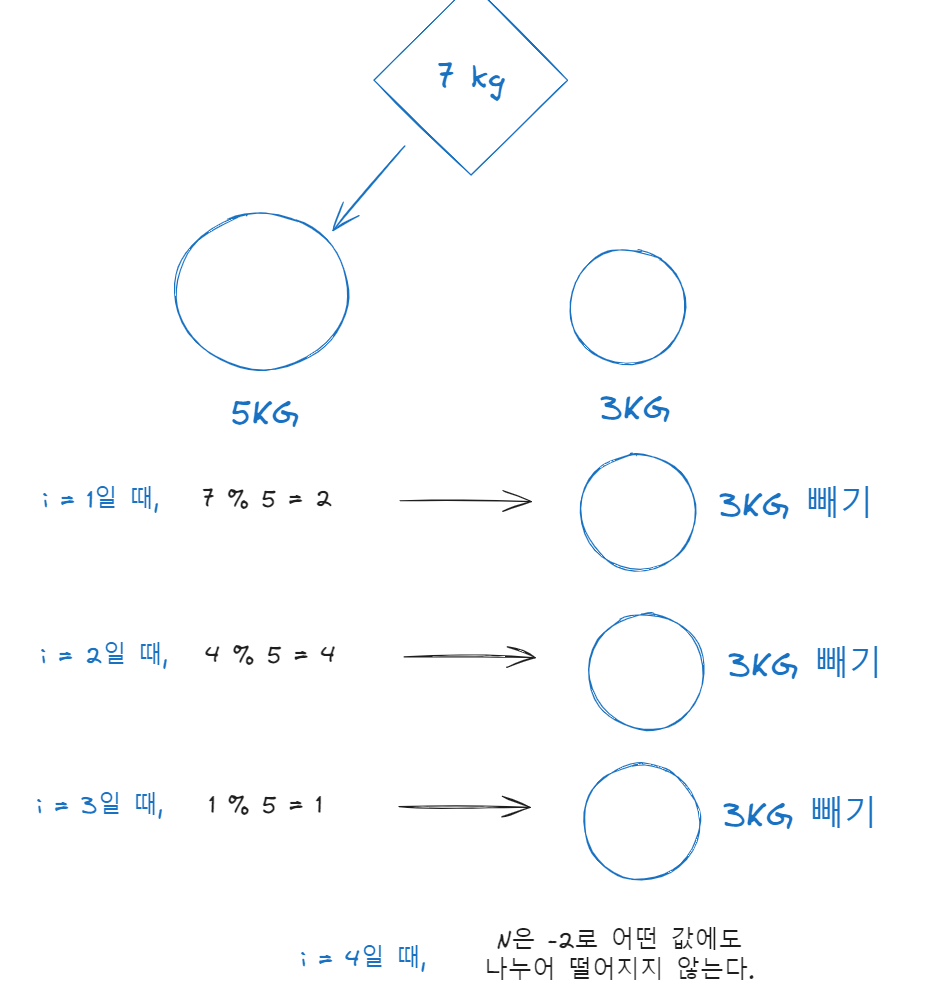
그림이 이해가 안된다면 코드를 같이 살펴보자
🐱👤 실제 코드
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br= new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int count = 0;
while(true) {
// N이 5로 다 나눠지거나 N이 0일 때 반복문에서 벗어남
if(N % 5 ==0) {
count+= N /5;
break;
// N이 0보다 작아지면 -1을 넣기.
// (즉, 크기가 알맞지 않다는 얘기)
} else if(N < 0) {
count = -1;
}
// 3키로 1개만큼 카운트 센 후, 총량에 3kg 빼기
N -= 3;
count++;
}
System.out.println(count);
}
}
위의 설명 그대로, N이 5로 나누어 떨어지지 않으면 3을 계속 빼면서 카운트를 세는 로직이며, N이 0보다 작아진다는 건 결국 5kg, 3kg로 소분하지 못한다는 의미기 때문에 조건에 맞게 -1을 출력한 것이다.
🤢 회고
처음에 이렇게 생각하지는 않았다. 오히려 더 어렵게 생각했는데,
해당 값에서 나올 수 있는 모든 경우의 수를 조건을 달아서 계산하여 풀었다.
근데, 그럴 필요 없이 해당 조건이 전부 포함될 수 있는 코드를 짜면 간단한 것이다.
이걸 잘했으면 벌써 네이버 갔지
모든 조건에 만족하는 로직을 구현하며 이를 맞춰보면서 나중에 리팩토링을 했을 때 좀더 유연하고 간단하게 풀 수 있었던 것 같다. 아래는 이전 코드이다.
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int count = 0;
// 5로도 나눠지는데 해당 나머지가 3으로도 나눠질 때, 혹은 5로도 다 나눠지는 경우
if(N / 5 != 0 && N % 5 % 3 ==0) {
count += N / 5;
N %= 5;
count += N / 3;
// 5로는 나눠지는데, 나머지가 3으로 나눠지지 않는 경우.
} else if(N / 5 != 0 && N % 5 % 3 !=0) {
int min_count = 5000;
for(int i = 0; i <= N / 5; i++) {
// N의 값을 5의 배수로(5,10..)나누는데 나눈 후 나머지 값이 3으로 나누어 질 때,
// 21을 생각하면, 3 (7) / 5 (3) 3 (2)로, 5개가 가장 적게 나옴
// 그래서 min을 이용해 비교
if((N - (5 * i)) % 3 == 0) {
int temp_count = 0;
temp_count += i;
temp_count += (N - (5 * i)) / 3;
min_count = Math.min(min_count, temp_count);
}
}
if (min_count != 5000) {
count = min_count;
} else { // 반례가 7인 경우와 같이 둘 다 속하지 않을 떄 -1 출력
count = -1;
}
} else if(N / 5 == 0 && N % 5 % 3 ==0){ // ex) 3
count += N / 3;
} else { //ex) 4
count = -1;
}
System.out.println(count);
}
}
위의 코드와 비교하면 머리가 아플 것이다.
- 첫 번째 조건식은 18과 같이 5로도 나눠지며, 3으로로도 나눠지는 경우
- 두 번쨰 조건식은 5로 나눴을 떄, 나머지가 3의 배수가 아닌 경우
- 즉, 11과 같이 5로 나누면 나머지가 1이 남아 3의 배수가 안됨
- 하지만 5 , 6(3이 두개)으로 계산하면 풀리는 값들을 계산하는 조건식
- min_count가 5000인 경우는 N값이 5000으로 그냥 나올 수 없는 수로 초기화 시킨 더미 값(특별한 이유 없이 넣었다)
- 세 번쨰 조건식은 3과 같이 5로 나누어 지지는 않지만, 3의 배수인 경우
즉 3을 위한 조건식이다. - 나머지는, 4와 같이 둘 다 나누어 지지 않는 경우를 의미.
찾아보면 반례가 더 나올 수 있겠지만, 찾아볼 수 있는 조건은 아마 다 계산한 것 같다.
필자는 이러한 삽질은 좋아하지 않지만, 개발자는 이러한 삽질속에서 잔근육을 키운다는 얘기를 들어 최대한 삽질속에서 많은 것을 얻고자 노력하는 바이다.