[Java] 백준 2903: 중앙 이동 알고리즘

문제 url:
중앙 이동 알고리즘

문제:

🤔 문제 알아보기

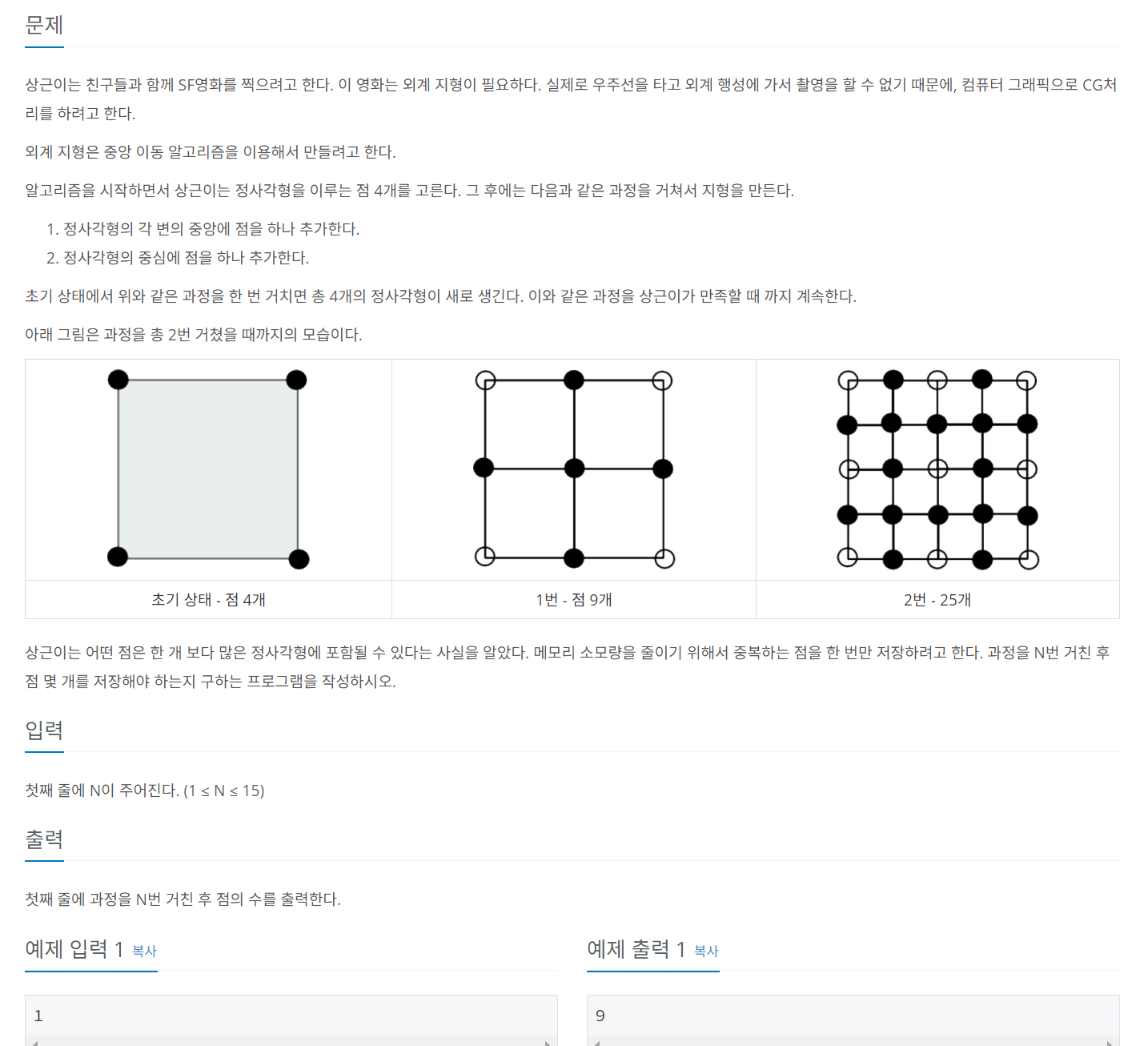
• 정사각형을 이루는 점 4개 -> 각 변에 점 한개씩 그리고 중앙에 점 하나를 추가해서 9개
  • 처음에는 4개 그 다음은 9개 그 다음은 25개 그 다음은 81개
  • (81개를 그렸는데 그림이 너무 안좋아서 지웠다. )
• 총 점의 개수는 n ^ 2 만큼 증가하는 것을 볼 수 있다.
• 2 ^ 2 -> 3 ^ 2 -> 5 ^ 2가 되기 위해 2에서 +1 3에서 +2가 될 수 있도록 코드를 짜보자
• 그렇게 되면 n번만큼 반복을 돌면서 2에다가 누적합으로 1,2,4,8...을 넣은 다음 해당 값의 제곱을 나타내면 답이 될 수 있다.

😎 준비하기

1. BufferedReader를 이용해 입력을 받는다.
2. 몇번 째를 나타낼 것인지를 묻는 변수 N을 생성(해당 값은 반복문에 사용)
3. 초기 값 2를 넣을 변수 d 생성
4. 1, 2, 4, 8.. 누적합을 더할 반복문 생성
5. 제곱한 값을 int형으로 변환 후 출력

🐱‍👤 실제 코드

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        // 2. 반복할 횟수
        int n = Integer.parseInt(br.readLine());

        // 3. 초기값 점 저장
        int d = 2;

		// 4. 1, 2, 4, 8 누적합을 더할 반복문
        for (int i = 1; i <= n; i++) {
            d = (int) (d + Math.pow(2, i-1));
        }

		// 5. 제곱한 값을 int형으로 변환
        int result = (int)Math.pow(d,2);
		
        System.out.println(result);

        br.close();

    }
}

🤢 회고

다시 한번 수학적 지식이 많이 부족하다는 것을 느끼고 있다. 이런 문제에서 빠르게 규칙성을 찾는 연습이 많이 필요하다는 것을 느꼈다.

위의 방법대로 푸니깐. 시간이 많이 걸렸다. 그래서 더 나은 방법을 찾아나섰고 역시나 좋은 코드는 구글에 많이 존재하였다.

반성하는 마음으로 코드 리팩토링

import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        // 1. 반복할 횟수
        int n = Integer.parseInt(br.readLine());

        // 2. 2^ 2, 3^2, 5^2, 9^2승은 곧 (2^n+1) ^ 2승의 값과 같다.
        // 여기서 n은 아까 입력받았던 위의 n과 동일
        System.out.println((int)Math.pow(Math.pow(2,n)+1,2));

        br.close();
    }
}

• 2^2승은 ((2 ^n) +1)) ^ 2승과 같다. 이게 무슨말??
• 2^2승은 첫 값이기 때문에 n이 0과 같을 것이다.
  • 그렇다면 2 ^ 0승은 1과 같기 때문에 1 + 1은 2가 될 수 있다.
  • 이를 반복하면 3 ^ 3승은 n이 1이기 때문에 2 ^ 1 = 2에다가 + 1 해서 3이 나온다.
• 이렇게 풀면 위의 반복문도 없애고 코드도 줄일 수 있다. 역시 머리는 써야 제맛