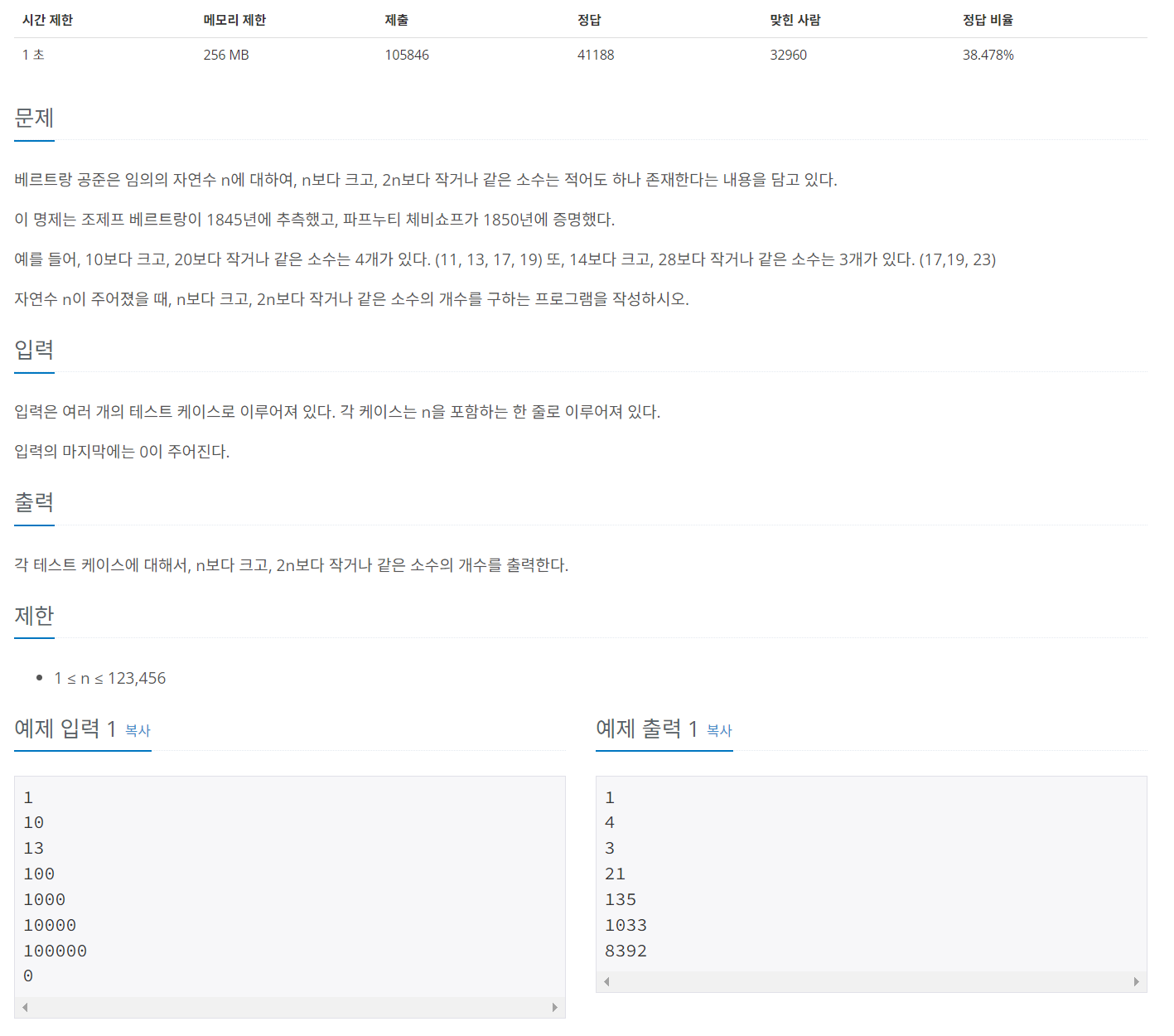
문제 url:
베르트랑 공준
문제:
🤔 문제 알아보기
문제 제목을 보면 무언가 어렵고 힘든 느낌이 들지만, 문제를 읽어보면
이전 백준 1929번: 소수 구하기 문제랑 거의 차이가 없다.
이번 문제도 역시 범위내 소수구하기 문제로, 이번에는 n< p <=2n의 범위안에 존재하는 소수의 개수를 묻는 문제이다.
n의 값이 123,456으로 이중for문을 사용하는 브루트포스 알고리즘보단,
소수의 범위 구하는 2<= p <= sqrt(n)를 활용하여 반복문 횟수를 logN으로 줄이던가,
에레토스테네스의 체를 활용해 O(N loglogN)의 시간복잡도로 구할 수 있다.
필자는 두 개를 구해보도록 하겠다.
🐱👤 실제 코드 1) 에라토스테네스의 체
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sbd = new StringBuilder();
while(true) {
int n = Integer.parseInt(br.readLine());
int n2 = n * 2;
if(n == 0) {
break;
}
int cnt = 0;
//에레토스테네스의 체를 이용하며 진행
// 문제 조건이 n보다는 크고 2n보다 작거나 같은 소수라고 했으니
boolean[] prime_num = new boolean[n2 +1];
// 0과 1은 소수가 아니므로 선수로 true값으로 초기화
prime_num[0] = true;
prime_num[1] = true;
/*
* 소수란?
* 소수는 2<= p <= sqrt(n) 범위에서 p의 값이 n에 나누어 떨어지면 소수가 아님
* 나누어 떨어지지 않는다면 소수
* 여기서 i는 배수를 의미, 2의 배수 , 3의 배수
*/
for(int i = 2; i <= Math.sqrt(n2); i++) {
// 이미 체에서 걸러졋기 떄문에 체에 거르는 로직은 뛰어넘김
if(prime_num[i]) {
continue;
}
/*
* 문제 조건이 n보다는 크고 2 * n보다는 작거나 같기 때문에
* 2 * n 역시 소수인지 아닌지 판별할 필요가 있다.
* 여기서 j는 i의 배수에 대한 배수 값들을 의미
* 2의 배수라면 4, 6, 8, 10....
*/
for(int j = i * i; j <= n2; j = j + i) {
prime_num[j] = true;
}
}
//n보다는 크고 2n보다 작거나 같은 수들 중에 소수 개수를 구하는 문제이기 때문,
for(int i = n+1; i <= n2; i++) {
if(!prime_num[i]) {
cnt++;
}
}
sbd.append(cnt).append("\n");
}
System.out.println(sbd);
}
}
특별한 설명들은 주석에 모두 기재해놨기 때문에 주석을 읽어보면 될 것이다.
그럼에도 이해가 안된다면! 댓글을 달거나 백준 1978번 소수 찾기 해당 링크를 통해 확인할 수 있다.
🐱👤 실제 코드 2) 2<= p <= sqrt(N)의 반복
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sbd = new StringBuilder();
while(true) {
int n = Integer.parseInt(br.readLine());
int n2 = n * 2;
if(n == 0) {
break;
}
int cnt = 0;
for(int i = n+1; i <= n2; i++) {
boolean is_prime = true;
for(int j = 2; j <= Math.sqrt(i); j++ ) {
if(i % j == 0) {
is_prime = false;
break;
}
}
if(is_prime) {
cnt++;
}
}
sbd.append(cnt).append("\n");
}
System.out.println(sbd);
}
}
위부터 짧게 살펴보면,
while(true) {
int n = Integer.parseInt(br.readLine());
int n2 = n * 2;
if(n == 0) {
break;
}
n을 입력받으며, 소수를 구할 범위가 n < p <= 2 n이라고 조건이 있었으니
n2라는 변수에 2 n으로 초기화, 그리고 0을 입력받으면 반복을 멈춰야 하기 떄문에 해당 로직을 구현
int cnt = 0;
for(int i = n+1; i <= n2; i++) {
boolean is_prime = true;
for(int j = 2; j <= Math.sqrt(i); j++ ) {
if(i % j == 0) {
is_prime = false;
break;
}
}
if(is_prime) {
cnt++;
}
}조건이 N < p <= 2 * N에 속한 소수를 구하는것이기 때문에
여기서 i는 해당 범위 안에 속한 모든 수를 나타낸다.
is_prime 변수를 통해, 해당 값이 소수인지 아닌지를 판별하며
i를 j로 나누었을 때, 떨어지면 소수가 아니고 아니면 소수이기에 해당 로직을 구현
소수는
2<= p <= sqrt(n)의 범위의 소수를 나누었을 때, 떨어지면 소수가 아니고, 안 떨어지면 소수이다.
그 후, is_prime이 true(소수임)이면 개수를 더해 마지막에 출력하는 로직이다.
이렇게 계산해보니 다음과 같은 결과가 나왔다.

에라토스테네스의 체 : 220ms
sqrt(N) : 884ms역시 소수를 구해야하는 값이 정확히 나온다면, 에라토스테네스의 체가 효율적이다.
🤢 트러블 슈팅
처음에 is_prime을 반복문 밖에 선언을 해서 조금 어지러웠다...
꼭 변수 스코프를 잘 파악해서 선언을 해주는게 중요하다.
또한 두 번째 반복문에서 Math.sqrt(i)도, 처음에는 Math.sqrt(n2)를 했다가 잘 안되어 시간이 조금 걸렸다.. 문제를 풀 때 무엇을 나눌 것인지 정확히 파악하고 코드를 짜는게 중요함을 배웠다.