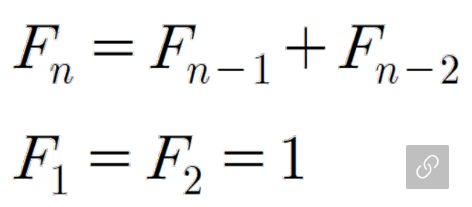🚑 들어가기 앞서
백준을 시작한지 근 보름.. 천천히 백준을 따라풀면서 이제 시간복잡도에 대한 문제가 나오며, 이를 정리하며 배울 필요성을 느껴 정리를 해보고자 한다.
🤔 시간 복잡도란?(Time Complexity)
위키백과에서 해당 용어의 개념을 적어보자면,
컴퓨터과학에서 알고리즘의 시간복잡도는 입력을 나타내는 문자열 길이의 함수로서 작동하는 알고리즘을 취해 시간을 정량화하는 것이다.
-> 이게 뭔 소리인교? 할 수 있다. 그래서 이를 좀 더 쉽게 얘기하자면
다시말해, 해당 알고리즘이 입력으로 받는 데이터의 크기에 따라 얼마나 많은 시간이 소요되는지를 나타내는 지표를 의미한다.
즉, 입력 데이터의 크기를 나타내는 변수(ex. 문자열 길이)에 따라서 알고리즘이 얼마나 효율적으로 동작하는지를 설명한다고 보면 된다.이를 통해서 알고리즘의 효율성을 평가하고 다른 알고리즘과 간의 성능 비교도 가능하다.
※ 다들 아시겠지만, 크기가 클수록 실행 시간은 더 느려진다(길다)
개념을 이렇게 풀이를 해보았고,
이를 한 줄로 표현하자면
'해당 로직의 실행시간을 나타내는 척도'
'입력값과 실행시간의 상관도를 나타낸 것'
으로 정리할 수 있을 것 같다.
🤔 시간 복잡도 표기법
시간 복잡도는 점근적 표기법으로 표현을 많이 한다. 아래의 표기법이 주된 표기법이다.
- Big-O 표기법 / O(N): 빅오 표기법은 알고리즘
최악의 실행시간을 표기 - Ω 표기법 / Ω(N): 오메가 표기법은 알고리즘
최상의 실행시간을 표기 - Θ 표기법 / Θ(N): 세타 표기법은 알고리즘
평균의 실행시간을 표기
이렇게 보면, 세타 표기법이 평균으로 가장 좋은 방법이지 않을까? 생각할 수 있는데,
세타 표기법이 평가하기가 까다롭다고 한다. 그래서 빅오 표기법을 주로 사용한다.
그럼 나 같은 사람은 이제 궁금한게 생긴다. 점근적 표기법이 뭐에요?
💨 점근적 표기법
점근적(기존에는 멀리 있어 보이는 결과물이 근삿값에 점점 가까워지고 있는 상태를 말한다.)즉, 점근적 표기법은 주어진 함수가 존재할 때, 이를 보다 간단한 함수로 만들어 표시한다는 것을 말한다.
누군가 이렇게 쉽게 요약해서 적어놔 가져와 보았다.
자, 그럼 이 말이 무슨말인지 한번 공부해보도록 하자.
먼저, 설명하기 앞서 알고리즘의 실행시간에 대해서 설명하며 차근차근 설명해보겠다.
알고리즘 실행시간은 컴퓨터가 알고리즘 코드를 실행하는 속도에 의존한다.
속도에는 컴퓨터 처리속도, 사용된 언어, 프로그래밍 언어를 컴퓨터가 실행할 수 있는 코드로 바꾸는 컴파일러의 속도 등에 달려있다.
그래서, Java or Python보다는 C/C++이 더 빠르고, AI 학습을 시킬 때, GPU의 연산속도에 따라 학습속도가 차이 나는 것을 볼 수 있다.
이렇게 알고리즘 실행시간은 외부적으로는 다음과 결정될 수 있는데,
내부적으로는 입력값의 크기와 실행 시간의 성장률이 존재한다.
입력값의 크기
간단하게 말하면, 우리가 추천 시스템을 만든다고 가정하면,
일식만 넣고 추천을 돌렸을 때보다 일식, 중식, 양식, 한식, 동남아식 ... 여러 feature를 넣었을 때 더 실행시간이 큰 것을 직관적으로도 알 수 있다.
실행 시간의 성장률
입력값의 크기에 따라 얼마나 해당 함수가 빠르게 커질 수 있는지 입니다.
이를 실행 시간의 성장률(rate of growth)이라고 부르는데,
이때, 프로그램을 쉽게 유지할 수 있도록 불필요한 부분은 제거하고 가장 중요한 부분만 포함해 함수를 간소화 시켜야 합니다.
즉, 계수와 낮은 차수의 항을 제외시킨다는 말과 동일한데.. 필자와 같은 수포자들을 위해 간략히 말하자면
만약 크기 N의 모든 입력에 대한 알고리즘에 필요한 시간이 5n^3 + 3n의 식을 가진다고 한다면, 해당 알고리즘의 점근적 시간 복잡도는 O(n^3)이라 볼 수 있다.
위의 말을 여기에 대입한다면,
계수: 어떤 변수에 곱해지는 인자 -> 여기서는 n^3의 계수는 5이다.
차수: 단항식 안에 포함된 문자 인수(因數)의 개수
즉. 변수 "n"이 거듭제곱되는 수를 의미한다.계수인 5와 낮은 차수인 n ^ 1(3n)을 제외시킨 n^3만 포함시킨다는 얘기이다.
그렇다면 왜 계수와 낮은 차수의 항을 제외시킬까?? 이를 그림과 함께 설명해보겠다.
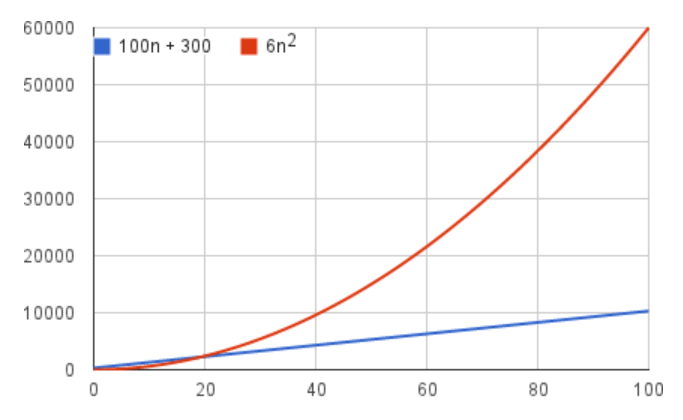
예를 들어 입력값이 n인 알고리즘이 6n^2 + 100n + 300의 수식을 갖는다고 가정하자,
그런 다음 6n^2 와 100n + 300을 비교하면,
n값이 대략 20이 넘어가는 시점부터 6n^2의 값이 100n + 300보다 커지는 것을 확인할 수 있다.
(6 * 400 = 2400) > (100 * 20 + 300 = 2300)
결국 해당 알고리즘의 실행시간은 n^2으로 점점 커지는 것을 확인할 수 있다.
그럼 0.6n^2 + 1000n + 3000을 가지고 비교를 해보자.
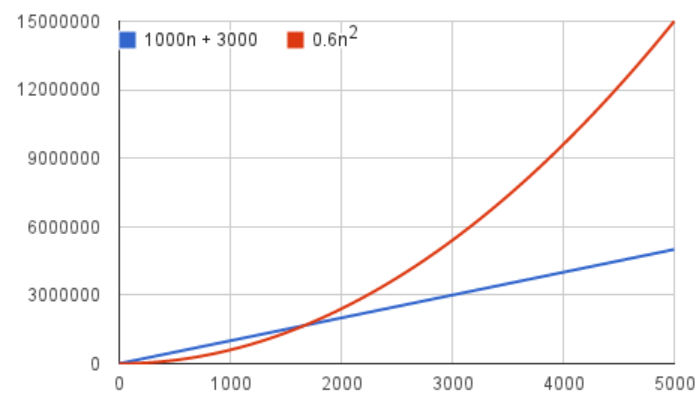
이전 그래프에 비해서 n의 크기는 커졌지만, 결국 두 그래프 역시 빨간색이 파란색을 교차하는 교차점은 존재하는 것을 볼 수 있다.
그래서 중요하지 않는 계수와 차항을 제외하면 이해를 방해하는 부분이 없어져
알고리즘의 실행시간에 중요한 성장률에만 집중할 수 있는 것입니다.
결론을 내리자면, 불필요한 계수와 항을 제거해 알고리즘 실행 시간에 중요한 성장률에만 집중한 것을 점근적 표기법(asymptotic notation)이라 부릅니다.
자! 이제 그러면 아까 위에서 말했던 점근적의 개념과 주어진 함수가 존재할 때, 이를 보다 간단한 함수로 만들어 표시 가 살짝 이해가 된다.
불필요한 부분을 덜어내어 간단히 성장률만 집중하도록 해, 알고리즘의 실행시간에 가까워지게 나타낸 표기법이라 필자는 정의할 수 있을 것 같다.
정확한 의미를 아시는 분은 댓글로 남겨주시면 참고해서 수정해보겠습니다.💦 빅오 표기법(Big-O)
자 이제 빅오 표기법에 대해서 알아보도록 하자,
여기서 필자와 같이 왜 빅오 표기법을 쓰는가? 에 대해서 의문을 가질 수 있다.
위에서 간략히 했었지만, 그래도 이해가 안되서 찾아보았다.
머리 아프다... 찾아봤지만, 글을 적을 용기가 생기지 않는다.
아직 배부른 돼지인 필자는 우리의 친구 gpt한테 도움을 구했고, 그 결과
유연성: 빅오 표기법은 알고리즘의 성능에 대한 상한선을 제시합니다.
이는 입력 크기가 충분히 큰 경우에 알고리즘의 실행 시간이나 공간 사용량이 최악의 경우에
해당하는 것을 보장합니다.
최악의 경우 고려: 빅오 표기법은 최악의 경우에 대한 성능을 나타내므로,
알고리즘이 어떤 상황에서도 일정한 성능을 보장하는지에 대한 정보를 제공합니다.이러한 답변을 해주었다.
그러다, 블로그 글들을 탐방하다가 유연성부분에서 이해를 쉽게 시켜준 글이 있어 가져와봤다.
빅오 표기법(최악)은 알고리즘 효율성을 상한선 기준으로 표기
오메가(최상)는 하한선, 세타(평균)는 상한선과 하한선 사이를 기준으로 표기※여기서 알고리즘 효율성은 그래프가 위로 갈수록, 값이 클수록 비효율적이라 한다.)
만약 등산을 갔다고 하자, 필자가 정상을 오르고 있는데, 너무 힘들어서 정상까지 몇분 걸리냐고 물어봤는데.
누가봐도 등산 못하게 생긴분(빅오)에게 물어보니 1시간 정도 걸린다고 한다.
그 다음 누가봐도 등산 잘하게 생긴분(오메가)에게 물어보니 15분 정도 걸린다고 하자.그럼 우리는 대충 15분에서 1시간 정도 사이(세타) 걸린다고 생각할 수 있다.
이를 빅오 표기법으로 이해하면 오늘밤 때려죽어도 1시간안에 정상에 도착한다고 생각할 수 있다.그래서! 빅오 표기법을 사용하는 것이다.
또한 상한선이 꼭 최악은 아니다. 왜?
1시간안에 도착한다는 것이지, 1시간이 걸린다는 것이 아니기 때문이다.
서론이 너무 길었다. 이제 본론으로 넘어가보자,💢 빅오 표기법 복잡도 비교
우리는 특정 함수 x에 대한 빅오를 찾을 때, 아까 점근적 표기법때 배웠던 (최고차항 외 다른 항 무시, 계수 무시)를 한 최고차항에 대해서만 찾습니다.
※최고차항은 현재 n의 값을 가장 빠르게 증가시키는 항
그래서 빅오 표기법의 복잡도는 N을 통해서 비교할 수 있는데, 아래의 그림이 빅오 표기법에서 나타낼 수 있는 복잡도의 예시입니다.
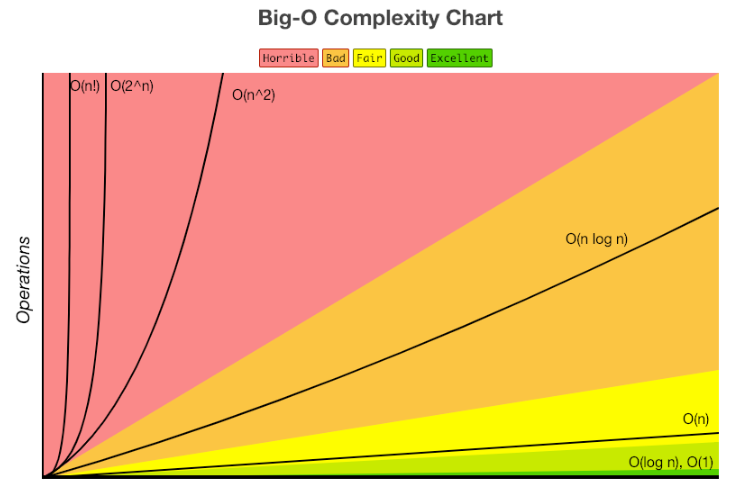
그런데, 아까 그래프가 올라갈수록 효율성이 떨어진다고 했다. 그렇다면 실행시간이 크다는 의미인데 왜 여기는 y축이 time(시간)이 아니라 Operation(연산)일까?
답변:
실행시간은 컴퓨터 하드웨어나 프로그래밍 언어에 따라 차이가 존재하기 때문에 연산 횟수로 나타내는 것이다.
이제 그래프를 보고 실행시간이 빠른순으로 나열하면 아래와 같다.
[빠름] O(1) < O( log n ) < O(n) < O(n log n) < O(n^2) [느림]
이제 하나씩 비교를 해보자,
O(1)
O(1)은 상수 시간이라 불리며 가장 적은 복잡도를 가진다.
O(1)은 문제를 해결하는데, 단 한 단계만 처리해서 1인 것이다.
즉, 입력 데이터 크기에 상관없이 언제나 일정한 시간이 걸린다.
O(log n)
O(log n)은 로그 시간이라 불리며 O(1)보다는 복잡하지만, 다항식보다는 복잡하지 않는다.
O(log n)은 밑이 2인 log2 n을 의미하는데, Big-O 표기법에서는 log 밑의 숫자는 중요하지 않다고 한다. 의미에 큰 영향을 주지 않기 때문이다.
또 O(log n)은 log2 n을 의미한다고 했는데, 이는 이진 로그로 불리는데
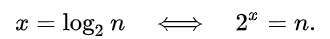
아래와 같은 수식을 가진다. 즉, 2의 거듭제곱의 역함수가 곧 log2 n인 것이다.
그래서 해당 복잡도는 이진탐색일 때 자주 사용된다.
O(n)
O(n)은 선형 시간이라 불리며 입력 데이터의 크기에 비례해서 처리 시간이 걸린다.
즉, n이 1만큼 커지면, 처리 시간도 1만큼 커진다고 보면 된다. 데이터 크기와 시간이 1:1 비례
주로 for문에서 볼 수 있는 시간 복잡도이다.
O(n log n)
O(n log n)은 선형 로그 시간이라 불리며
보통 정렬을 할 때 사용(퀵 정렬, 합병 정렬, 힙 정렬)
흔하게 사용하는 sort() 메서드가 O(n log n) 시간 복잡도를 가진다.
O(n^2)
O(n^2)는 2차 시간이라 불리며, 입력 데이터 n만큼 반복하는데, 또 그 안에서 n만큼 반복한다.
데이터가 적을 땐 모르지만, 많아지면 기하급수적으로 크기가 커진다.
주로 2중 for문에서 볼 수 있다.
O(2 ^ n)
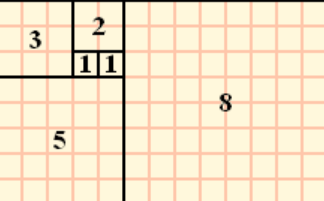
O(2^n)은 지수 시간이라 불리며 피보나치 수열로 비유할 수 있다.
피보자치:
이런식으로 1에서 시작해, 한 면을 기준으로 정사각형을 만든다.이를 공식으로 나열하면,
이렇게 될 수 있다. 즉, fn은 이전 두 수의 합으로 정의되는 수열이다.
이를 자바로 표현하면 이렇게 될 수 있다.
public int fibonacci(int n, int[] arr) {
if (n <= 0 ) {
return 0;
} else if (n == 1) {
return arr[n] = 1;
} else {
return arr[n] = fibonacci(n-1 , arr) + fibonacci(n-2, arr);
}
즉 코드로 보면 재귀함수로 마지막 else문에는 2번씩 함수가 호출되는 것을 볼 수 있다.
그런 다음 n의 값이 1과 0이 될 때까지 반복하기 때문에 O(2 ^ N)의 시간 복잡도를 가지는 것이다.
🤢 정리 후 회고
시간 복잡도를 하루만에 정리한다는 것은 너무 무리였다. 너무나도 양이 방대하기 때문에 여기까지 마무리하고 추후 계속해서 업데이터 및 분리해서 또 블로그에 정리하는 방식으로 이루어 나가도록 해보겠다