happy_quokka.log

happy_quokka.log

[Kalman Filter] (1) 1차원 kalman filter

happy_quokka·2024년 3월 8일

0

Robotics

목록 보기

1/1

Kalman Filter란?

1960년대 루돌프 칼만이 개발한 알고리즘
칼만 필터는 시스템의 상태에 대한 확률적인 정보를 가지고 노이즈가 섞인 측정값과 예측값을 효과적으로 결합하여 상태를 추정
칼만 필터는 센서를 통해 측정한 값에 노이즈가 포함되어도 이 노이즈를 제거
연산 과정이 빠르기 때문에 실시간, 임베디드 시스템에 적합

Kalman Filter 사용 조건

motion model과 observation model이 linear한 경우
motion model과 observation model이 가우시안 분포를 따를 경우

motion model
- 로봇이 현재 위치에서 control input을 받아서 이동했을 때의 확률 모델
observation model
- 로봇이 현재 위치에서 센서를 통해 자신의 위치를 측정했을 때의 확률 모델

Kalman Filter의 전체 과정

칼만 필터는 상태 예측 (state prediction)과 측정 업데이트 (measurement update)를 반복적으로 수행하며 현재 상태를 계산
- 상태 예측 (state prediction): 이전 상태의 추정값과 모델을 이용하여 다음 상태 예측
- 측정 업데이트 (measurement update): 예측값과 실제 측정값을 비교하여 상태를 업데이트

로봇의 경우 로봇이 이동하기 위해서 어디에 있는지 위치를 정확하게 알아야하는데 이때 칼만 필터를 사용
- 상태 예측: 이전 로봇의 파라미터(위치) + 로봇 모션 입력 -> 현재 로봇 파라미터 예측
- 측정 업데이트: 예측한 로봇의 파라미터 + 센서(GPS 등)를 통해 얻은 로봇의 위치 -> 로봇 파라미터 값 업데이트

간단 과정

정규 분포로 본 과정

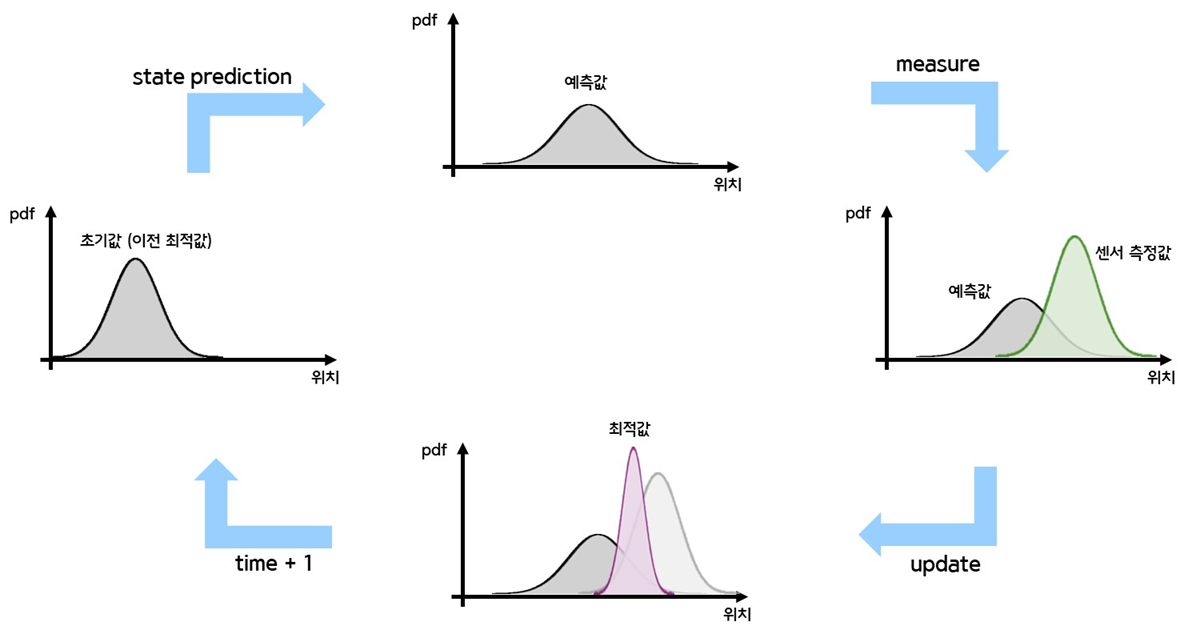
state predict
- 이전 위치에서 motion input을 받아 이동한 현재 위치를 예측하는 과정
- 위치에 대한 정규분포와 이동에 대한 정규분포의 합성곱(convolution) 계산을 통해 이루어진다
measure
- 센서를 사용하여 현재 위치를 측정하는 과정
- 측정한 값도 정규분포로 나타난다
update
- predict를 통해 예측한 값과 센서를 통해 측정한 값을 통해 최적의 값을 계산한다 (예측된 값 갱신)
- 예측값의 정규분포와 측정값의 정규분포의 곱(product) 계산을 통해 이루어진다
time + 1
- 최적의 값을 사용하여 다시 1번부터 수행한다

Kalman Filter 세부 과정

kalman filter를 사용하여 이동하는 로봇의 위치를 추정하는 과정에 대해 자세히 설명한다

0. 로봇의 위치, 이동량 정규분포

칼만 필터에서는 현재 위치와 이동량을 정규분포로 표현할 수 있다
정규분포로 표현하는 이유는 불확실도(uncertainty)를 포함하여 위치, 이동량을 표현하기 위해서이다

로봇의 위치

로봇이 $x=0$ 위치에 있을 가능성이 가장 높다고 가정한다
로봇이 정확하게 $x=0$ 위치에 있을지에 대해 불확실도가 있기 때문에 아래와 같은 정규분포로 표현할 수 있다

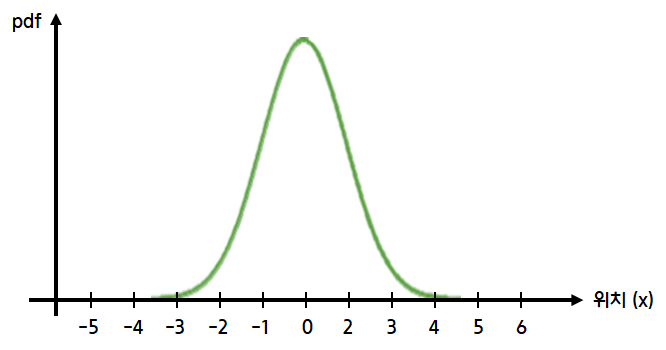
로봇의 이동량

로봇이 $x=3$ 만큼 오른쪽으로 이동한다고 가정한다
이동량 역시 정확하게 $x=3$ 만큼 이동하는지에 대해 불확실도가 있기 때문에 정규분포로 표현할 수 있다

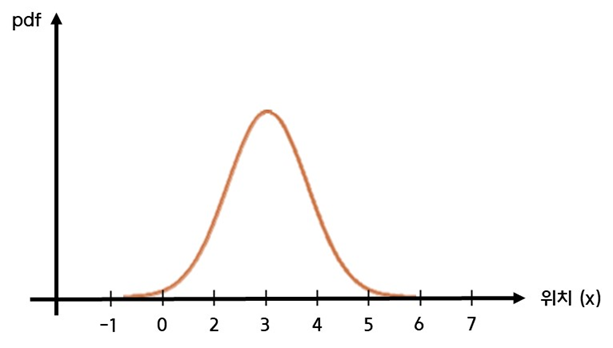
1. State Predict

로봇이 $x=0$ 인 상태에서 $x=3$ 만큼 이동하였을 때 상태를 예측한다
- 로봇이 $x=0$ 인 상태 = 이전 로봇의 파라미터
- $x=3$ 만큼 이동 = motion control input
위치에 대한 정규분포와 이동에 관한 정규분포의 합성곱(convolution) 계산을 통해 예측값을 구한다
- 합성곱을 하는 이유: 물체가 실제로 −∞ 부터 ∞까지 존재할 가능성이 있기 때문에 이 모든 경우에 대해서 이동량의 분포를 곱하고 더해주어야한다 (곱하고 더하는것 = 합성곱)

로봇이 $x=0$ 에서 $x=3$ 만큼 이동했다면 아래와 같은 분포로 표현할 수 있다

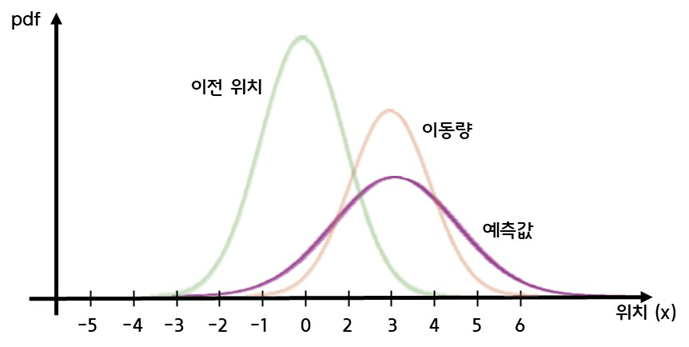
정규분포의 합성곱(convolution) 계산

합성곱은 임의의 두 함수 $f(t)$ 와 $g(t)$ 에 대해 다음과 같이 정의되는 연산이다
(1) $f(t) * g(t) = \int_{-\infty}^\infty f(\tau)g(t-\tau)d\tau$

$f(t), g(t)$ 를 정규분포로 표현하면 다음과 같다 (여기에서 $\mathcal{N}$ 은 정규분포, $\mu$ 는 평균, $\sigma$ 는 분산을 의미한다)
- $f(t)$ 는 $\mathcal{N}_1(x; \mu_1, \sigma_1^2)$
- $g(t)$ 는 $\mathcal{N}_2(x; \mu_2, \sigma_2^2)$

두 함수의 합성곱 결과는 다음과 같다
- (2) $f(t) * g(t) = \mathcal{N}(x; \mu_1 + \mu_2, \sigma_1^2 + \sigma_2^2)$

위의 예시로 보면 $f(t)$ 가 로봇의 위치에 관한 함수, $g(t)$ 가 로봇의 이동량에 관한 함수이고 합성곱 결과는 예측값에 관한 함수이다
예측값 평균은 (2)에 이전 위치 평균인 $\mu_1$ 에 0을 대입하고, 이동량 평균인 $\mu_2$ 에 3을 대입하면 구할 수 있다
- $\mu_1 + \mu_2=0+3=3$
예측값 분산은 (2)에 이전 위치 분산을 $\sigma_1$ 에 대입하고, 이동량 분산을 $\sigma_2$ 에 대입하면 구할 수 있다

여기에서 합성곱 결과 함수도 정규분포를 따르고, 합성곱 결과 함수의 분산은 두 입력 정규분포의 분산보다 항상 크다는 것을 알 수 있다
즉, 합성곱을 수행할 때마다 분산이 증가한다 (=불확실도가 증가한다)

2. Measure

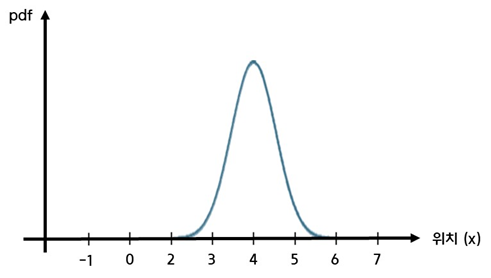
센서를 사용하여 현재 위치를 측정하는 단계이다
센서를 사용하여 측정한 측정값에도 noise, 즉 불확실도가 있기 때문에 정규분포로 표현할 수 있다

센서에서 측정한 로봇의 현재 위치가 $x=4$ 라고 가정하면 아래와 같은 정규분포로 표현할 수 있다

3. Update

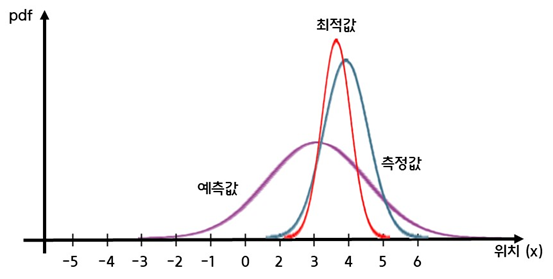
예측값과 측정값을 사용하여 최적값을 구하는 단계이다. 즉, 이전값을 갱신(update)하는 단계이다
이때 베이즈 정리(Bayes' theorem)를 사용하여 예측값 정규분포와 측정값 정규분포의 곱(product) 계산을 통해 최적값을 구한다

최적값 역시 정규분포로 표현할 수 있다
- 두 정규분포(측정값, 예측값)의 곱은 정규분포 모양이지만 정규분포는 아니다
- 하지만 아래의 베이즈 수식에서 볼 수 있듯이 $P(E)$ 를 나누어 정규화를 해주기 때문에 최적값도 정규분포가 된다

그 후 이 최적값이 1번의 predict 과정에서 로봇의 상태(위치)로 사용되고 1번부터 3번이 반복된다

베이즈 정리(Bayes' theorem)

베이즈 정리는 사전 정보(prior)와 관측(likelihood)를 사용하여 사후 확률(posterior)를 계산하는 것으로 이전 정보를 갱신하고 새로운 정보를 통합할 수 있다
베이즈 정리는 불확실성이 있는 상황에서 신뢰도 있는 값을 추정하기 위해 사용된다

칼만 필터는 상태를 확률 분포로 표현하고, 센서로 측정한 측정값도 오차가 있을 수 있다
이런 상황에서 확률 기반으로 값을 추정하는 베이즈 정리를 사용하면 현재 상태 추정에 대한 신뢰도를 표현할 수 있고 기존의 상태 추정과 통합하여 값을 갱신할 수 있다

베이즈 정리 수식

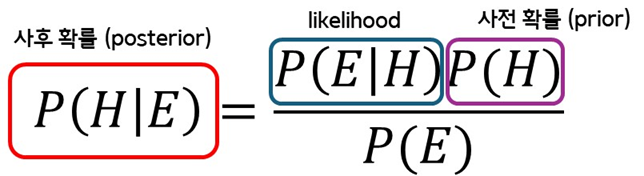
위의 예시(로봇의 위치 추정)에서의 의미
- $P(H|E)$ : 최적값
- $P(E|H)$ : 센서를 통해 측정한 측정값
- $P(H)$ : 예측값 (state predict 과정에서 예측한 예측값)

즉, 최적값을 구하려면 측정값과 예측값의 곱을 계산해야한다

정규분포의 곱(product) 계산

$f(t), g(t)$ 를 정규분포로 표현하면 다음과 같다 (여기에서 $\mathcal{N}$ 은 정규분포, $\mu$ 는 평균, $\sigma$ 는 분산을 의미한다)
- $f(t)$ 는 $\mathcal{N}_1(x; \mu_1, \sigma_1^2)$
- $g(t)$ 는 $\mathcal{N}_2(x; \mu_2, \sigma_2^2)$

정규분포의 곱 결과 분포를 $\mathcal{N}_{new}(x; \mu_{new}, \sigma_{new}^2)$ 라고 하면 그 계산 과정은 다음과 같다
- $\mu_{new} = \frac{\mu_1 \sigma_2^2 + \mu_2 \sigma_2^2}{\sigma_1^2+\sigma_2^2}$
- $\sigma_{new}^2 = \frac{1}{1/\sigma_1^2 + 1/\sigma_2^2} = \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2 + \sigma_2^2}$

위의 예시로 보면 $f(t)$ 가 예측값에 관한 함수, $g(t)$ 가 측정값에 관한 함수이고 곱 결과는 최적값에 관한 함수이다

reference

0개의 댓글