20210616 알고리즘 문제 풀이
백준 4948번 베르트랑 공준
https://www.acmicpc.net/problem/4948

풀이
import sys prime_ox = [True for _ in range(123457 * 2)] for i in range(2, int((123457 * 2) ** 0.5)): if prime_ox[i] == True: for j in range(i + i, 123457 * 2, i): prime_ox[j] = False prime_list = [i for i, j in enumerate(prime_ox) if j == True and i >= 2] num = int(sys.stdin.readline()) while num != 0: answer = 0 for i in prime_list: if i <= num: continue elif num * 2 >= i > num: answer += 1 else: break print(answer) num = int(sys.stdin.readline())
- 모든 원소가 True인 소수 리스트 만들어 주기(prime_ox)
(문제에서 주어진 범위를 미리 설정해놓음)- 반복문을 실행할 때 원소가 True이면 그 수의 배수들에 False를 대입
- prime_list라는 변수를 만들고 그 안에 소수들을 넣어줌
- 입력받은 값(num)이 0이 아니면 num<=i<=2*num인 범위의 소수의 개수를 출력해주는 반복문을 실행하면 원하는 답이 출력됨
백준 1436번 영화감독 숌
https://www.acmicpc.net/problem/1436
풀이
n = int(input()) cnt = 0 six_n = 666 while True: if '666' in str(six_n): cnt += 1 if cnt == n: print(six_n) break six_n += 1
- 666(six_n)이 들어간 숫자의 개수를 세기 위해 cnt라는 변수를 0으로 선언
- six_n을 문자열로 변환했을 때 '666'이라는 문자가 존재하면
cnt에 1을 더해줌- 만약 cnt와 입력받은 값이 같다면 six_n을 출력
- 반복문이 실행될 때마다 six_n에 1을 더해줌
- 예를 들면, n = 1이면 six_n에 '666'이 존재하기 때문에 cnt에 1을 더해준다 > cnt == 1 == n 이므로 six_n을 출력한다.
n = 2이면 위의 과정을 한 번 반복한 후에 666이 한 번 더 나올 때까지 666(six_n)에 1씩 더해주는 반복문을 실행한다. 666이 한 번 더 나오는 경우는 1666이고 그 때 cnt에 1을 더해주고 six_n 값을 출력한다.
입력 1 > 출력 666 / 입력 2 > 출력 1666
백준 2869번 달팽이는 올라가고 싶다
https://www.acmicpc.net/problem/2869
풀이
a,b,v = map(int, input().split()) height = v - a if height % (a - b) == 0: day = int(height / (a - b)) else: day = int(height / (a - b) + 1) print(day + 1)
- 마지막에 올라가야 하는 높이(height)는 전체 높이에서 낮에 올라갈 수 있는 높이를 빼준 값이다.
(height를 올라가는데 걸리는 일수는 1일, 정상에 오르면 내려오지 않기 때문에 마지막에 a만큼 올라가면 끝이다.)
그 높이를 제외하고 계산을 해보면 height를 하루에 올라갈 수 있는 높이로 나눠줬을 때 걸리는 일수가 나온다.- 만약 걸리는 일수가 0으로 나누어 떨어지지 않는다면 1을 더해준다.
- 걸리는 일수에 처음에 제외했던 높이를 올라가는데 걸리는 시간인 1을 더해주면 총 걸리는 일수를 구할 수 있다.
백준 1037번 약수
https://www.acmicpc.net/problem/1037
풀이
N = int(input()) A = list(map(int, input().split())) max_num = max(A) min_num = min(A) print(max_num * min_num)
- 진짜 약수가 모두 주어지기 때문에 가장 작은 값과 가장 큰 값을 곱하면 진짜 수를 구할 수 있다.
백준 2609번 최대공약수와 최소공배수
https://www.acmicpc.net/problem/2609
풀이
import math a, b = map(int, input().split()) print(math.gcd(a, b)) print(math.lcm(a, b))
- 내장함수 math의 gcd,lcm module을 이용한다.
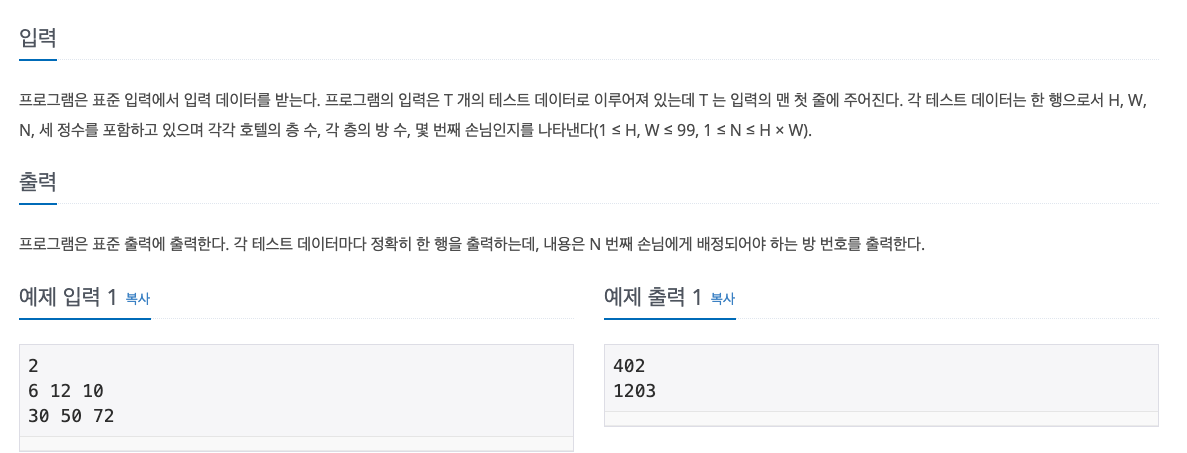
백준 10250번 ACM 호텔
https://www.acmicpc.net/problem/10250

풀이
for _ in range(int(input())): H,W,N = map(int, input().split()) a = N % H b = N // H + 1 if a == 0: a = H # 꼭대기 층 b -= 1 print(a * 100 + b)
- H = 전체 층 수 / W = 각층의 방 수 / N = 몇 번째 손님
- 호텔 정문까지 가장 짧은 거리를 선호하므로 모든 층의 1호를 먼저 채우고 2호,3호...이런 방식으로 객실을 배정해야 한다.
ex ) 101 > 201 > 301 > 102 > 202 > 302....- 손님의 순번(N)을 전체 층 수(H)로 나눈 나머지 값이 배정받을 층 수의 앞자리가 된다.
- 손님의 순번(N)을 전체 층 수(H)로 나눈 몫에 1을 더해주면 배정받을 호 수가 된다.
- 만약 손님의 순번(N)이 전체 층 수(H)와 같은 경우(최상층) 층 수의 앞자리가 0이 되는데 그 경우는 배정받을 층 수의 앞자리에 전체 층 수를 대입해준다. 또한 그 경우에 배정받을 호 수에 1이 더해져서 나오므로 1을 빼줘야한다.
ex ) H = 6 / W = 12 / N = 6일 때
a = N % H = 6 % 6 = 0
a == 0 이므로 a = H = 6
a = 6
b = 6 // 6 + 1 = 2
a == 0 이므로 b -= 1
b = 1
따라서 601이 출력된다.
백준 1929번 소수 구하기
https://www.acmicpc.net/problem/1929

풀이
M,N = map(int, input().split()) prime1 = [] prime2 = [] def big_prime(N): a = [False, False] + [True] * (N - 1) for i in range(2, N + 1): if a[i]: prime2.append(i) for j in range(2 * i, N + 1, i): a[j] = False def small_prime(M): a = [False, False] + [True] * (M - 1) for i in range(2, M): if a[i]: prime1.append(i) for j in range(2 * i, M + 1, i): a[j] = False def answer(M,N): if 1 <= M <= N <= 1000000: big_prime(N) small_prime(M) answer_prime = list(set(prime2) - set(prime1)) answer = sorted(answer_prime) for i in answer: print(i) else: return False answer(M,N)풀이
- 에라토스테네스의 체를 이용해서 N 이하의 소수를 찾아주고 전역 변수인 prime2에 소수들을 추가하는 함수 big_prime(N)을 만들었고, M 미만의 소수를 찾아주고 전역 변수인 prime1에 소수들을 추가하는 함수 small_prime(M)을 만들었다. 문제에서 원하는 것이 M 이상 N 이하의 소수를 출력하는 것이기 때문에 small_prime(M)의 범위를 M 미만으로 설정해주었다.
(차집합을 이용해 리스트를 만들 때 M이하의 소수를 찾아주면 M이 출력되지 않음)- answer 함수는 위의 두 함수를 실행시킨 후 answer_prime이라는 변수에 차집합을 대입해준 후 만들어진 리스트를 정렬하고 원소들을 차례대로 출력해주는 함수이다.

