🎮

문제 설명

제한 사항

• maps는 n x m 크기의 게임 맵의 상태가 들어있는 2차원 배열로, n과 m은 각각 1 이상 100 이하의 자연수입니다.
• n과 m은 서로 같을 수도, 다를 수도 있지만, n과 m이 모두 1인 경우는 입력으로 주어지지 않습니다.
• maps는 0과 1로만 이루어져 있으며, 0은 벽이 있는 자리, 1은 벽이 없는 자리를 나타냅니다.
• 처음에 캐릭터는 게임 맵의 좌측 상단인 (1, 1) 위치에 있으며, 상대방 진영은 게임 맵의 우측 하단인 (n, m) 위치에 있습니다.

입출력 예

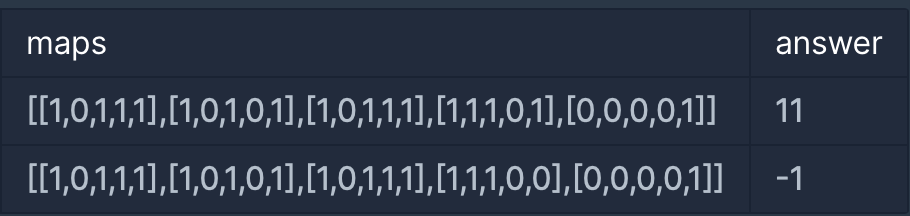
입출력 예 설명

입출력 예 #2
문제의 예시와 같으며, 상대 팀 진영에 도달할 방법이 없습니다. 따라서 -1을 return 합니다.

구현 방법

전형적인 최단거리 BFS 문제이다.

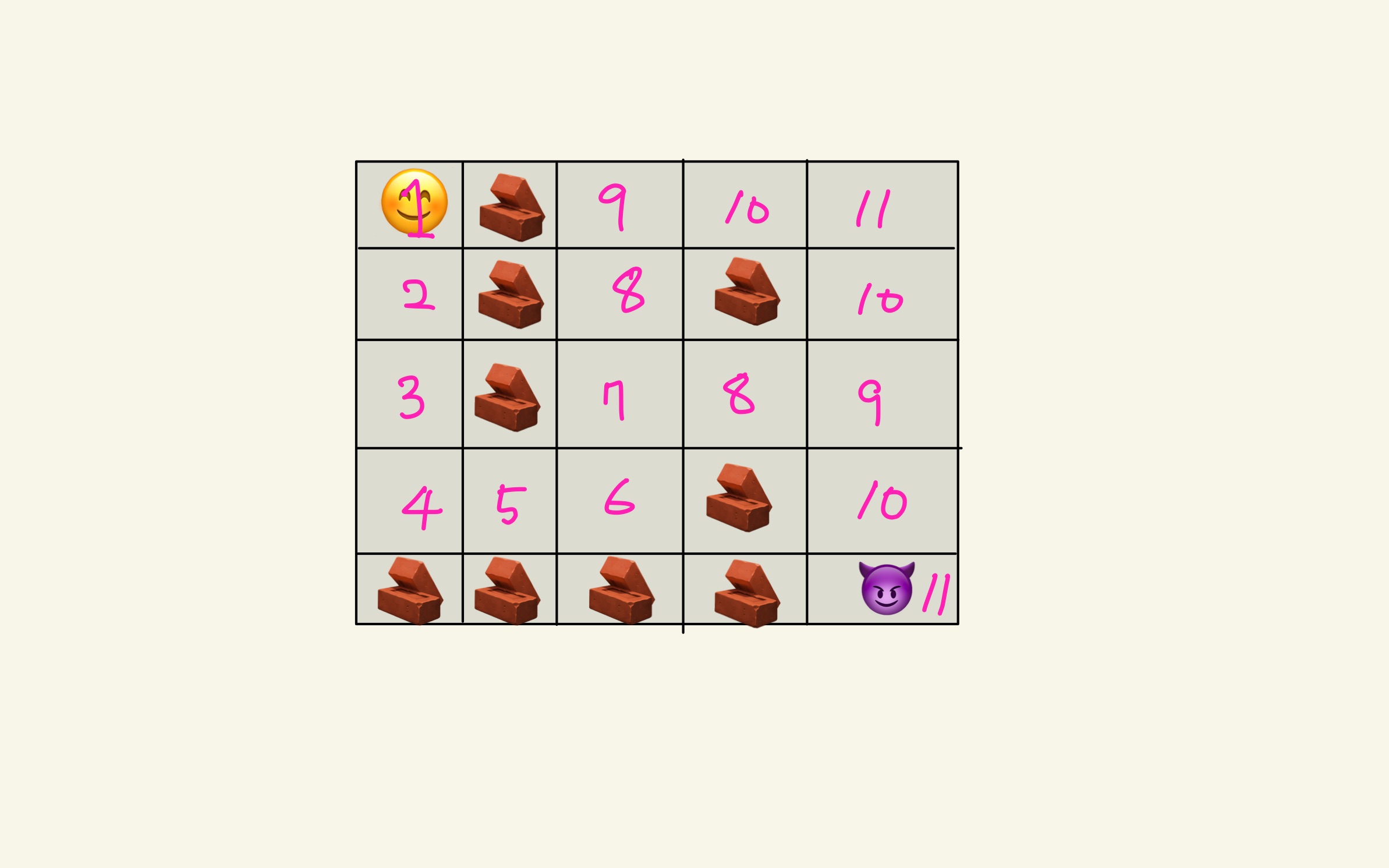
• (x,y,count)를 기준으로 BFS를 돌렸을 때 나타나는 결과 화면이다.
• 분홍색 숫자는 거리를 의미한다.
• 현재 좌표를 기준으로 상하좌우를 탐색하며 아래의 조건에 위배되는 항목은 큐에 넣지 않는다.
• 조건1: 게임 맵 밖에 벗어나는 경우
• 조건2: 이미 방문한 경우
• 조건3: 벽인 경우

CODE

from collections import deque
def solution(maps):
    n,m = len(maps),len(maps[0])
    dx = [1,-1,0,0]
    dy = [0,0,1,-1]
    q = deque([(0,0,1)])
    visited = [[False]*m for _ in range(n)]
    visited[0][0] = True
    while q:
        x,y,cnt = q.popleft()
        if (x,y) == (n-1,m-1):
            return cnt
        for i in range(4):
            nx = x+dx[i]
            ny = y+dy[i]
            
            if (0<=nx<n and 0<=ny<m and not visited[nx][ny]
               and maps[nx][ny]):
                q.append((nx,ny,cnt+1))
                visited[nx][ny] = True
    return -1

주의 사항

아래 코드를 주목해보자.

if (0<=nx<n and 0<=ny<m and not visited[nx][ny]
               and maps[nx][ny]):
                q.append((nx,ny,cnt+1))
                visited[nx][ny] = True

방문 처리를 큐에 집어넣을 때 하고 있다.
평상시 최단 거리 문제를 풀 때 나는 방문처리를 큐에서 팝을 할 때 하는 습관을 갖고 있었다. 여타 문제에서는 그렇게 해도 잘 풀렸으나 이 문제에서는 그렇게 하면 시간 초과에 걸린다. 왜일까?

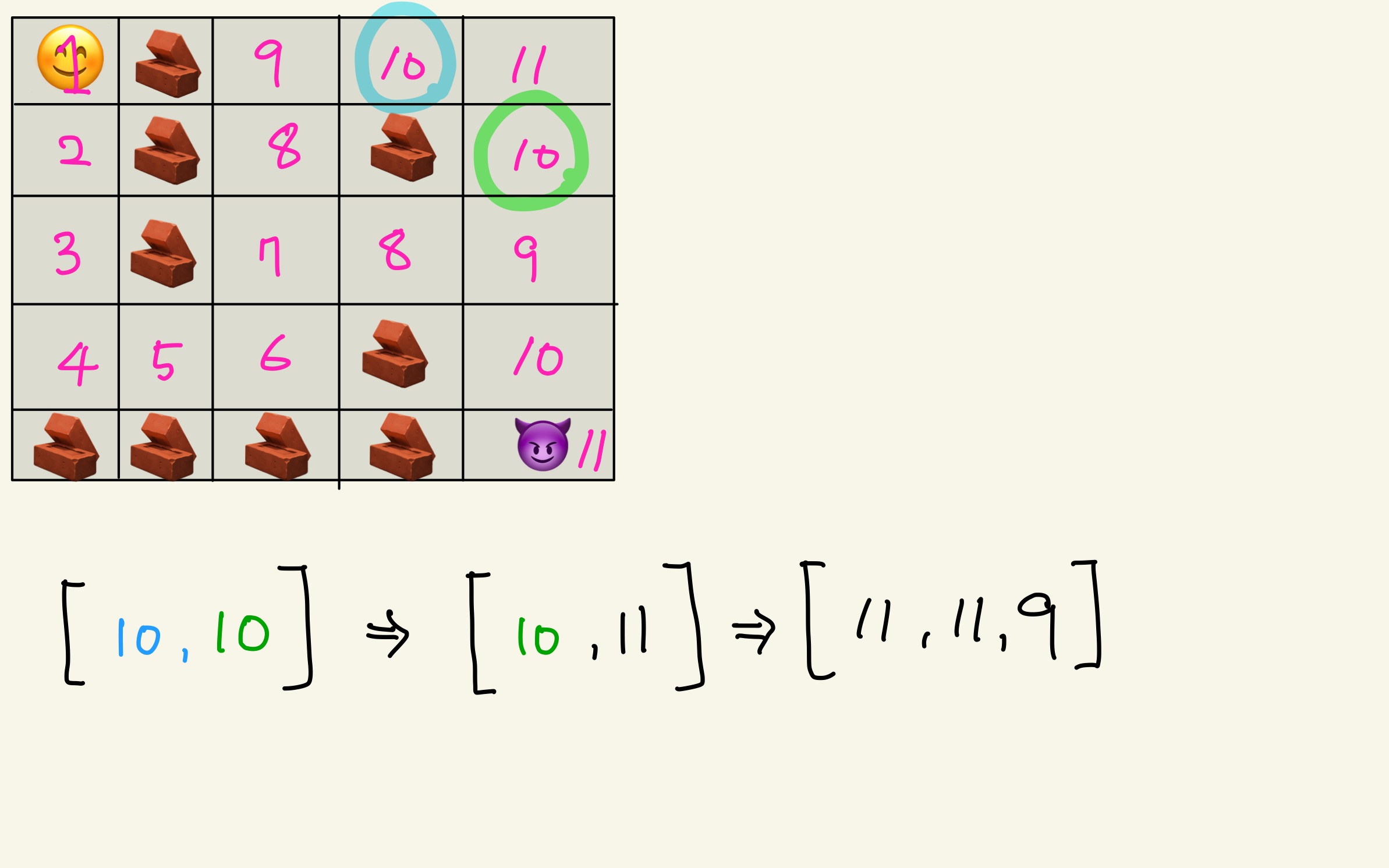
하늘색 10에서 11을 큐에 넣었다. 방문 처리를 큐에서 팝할 때 한다고 가정하면 이 때 11은 큐에서 나오지 않았기 때문에 미방문으로 표시되어있다.
그러므로 초록색 10에서도 11을 큐에 넣는다. 만약 11을 큐에 넣을 때 방문 처리를 했다면 초록색 10에서 11을 넣지 않았을텐데 큐에서 나올때 기준으로 방문 처리를 했기 때문에 이러한 중복 연산이 발생하고 이는 시간 초과를 야기한다.