거리 합 구하기

정말 어려웠다. 결국 해설 강의 참조 😭
다익스트라/플로이드 와샬 두 가지 방법으로 시도해봤지만 실패!

그 이유는 다익스트라는 O(ElogE)의 시간복잡도를 갖는데 이 문제는 모든 노드로부터 다익스트라를 수행해야하므로 O(E^2logE)의 시간복잡도를 갖는다.

대충 연산량이 E^2이라고 해도 최대 연산량은 (4*10^10) = 400억이다.
이 문제의 제한 시간은 6초이므로 대략 6억번 연산 가능한데 400억을 연산하기에 택도 없는 시간제한이다. 따라서 이 문제를 다익스트라 여러번 돌리는 것으로 풀면 시간초과가 발생한다.

플로이드 와샬도 마찬가지로 O(V^3)이므로 시간초과.

따라서 이 문제는 DFS로 풀어야 한다.

풀이

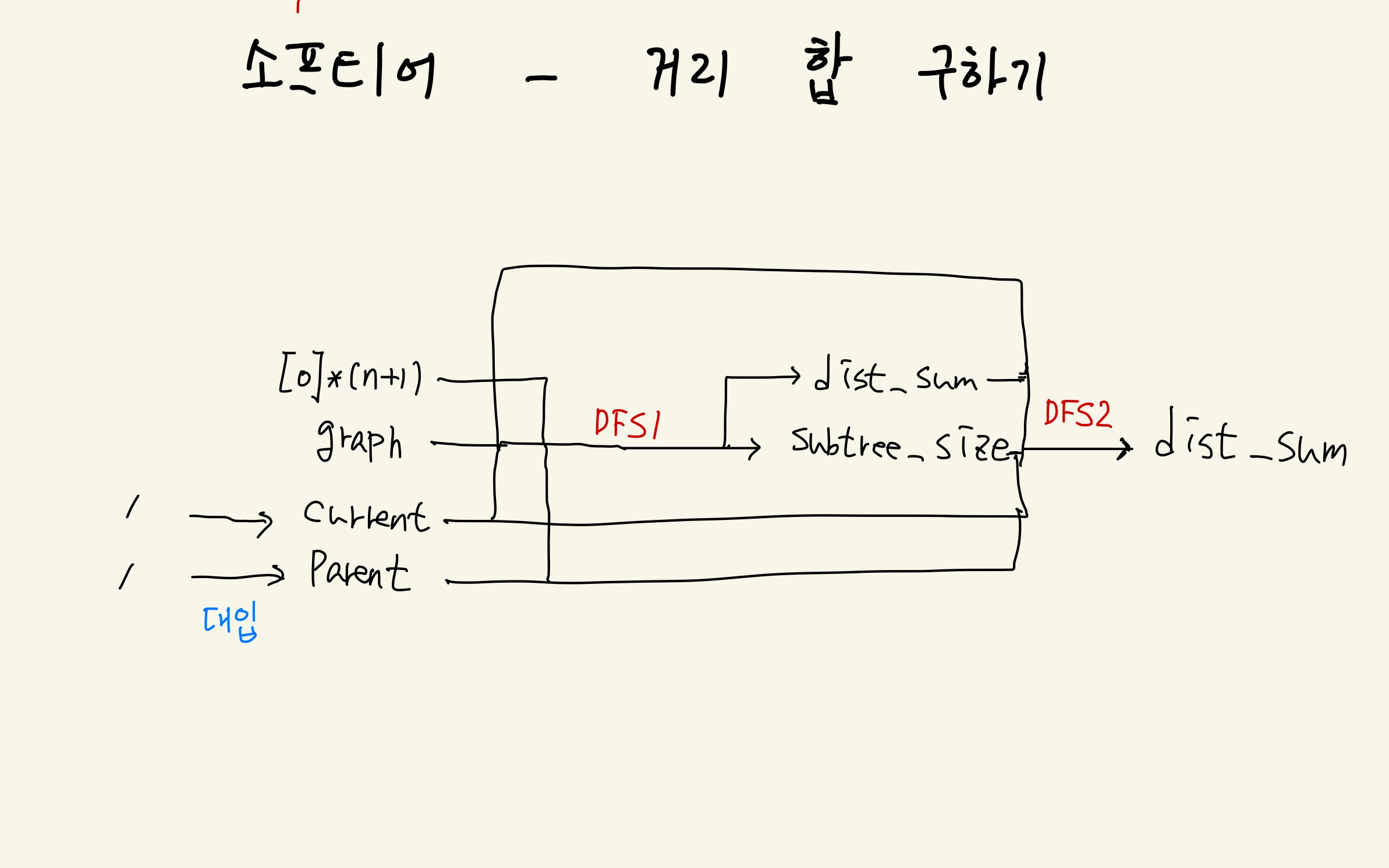
변수

• n: 노드의 개수(초기 조건)
• graph: 양수 weight가 있는 양방향 그래프(초기 조건)
• current: 현재 노드
• parent: 부모 노드
• subtree_size: 자식 트리에 포함 되어 있는 노드 개수
• dist_sum: 각 노드로부터 모든 노드로의 최소 비용 합(문제)

함수

• dfs1: subtree_size 구해주는 함수
• dfs2: dist_sum 구해주는 함수

설명

솔루션 강의

코드

플로이드 와샬(오답)

import sys
input = sys.stdin.readline
INF = int(1e9)

def floyd_warshall(graph):
    for i in range(1,n+1):
        for j in range(1,n+1):
            for k in range(1,n+1):
                if graph[j][k] > graph[j][i]+graph[i][k]:
                    graph[j][k] = graph[j][i]+graph[i][k]
    distance = graph
    return distance

n = int(input())
graph = [[INF]*(n+1) for _ in range(n+1)]
for i in range(1,n+1):
    for j in range(1,n+1):
        if i == j:
            graph[i][j] = 0
for i in range(n-1):
    a,b,cost = map(int,input().split())
    graph[a][b], graph[b][a] = cost,cost
distance = floyd_warshall(graph)

for i in range(1,n+1):
    answer = sum(distance[i][1:])
    print(answer)

DFS(정답)

import sys
sys.setrecursionlimit(10**6)
def dfs1(current,parent,subtree_size,dist_sum):
    subtree_size[current] = 1
    for i in range(len(graph[current])):
        child = graph[current][i][0]
        weight = graph[current][i][1]
        if child != parent:
            dfs1(child,current,subtree_size,dist_sum)
            subtree_size[current] += subtree_size[child]
            dist_sum[current] += dist_sum[child] + weight*subtree_size[child]
    return subtree_size,dist_sum

def dfs2(current,parent,subtree_size,dist_sum):
    for i in range(len(graph[current])):
        child = graph[current][i][0]
        weight = graph[current][i][1]
        if child != parent:
            dist_sum[child] = dist_sum[current] + weight*(n-subtree_size[child]) - weight*subtree_size[child]
            dfs2(child,current,subtree_size,dist_sum)
    return dist_sum

n = int(input())
graph = [[] for _ in range(n+1)]
for _ in range(n-1):
    x,y,t = map(int,input().split())
    graph[x].append((y,t))
    graph[y].append((x,t))
subtree_size,dist_sum = dfs1(1,1,[0]*(n+1),[0]*(n+1))
dist_sum = dfs2(1,1,subtree_size,dist_sum)

for i in range(1,n+1):
    print(dist_sum[i])