당구 연습 🎱
문제 설명
프로그래머스의 마스코트인 머쓱이는 최근 취미로 당구를 치기 시작했습니다.
머쓱이는 손 대신 날개를 사용해야 해서 당구를 잘 못 칩니다. 하지만 끈기가 강한 머쓱이는 열심히 노력해서 당구를 잘 치려고 당구 학원에 다니고 있습니다.
오늘도 당구 학원에 나온 머쓱이에게 당구 선생님이"원쿠션"(당구에서 공을 쳐서 벽에 맞히는 걸 쿠션이라고 부르고, 벽에 한 번 맞힌 후 공에 맞히면 원쿠션이라고 부릅니다) 연습을 하라면서 당구공의 위치가 담긴 리스트를 건네줬습니다. 리스트에는 머쓱이가 맞춰야 하는 공들의 위치가 담겨있습니다. 머쓱이는 리스트에 담긴 각 위치에 순서대로 공을 놓아가며 "원쿠션" 연습을 하면 됩니다. 이때, 머쓱이는 항상 같은 위치에 공을 놓고 쳐서 리스트에 담긴 위치에 놓인 공을 맞춥니다.
머쓱이와 달리 최근 취미로 알고리즘 문제를 풀기 시작한 당신은, 머쓱이가 친 공이 각각의 목표로한 공에 맞을 때까지 최소 얼마의 거리를 굴러가야 하는지가 궁금해졌습니다.
당구대의 가로 길이 m, 세로 길이 n과 머쓱이가 쳐야 하는 공이 놓인 위치 좌표를 나타내는 두 정수 startX, startY, 그리고 매 회마다 목표로 해야하는 공들의 위치 좌표를 나타내는 정수 쌍들이 들어있는 2차원 정수배열 balls가 주어집니다. "원쿠션" 연습을 위해 머쓱이가 공을 적어도 벽에 한 번은 맞춘 후 목표 공에 맞힌다고 할 때, 각 회마다 머쓱이가 친 공이 굴러간 거리의 최솟값의 제곱을 배열에 담아 return 하도록 solution 함수를 완성해 주세요.
단, 머쓱이가 친 공이 벽에 부딪힐 때 진행 방향은 항상 입사각과 반사각이 동일하며, 만약 꼭짓점에 부딪힐 경우 진입 방향의 반대방향으로 공이 진행됩니다. 공의 크기는 무시하며, 두 공의 좌표가 정확히 일치하는 경우에만 두 공이 서로 맞았다고 판단합니다. 공이 목표 공에 맞기 전에 멈추는 경우는 없으며, 목표 공에 맞으면 바로 멈춘다고 가정합니다.

위 그림은 친 공이 벽에 맞았을 때의 움직임을 나타낸 그림입니다. 치기 전 공의 위치가 점 A입니다.

위 그림은 친 공이 꼭짓점에 맞았을 때의 움직임을 나타낸 그림입니다. 치기 전 공의 위치가 점 A입니다.
제한사항
- 3 ≤
m,n≤ 1,000 - 0 <
startX<m - 0 <
startY<n - 2 ≤
balls의 길이 ≤ 1,000 balls의 원소는 [a, b] 형태입니다.- a, b는 머쓱이가 맞춰야 할 공이 놓인 좌표를 의미합니다.
- 0 < a <
m, 0 < b <n - (a, b) = (
startX,startY)인 입력은 들어오지 않습니다.
입출력 예
| m | n | startX | startY | balls | result |
|---|---|---|---|---|---|
| 10 | 10 | 3 | 7 | [[7, 7], [2, 7], [7, 3]] | [52, 37, 116] |
입출력 예 설명
입출력 예 #1
첫 번째 예시의 첫번째 공에 대한 그림은 다음과 같습니다.

당구대의 좌측 하단 좌표가 (0, 0) 입니다.
점 A는 머쓱이가 칠 공이 놓인 위치입니다.
점 A → 점[0] : 점선을 따라 이동하면 거리의 제곱이 52로 최소가 됩니다.
같은 예시의 두 번째 공에 대한 그림은 다음과 같습니다.

점 A → 점[1] : 점선을 따라 이동하면 거리의 제곱이 37로 최소가 됩니다.
- 점 A에 놓인 공을 왼쪽 방향으로 x축과 수평이 되도록 보내면 벽에 맞고 점 [1]에 닿아 이동 거리가 더 짧아보이지만, A가 벽으로 이동하는 경로에 점 [1]이 있으므로, 벽에 맞기전에 공에 먼저 맞게 됩니다.
같은 예시의 세 번째 공에 대한 그림은 다음과 같습니다.

점 A → 점[2] : 점선을 따라 이동하면 거리의 제곱이 116으로 최소가 됩니다.
따라서 [52, 37, 116]을 return 합니다.
※ 공지 - 2023년 3월 20일 문제 난이도가 Lv. 1 → Lv. 2로 변경되었습니다.
설계
def solution(m, n, startX, startY, ball):
answer = []
flag = ['up','down','left','right']
for i in range(len(ball)):
tmp = INF
for f in flag:
tmp = min(tmp,cushion(m,n,startX,startY,ball[i][0],ball[i][1],f))
answer.append(tmp)
return answer당구대 상하좌우 쿠션 경로 길이를 계산하여 제일 최소값을 구한다.
꼭지점 쿠션은 고려하지 않는다.
왜냐하면, 꼭지점 쿠션보다 작은 원쿠션이 항상 존재하기 때문이다.
get_dist
def get_dist(p0,p1):
return abs(p0[0]-p1[0])**2+abs(p0[1]-p1[1])**2두 점 p0와 p1의 거리를 구해주는 함수.
단, 루트는 벗겼다. 왜냐하면 컴퓨터에서 소수점 에러가 발생하기 때문이다.
또한 최종 정답에서 제곱을 할 예정이기 때문에 상관 없다.
cushion
시작점(x0,y0)으로부터 타겟점(x1,y1)까지의 원쿠션 거리를 반환해주는 함수이다.
- 입사각 / 반사각
- 대칭점
두 가지를 이용해서 풀었는데 1번은 틀린 풀이고 2번이 정답 풀이다.
틀린 풀이부터 설명하면서 어떠한 실수를 범했는지 소개하도록 하겠다.
입사각 / 반사각 (틀린 풀이)
def cushion(m,n,x0,y0,x1,y1,flag):
if flag == 'up':
if y1 >= y0 and x0 == x1:
return INF
cshn_pnt = (min(x0,x1) + ((n-y0)*abs(x0-x1))/(2*n-y0-y1),n)
if flag == 'down':
if y1 <= y0 and x0 == x1:
return INF
cshn_pnt = (min(x0,x1)+((y0*abs(x0-x1))/(y0+y1)),0)
if flag == 'left':
if x1 <= x0 and y0 == y1:
return INF
cshn_pnt = (0,max(y0,y1)-((x0*abs(y0-y1))/(x0+x1)))
if flag == 'right':
if x1 >= x0 and y0 == y1:
return INF
cshn_pnt = (m,max(y0,y1)-((m-x0)*abs(y0-y1))/(2*m-x0-x1))
a = get_dist((x0,y0),cshn_pnt)
b = get_dist(cshn_pnt,(x1,y1))
return a+b+2*((a*b)**0.5)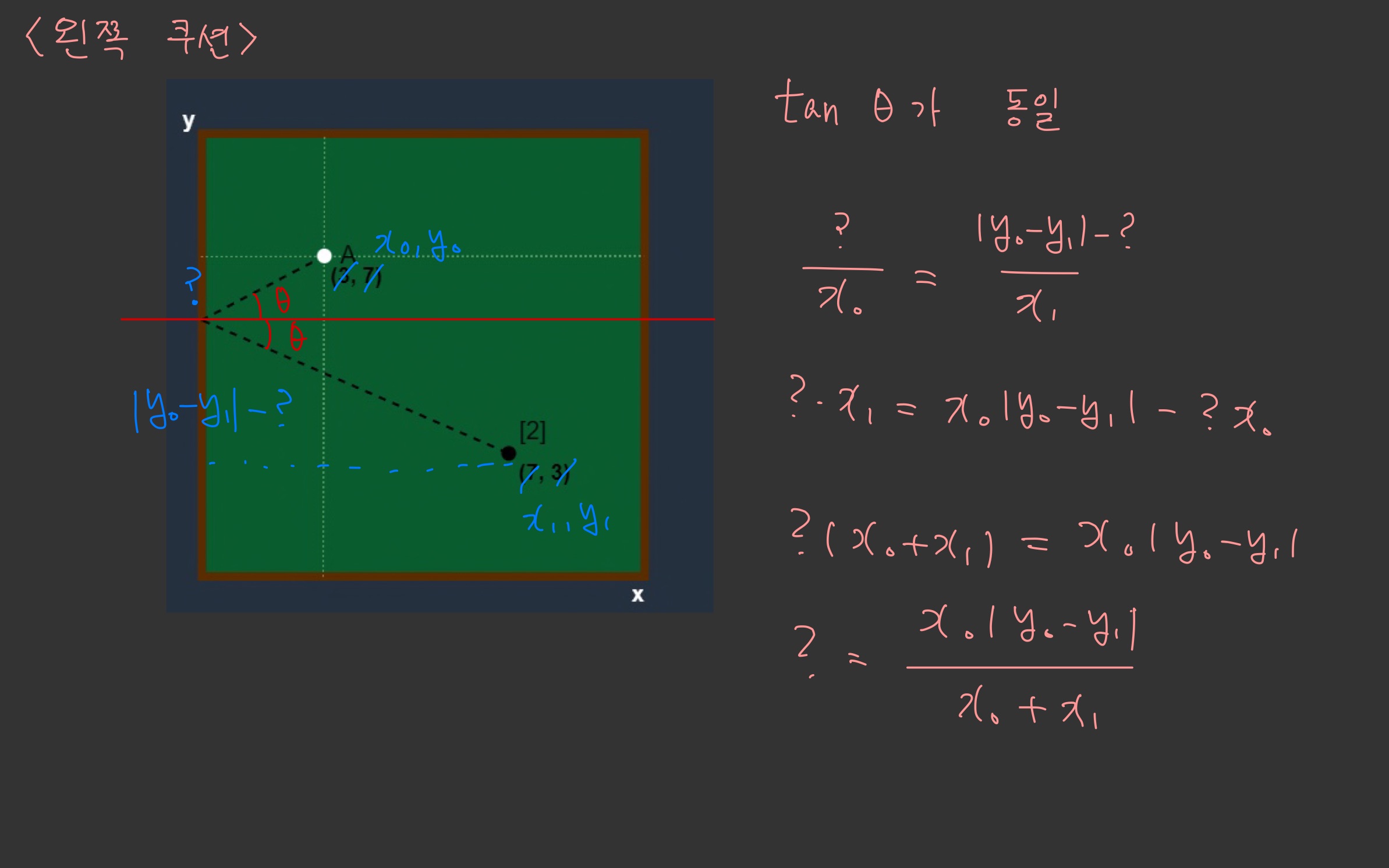
왼쪽 쿠션을 치는 경우를 생각해보자.
입사각과 반사각이 같으므로 탄젠트 값도 같다.
따라서 위의 수식과 같이 우리는 ? 값을 알아낼 수가 있고 이를 통해 쿠션 포인트의 좌표값을 알 수 있다.
그러면 우리는 "시작점, 쿠션점, 타겟점" 이 세가지를 알고 있으므로
[시작점 ➡️ 쿠션점 거리 + 쿠션점 ➡️ 타겟점 거리]^2 으로 정답을 도출해낼 수 있다.
하지만 이는 치명적인 문제가 있다.
바로 소수점 에러 ... 이미 인지하고 있었으면서도 순간적으로 깜빡해 실수했다.
무슨 소리냐 하면, 아래와 같은 상황을 가정해보자.

시작점 = (1,2), 타겟점 = (5,4)
탄젠트 법칙에 의거, 쿠션점 = (14/6,0)이다.
그런데 이를 소수로 표현하면 2.333... 과 같이 무한소수가 나온다.
컴퓨터 메모리에는 한계가 있으므로 이 숫자를 완벽히 표현해낼 수 없다.
따라서, 추측하건대 이러한 오차 때문에 위의 풀이가 틀린게 아닐까..
히든 케이스 1~29번이 틀린다.
대칭점 (정답 풀이)
def cushion(m,n,x0,y0,x1,y1,flag):
if flag == 'up':
if y1 >= y0 and x0 == x1:
return INF
return get_dist((x0,2*n-y0),(x1,y1))
if flag == 'down':
if y1 <= y0 and x0 == x1:
return INF
return get_dist((x0,-y0),(x1,y1))
if flag == 'left':
if x1 <= x0 and y0 == y1:
return INF
return get_dist((-x0,y0),(x1,y1))
if flag == 'right':
if x1 >= x0 and y0 == y1:
return INF
return get_dist((2*m-x0,y0),(x1,y1))소수 표현식을 제거하는 방법을 골똘히 생각하다 직선으로 한 번에 가면 되겠다고 떠올렸다.
예를 들어, 아래 그림을 보자.
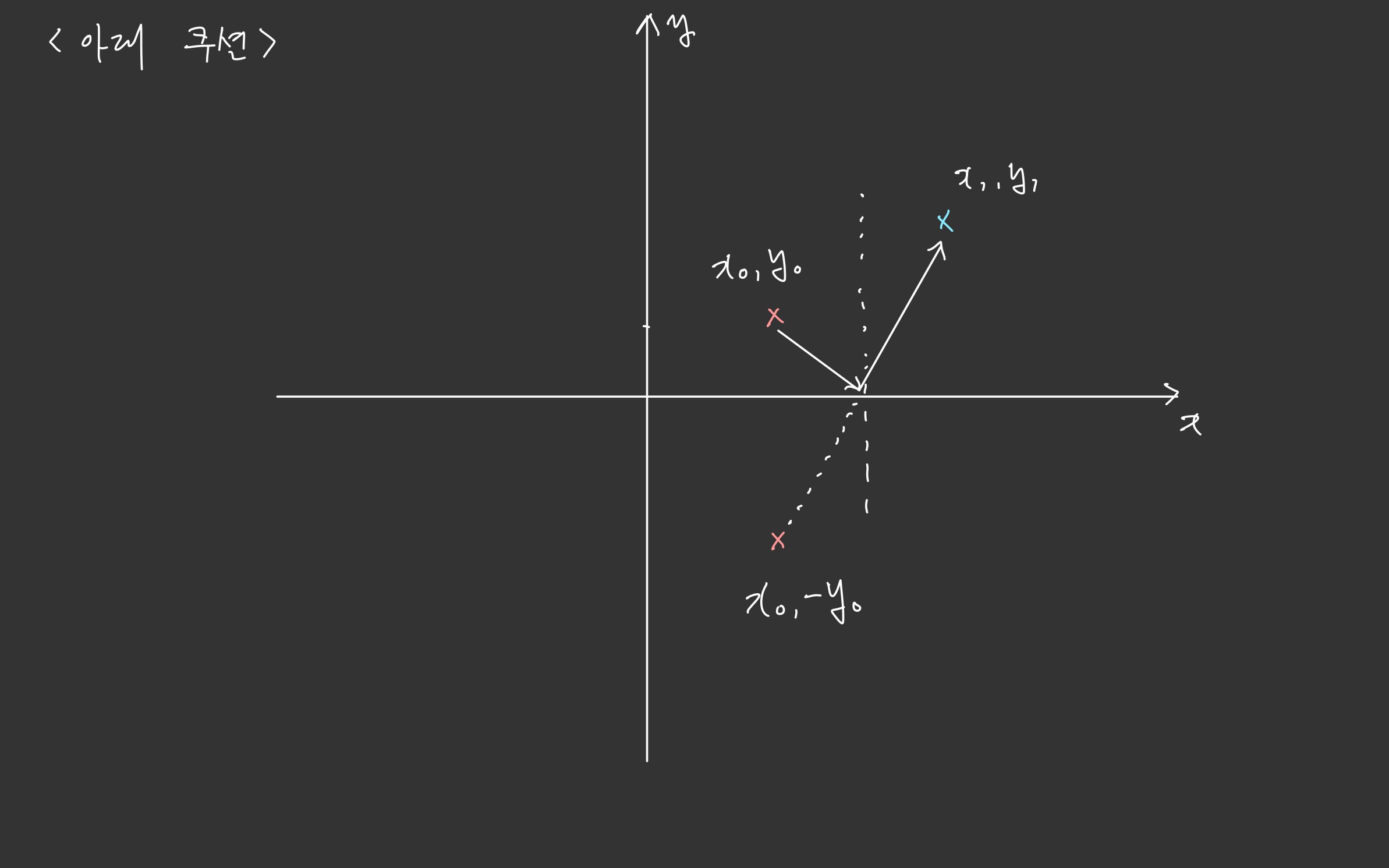
빨간점에서 하단 쿠션을 맞춰 파란점으로 간다고 했을 때, x축 기준으로 대칭시켜 직선 거리를 구하면 그게 곧 원쿠션 거리다.
문제 조건에 따라, 가는 경로에 공이 있는 경우를 제외시켜줬다.
전체 코드
INF = int(1e9)
def get_dist(p0,p1):
return abs(p0[0]-p1[0])**2+abs(p0[1]-p1[1])**2
def cushion(m,n,x0,y0,x1,y1,flag):
if flag == 'up':
if y1 >= y0 and x0 == x1:
return INF
return get_dist((x0,2*n-y0),(x1,y1))
if flag == 'down':
if y1 <= y0 and x0 == x1:
return INF
return get_dist((x0,-y0),(x1,y1))
if flag == 'left':
if x1 <= x0 and y0 == y1:
return INF
return get_dist((-x0,y0),(x1,y1))
if flag == 'right':
if x1 >= x0 and y0 == y1:
return INF
return get_dist((2*m-x0,y0),(x1,y1))
def solution(m, n, startX, startY, ball):
answer = []
flag = ['up','down','left','right']
for i in range(len(ball)):
tmp = INF
for f in flag:
tmp = min(tmp,cushion(m,n,startX,startY,ball[i][0],ball[i][1],f))
answer.append(tmp)
return answer