[KT AIVLE 4기] 머신러닝1

머신러닝은 크게 학습에 따라 세 분류로 나뉜다.

지도학습

학습 대상이 되는 데이터에 정답을 주어 규칙성, 즉 데이터의 패턴을 배우게 하는 학습 방법

• 분류(Classification) - 범줏값을 예측
  • 이미 적절히 분류된 데이터를 학습하여 분류 규칙을 찾고, 그 규칙을 기반으로 새롭게 주어진 데이터를 적절히 분류하는 것을 목적으로 함
• 회귀(Regression) - 연속적인 숫자를 예측
  • 이미 결과값이 있는 데이터를 학습하여 입력 값과 결과 값의 연관성을 찾고, 그 연관성을 기반으로 새롭게 주어진 데이터에 대한 값을 예측하는 것을 목적으로 함

• 분류와 회귀는 서로 다른 함수를 사용해 모델링을 하게 됨

분류 문제	회귀 문제
DecisionTreeClassifier	LinearRegression
KNeighborsClassifier	KNeighborsRegressor
LogisticRegression	DecisionTreeRegressor
RandomForestClassifier	RandomForestRegressor
XGBClassifier	XGBRegressor
---	---
accuracy_score	mean_absolute_error
recall_score	mean_squared_error
precision_score	root mean_squared_error
classification_report	mean_absolute_percentage_error
confusion_matrix	r2_score

비지도학습

정답이 없는 데이터 만으로 배우게 하는 학습 방법

• 군집화(Clustering)
  • 주어진 데이터를 학습하여 적절한 분류 규칙을 찾아 데이터를 분류함을 목적으로 함. 정답이 없으니 성능을 평가하기도 어려움
• 변환(Transform)
• 연관(Association)

강화학습

선택한 결과에 대해 보상을 받아 행동을 개선하면서 배우게 하는 학습 방법

---

📌 회귀 모델 성능 평가

✔️ 회귀 평가 지표 정리

• MSE, Mean Squared Error
  오차 제곱(SSE)의 합을 구한 후 평균을 구함
  $MSE = \displaystyle {\sum{(y-\hat{y})^2} \over n}$

• RMSE, Root Mean Squared Error
  오차의 제곱이므로 루트를 사용해 일반적인 값으로 표현
  $RMSE = \displaystyle \sqrt{\sum{(y-\hat{y})^2} \over n}$

• MAE, Mean Absolute Error
  오차 절댓값의 합을 구한 후 평균을 구함
  $MAE = \displaystyle {\sum\vert{(y-\hat{y})^2\vert} \over n}$
  

• MAPE, Mean Absolute Percentage Error
  오차 비율을 표시하고 싶은 경우 MAPE를 사용함
  $MAPE = \displaystyle {{\sum{\vert{y-\hat{y}\over n}\vert} }\over n}$

✔️ 오차를 보는 다양한 관점

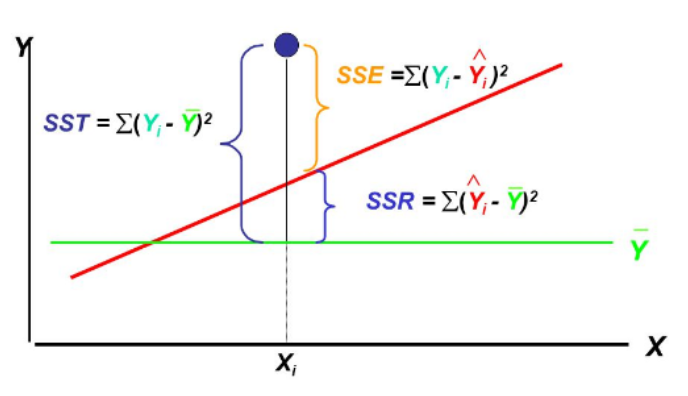
• SST, Sum Squared Total
  전체 오차(최소한 평균 보다는 성능이 좋아야 하니, 우리에게 허용된 오차)
  $SST = \displaystyle {\sum_{i=1}^{n}{(y_i-\bar{y})^2}}$
  
• SSR, Sum squared Regression
  전체 오차 중에서 회귀식이 잡아낸 오차
  $SSR = \displaystyle {\sum_{i=1}^{n}{(\hat{y_i}-\bar{y})^2}}$
  
• SSE, Sum Squared Error
  전체 오차 중에서 회귀식이 여전히 잡아내지 못한 오차
  $SSE = \displaystyle {\sum_{i=1}^{n}{(y_i-\hat{y_i})^2}}$
  $SST=SSR+SSE$

✔️ 결정계수 $R^2$ (R-Squared)

$R^2 = {{SSR} \over {SST}} = 1 - {SSE \over SST}$

• 모델 성능을 해석하기 위해서 만든 MSE의 표준화된 버전이 결정 계수임
• 전체 오차 중에서 회귀식이 잡아낸 오차 비율(일반적으로 0~1 사이)
• 오차의 비 또는 설명력이라고 부름
• $𝑅^2 = 1$이면 $𝑀𝑆𝐸 = 0$이고 모델이 데이터를 완벽하게 학습한 것

---

📌 분류 모델 성능 평가

✔️ 혼동행렬과 평가지표

• Confusion Matrix(오분류표)
  사진출처
  

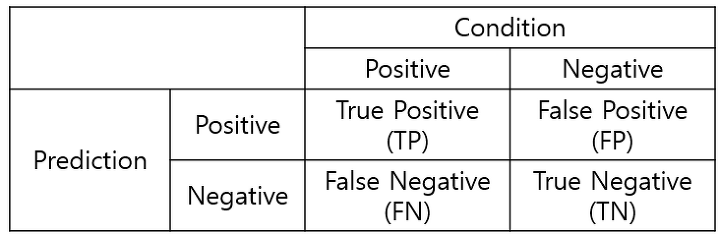
• TN(True Negative, 진음성)
  음성으로 잘 예측한 것(음성을 음성이라고 예측한 것)

• FP(False Positive, 위양성)
  양성으로 잘 못 예측한 것(음성을 양성이라고 예측한 것)

• FN(False Negative, 위음성)
  음성으로 잘 못 예측한 것(양성을 음성이라고 예측한 것)

• TP(True Positive, 진양성)
  양성으로 잘 예측한 것(양성을 양성이라고 예측한 것)

• 정확도(Accuracy)

  $(Accuracy) = \displaystyle {{TN + TP}\over{TN + FP + FN + TP}}$
  • 전체 중에서 Positive와 Negative 로 정확히 예측한(TN + TP) 비율
  • 가장 직관적으로 모델 성능을 확인할 수 있는 평가지표

• 정밀도(Precision)

  $(Precision) = \displaystyle {{TP}\over{FP +TP}}$
  • Positive로 예측한 것(FP + TP) 중에서 실제 Positive(TP)인 비율

• 재현율(Recall)

  $(Recall) = \displaystyle {{TP}\over{FN +TP}}$
  • 실제 Positive(FN + TP) 중에서 Positive로 예측한(TP) 비율
  • 민감도(Sensitivity)라고 부르는 경우가 많음

• 특이도(Specificity)

  $(Specificity) = \displaystyle {{TN}\over{TN +FP}}$
  • 실제 Negative(TN + FP) 중에서 Negative로 예측한(TN) 비율

• F1-Score

  $(F1-Score) = \displaystyle {{2 \times {Precision} \times {Recall}}\over{{Precision} + {Recall}}}$
  • 정밀도와 재현율의 조화 평균
  • 분자가 같지만 분모가 다를 경우, 즉 관점이 다른 경우 조화 평균이 큰 의미를 가짐