블룸 필터 적용후에 언제까지 블룸 필터만 쓸 것인가: Ribbon Filter라는 글을 접하게 되었다.(뜨금)
리본 필터의 데이터 구조는 선형적인 메모리 접근을 가능하게 하여, CPU 캐시 미스를 줄이는데 도움이 될 있다는 내용이 포함되어있었는데...
CPU 캐시 계층 구조에 대해 자세히 알아보고, 테스트 코드로 실제 성능 차이를 측정해보자!
CPU 캐시 계층 구조
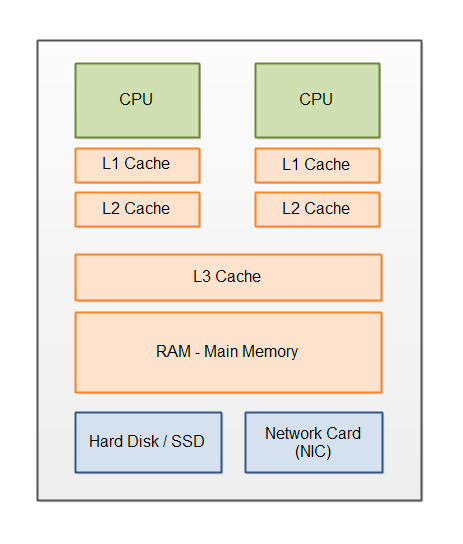
L1 캐시 (Level 1 Cache)
- CPU 코어에 가장 가까이 위치한 최상위 캐시
- 일반적으로 32KB ~ 64KB 크기
- 접근 속도: 약 4 CPU 사이클
- 특징: 명령어 캐시(L1I)와 데이터 캐시(L1D)로 분리되어 있음
L2 캐시 (Level 2 Cache)
- L1 캐시 다음 계층에 위치
- 일반적으로 256KB ~ 512KB 크기
- 접근 속도: 약 10 CPU 사이클
- 특징: 명령어와 데이터를 통합 관리
L3 캐시 (Level 3 Cache)
- 마지막 레벨 캐시 (LLC: Last Level Cache)
- 일반적으로 수 MB ~ 수십 MB 크기
- 접근 속도: 약 40~75 CPU 사이클
- 특징: 여러 코어가 공유하는 통합 캐시
메인 메모리 (Main Memory)
- CPU 캐시 다음 계층에 위치한 주 기억장치
- 일반적으로 수 GB ~ 수백 GB 크기
- 접근 속도: 약 200~300 CPU 사이클
- 특징
- DRAM으로 구성
- 페이지 단위로 관리 (보통 4KB)
- 가상 메모리 시스템을 통해 접근
- 캐시 라인 단위(64바이트)로 CPU 캐시와 데이터 교환
메인 메모리 성능 특성
- 지역성 (Locality)
- 시간적 지역성: 최근 접근한 메모리는 곧 다시 접근될 가능성이 높음
- 공간적 지역성: 접근한 메모리 주변은 곧 접근될 가능성이 높음
- 메모리 계층 간 데이터 이동
- CPU → L1 캐시: 4-5 사이클
- L1 → L2 캐시: 10-12 사이클
- L2 → L3 캐시: 30-40 사이클
- L3 → 메인 메모리: 200-300 사이클
- 메모리 대역폭
- 순차적 접근: 최대 대역폭 활용 가능
- 랜덤 접근: 대역폭 활용도 낮음
- 캐시 라인 크기만큼 한 번에 전송
메모리 접근 패턴이 성능에 미치는 영향
메모리 접근 패턴은 애플리케이션의 성능에 큰 영향을 미친다.
- 순차적 접근의 장점
- 하드웨어 프리페처 효율적 활용
- 메모리 대역폭 최대 활용
- 캐시 라인 활용도 극대화
- TLB(Translation Lookaside Buffer) 히트율 향상
- 랜덤 접근의 단점
- 캐시 미스 증가
- 메모리 레이턴시 증가
- 대역폭 활용도 저하
- 페이지 폴트 가능성 증가
- 캐시 활용도 향상을 위한 고려사항
- 캐시 라인 크기에 맞춘 데이터 구조 설계
- 메모리 정렬(alignment) 고려
- 캐시 오염(pollution) 최소화
- 거짓 공유(false sharing) 방지
MESI 프로토콜
멀티코어 시스템에서 캐시 일관성을 유지하는 핵심 메커니즘이다. 프로세서 간의 캐시 동기화에 사용된다.
캐시 라인의 4가지 상태
-
Modified (수정됨)
- 해당 캐시만이 유효한 데이터를 가지고 있음
- 메인 메모리의 데이터는 오래된 상태
- 다른 프로세서가 이 데이터를 읽으려면 현재 캐시에서 제공해야 함
-
Exclusive (독점)
- 이 캐시만이 유효한 데이터를 가지고 있음
- 메인 메모리의 데이터와 동일한 상태
- 쓰기 발생 시 Modified 상태로 전환 가능
-
Shared (공유)
- 여러 캐시가 동일한 데이터의 복사본을 가지고 있음
- 메인 메모리의 데이터와 동일한 상태
- 읽기만 가능한 상태
-
Invalid (무효)
- 캐시 라인의 데이터가 유효하지 않음
- 다른 프로세서가 데이터를 수정했을 수 있음
- 데이터 접근 시 메인 메모리나 다른 캐시에서 가져와야 함
프로토콜 동작 과정
- Read Hit (읽기 히트)
- Shared/Exclusive/Modified 상태에서 바로 읽기 가능
- 상태 변화 없음
상황: 프로세서가 자신의 캐시에 있는 데이터를 읽으려 할 때
Core1 캐시: Modified (값: 100) 일 때
Core1이 해당 값을 읽으려 하면
- 캐시에서 바로 100을 읽음
- 상태는 Modified 유지
- 버스 트래픽 발생하지 않음- Read Miss (읽기 미스)
- Invalid 상태에서 발생
- 다른 캐시나 메모리에서 데이터 가져옴
- 상태는 Shared 또는 Exclusive로 변경
상황: 프로세서가 캐시에 없는(Invalid) 데이터를 읽으려 할 때
1) 프로세서가 자신의 캐시가 Invalid 상태임을 확인
2) 버스에 읽기 요청 신호를 브로드캐스트
3) 두 가지 경우 발생:
a) 다른 캐시가 Modified 상태로 가지고 있는 경우:
- 해당 캐시가 데이터를 제공
- 메모리도 갱신
- 양쪽 모두 Shared 상태가 됨
b) 다른 캐시가 가지고 있지 않은 경우:
- 메모리에서 데이터 읽어옴
- 상태는 Exclusive가 됨- Write Hit (쓰기 히트)
- Modified/Exclusive 상태에서 바로 쓰기 가능
- Shared 상태면 다른 캐시를 Invalid로 만든 후 Modified로 변경
상황: 프로세서가 자신의 캐시에 있는 데이터를 수정하려 할 때
경우 1) Modified/Exclusive 상태인 경우:
- 바로 쓰기 가능
- Modified 상태로 변경/유지
- 버스 트래픽 없음
경우 2) Shared 상태인 경우:
1) 버스에 Invalid 신호 브로드캐스트
2) 다른 캐시들이 해당 라인을 Invalid로 변경
3) 자신의 캐시를 Modified로 변경
4) 데이터 수정- Write Miss (쓰기 미스)
- Invalid 상태에서 발생
- 데이터를 가져온 후 다른 캐시를 Invalid로 만들고 Modified로 변경
상황: 프로세서가 캐시에 없는(Invalid) 데이터를 수정하려 할 때
1) 버스에 Read-With-Intent-To-Modify 신호 브로드캐스트
2) 데이터 소스 확인:
a) 다른 캐시가 Modified 상태로 가지고 있는 경우:
- 해당 캐시가 데이터 제공
- 메모리도 갱신
b) 다른 캐시가 없는 경우:
- 메모리에서 데이터 읽어옴
3) 다른 모든 캐시의 해당 라인을 Invalid로 변경
4) 자신의 캐시를 Modified로 변경
5) 데이터 수정Java로 캐시 성능 테스트하기
이제 실제로 Java 코드를 통해 캐시 계층 구조가 성능에 미치는 영향을 측정해보자.
테스트 코드
public class CacheLevelTest {
private static final int ARRAY_SIZE = 64 * 1024 * 1024; // 64MB 배열
private static final int[] STRIDE_SIZES = {1, 2, 4, 8, 16, 32, 64};
public static void main(String[] args) {
// 테스트할 배열 생성
int[] array = new int[ARRAY_SIZE];
// 배열 초기화
for (int i = 0; i < ARRAY_SIZE; i++) {
array[i] = i;
}
// 순차 접근 테스트
System.out.println("=== 순차 접근 테스트 ===");
testSequentialAccess(array);
// 랜덤 접근 테스트
System.out.println("\n=== 랜덤 접근 테스트 ===");
testRandomAccess(array);
// 스트라이드 접근 테스트
System.out.println("\n=== 스트라이드 접근 테스트 ===");
testStrideAccess(array);
}
private static void testSequentialAccess(int[] array) {
long startTime = System.nanoTime();
int sum = 0;
for (int i = 0; i < array.length; i++) {
sum += array[i];
}
long endTime = System.nanoTime();
System.out.printf("순차 접근 시간: %.2f ms%n", (endTime - startTime) / 1_000_000.0);
}
private static void testRandomAccess(int[] array) {
long startTime = System.nanoTime();
int sum = 0;
for (int i = 0; i < array.length; i++) {
int randomIndex = (int) (Math.random() * array.length);
sum += array[randomIndex];
}
long endTime = System.nanoTime();
System.out.printf("랜덤 접근 시간: %.2f ms%n", (endTime - startTime) / 1_000_000.0);
}
private static void testStrideAccess(int[] array) {
for (int stride : STRIDE_SIZES) {
long startTime = System.nanoTime();
int iterations = array.length / stride; // 실제 접근 횟수 계산
int sum = 0;
for (int i = 0; i < array.length; i += stride) {
sum += array[i];
}
long endTime = System.nanoTime();
double timePerAccess = (endTime - startTime) / (double)iterations; // 접근당 평균 시간 계산
System.out.printf("스트라이드 %d 접근당 평균 시간: %.2f ns%n",
stride, timePerAccess);
}
}=== 순차 접근 테스트 ===
순차 접근 시간: 24.89 ms
=== 랜덤 접근 테스트 ===
랜덤 접근 시간: 9753.09 ms
=== 스트라이드 접근 테스트 ===
스트라이드 1 접근당 평균 시간: 0.58 ns
스트라이드 2 접근당 평균 시간: 0.74 ns
스트라이드 4 접근당 평균 시간: 0.65 ns
스트라이드 8 접근당 평균 시간: 0.65 ns
스트라이드 16 접근당 평균 시간: 1.19 ns
스트라이드 32 접근당 평균 시간: 3.88 ns
스트라이드 64 접근당 평균 시간: 4.90 ns테스트 결과 분석
실제 테스트를 실행해보면 다음과 같은 패턴을 관찰할 수 있다.
-
순차 접근 성능
- 가장 빠른 접근 속도 기록
- 캐시 라인을 최대한 활용하는 패턴
-
랜덤 접근 성능
- 가장 느린 접근 속도
- 캐시 미스가 빈번하게 발생
- 메인 메모리 접근이 자주 발생
-
스트라이드 접근 성능
- 스트라이드 크기가 커질수록 성능 저하
- 캐시 라인 활용도가 감소
성능 최적화 팁
테스트 결과를 바탕으로, 다음과 같은 최적화 전략을 적용할 수 있다.
- 데이터 지역성 활용
- 시간 지역성: 최근 접근한 데이터를 재사용
- 공간 지역성: 연속된 메모리 위치의 데이터 활용
- 캐시 친화적 데이터 구조
- 배열과 같은 연속된 메모리 구조 활용
- LinkedList 보다 ArrayList 선호
- 메모리 접근 패턴 최적화
- 순차적 접근 패턴 활용
- 랜덤 접근 최소화
- 적절한 데이터 청크 크기 설정
결론
- 대용량 데이터를 처리하는 애플리케이션의 경우, 캐시 친화적인 알고리즘과 데이터 구조를 선택하는 것이 중요하다.

안녕하세요, 선생님. 블로그 글 잘 보고 있습니다.
혹시 선생님 멘토링 같은 건 안 하시나요?