BOJ 1004 (어린 왕자)

• 문제
  어린 왕자는 소혹성 B-664에서 자신이 사랑하는 한 송이 장미를 위해 살아간다. 어느 날 장미가 위험에 빠지게 된 것을 알게 된 어린 왕자는, 장미를 구하기 위해 은하수를 따라 긴 여행을 하기 시작했다. 하지만 어린 왕자의 우주선은 그렇게 좋지 않아서 행성계 간의 이동을 최대한 피해서 여행해야 한다. 아래의 그림은 어린 왕자가 펼쳐본 은하수 지도의 일부이다.
  
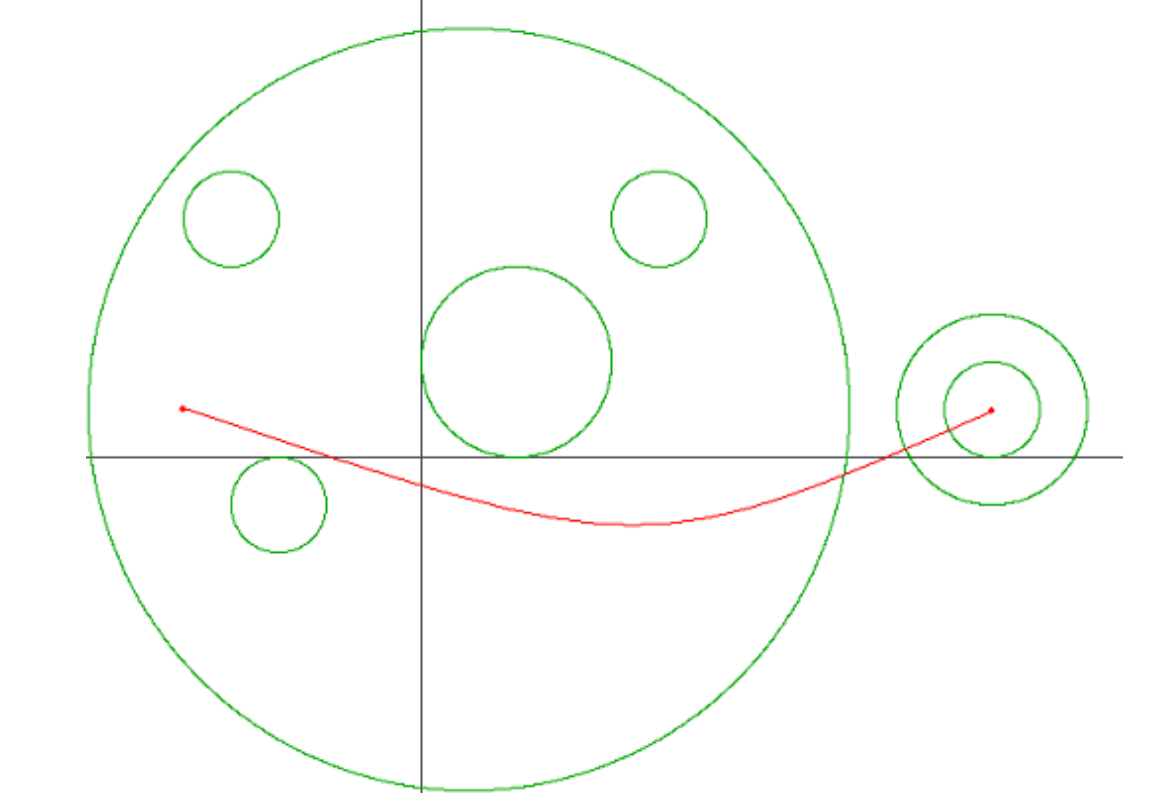
  빨간 실선은 어린 왕자가 출발점에서 도착점까지 도달하는데 있어서 필요한 행성계 진입/이탈 횟수를 최소화하는 경로이며, 원은 행성계의 경계를 의미한다. 이러한 경로는 여러 개 존재할 수 있지만 적어도 3번의 행성계 진입/이탈이 필요하다는 것을 알 수 있다.
  
  위와 같은 은하수 지도, 출발점, 도착점이 주어졌을 때 어린 왕자에게 필요한 최소의 행성계 진입/이탈 횟수를 구하는 프로그램을 작성해 보자. 행성계의 경계가 맞닿거나 서로 교차하는 경우는 없다. 또한, 출발점이나 도착점이 행성계 경계에 걸쳐진 경우 역시 입력으로 주어지지 않는다.
  
  
• 입력
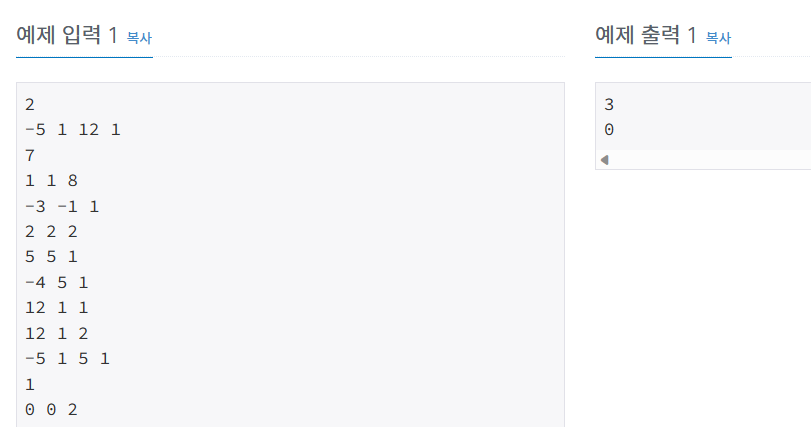
  입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 첫째 줄에 출발점 (x1, y1)과 도착점 (x2, y2)이 주어진다. 두 번째 줄에는 행성계의 개수 n이 주어지며, 세 번째 줄부터 n줄에 걸쳐 행성계의 중점과 반지름 (cx, cy, r)이 주어진다.
  
  
• 출력
  각 테스트 케이스에 대해 어린 왕자가 거쳐야 할 최소의 행성계 진입/이탈 횟수를 출력한다.
  
  
• 제한
  - 1000 ≤ x1, y1, x2, y2, cx, cy ≤ 1000
  - 1 ≤ r ≤ 1000
  - 1 ≤ n ≤ 50
  - 좌표와 반지름은 모두 정수

#include<iostream>
#include<cmath>
using namespace std;
int testCount, planetCount;
pair<int, int> departure;
pair<int, int> destination;
bool departureFlag, destinationFlag;
int answer;

void fast_io() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);
}

void input() {
	cin >> testCount;
}

void solve() {
	while (testCount--) {
		cin >> departure.first >> departure.second
			>> destination.first >> destination.second;
		cin >> planetCount;
		for (int i = 1; i <= planetCount; i++) {
			int centerX, centerY, radius;
			cin >> centerX >> centerY >> radius;
			if (pow(departure.first - centerX, 2) + pow(departure.second - centerY, 2) < radius * radius)
				departureFlag = true;
			if (pow(destination.first - centerX, 2) + pow(destination.second - centerY, 2) < radius * radius)
				destinationFlag = true;
			if (departureFlag != destinationFlag)
				answer++;
			departureFlag = false; destinationFlag = false;
		}
		cout << answer << '\n';
		answer = 0;
	}
}

int main() {
	fast_io();
	input();
	solve();
	return 0;
}

   1002번 터렛과 유사한 문제로 원의 중심과 반지름을 이용하여 푸는 문제이다.
고려해야할 경우의 수는

1. 시작점과 도착점 모두 원 내부에 있는 경우
2. 시작점과 도착점 모두 원 바깥에 있는 경우
3. 시작점 또는 도착점 둘 중 하나만 원 안에 있는 경우

이렇게 3가지가 있다

1번과 2번 경우는 뽑아놓고 알아서 고른다는 조합의 느낌처럼 위의 그림과 같이 곡선 형태로 알아서 피해갈 것이다

3번 경우는 반드시 점을 통과하거나 탈출하게 되므로 이때 횟수를 1회 늘려주면 된다.
(각 점별 boolean 값인 Flag를 두어 영역 내부에 포함된 여부를 확인하도록 하였다)

위의 코드에서 TestCase 입력 때문에 input() 함수에 testCount만 입력받도록 했는데 분리해서 짜면 더 깔끔해질 것 같다.

시간 복잡도 : O(N)

숏코딩

#include <bits/stdc++.h>
using namespace std;
void f(){
	int n,a,b,c,d,cnt=0;
	cin>>a>>b>>c>>d>>n;
	while(n--){
		int x,y,z;
		cin>>x>>y>>z;
		cnt+=((x-a)*(x-a)+(y-b)*(y-b)<z*z)^((x-c)*(x-c)+(y-d)*(y-d)<z*z);
	}
	cout<<cnt<<'\n';
}
int main(){
	int n;
	cin>>n;
	while(n--)
		f();
}

그냥 ^ 연산자로 한방에 해결해버린 것 같다...