BOJ 1932 (정수 삼각형)

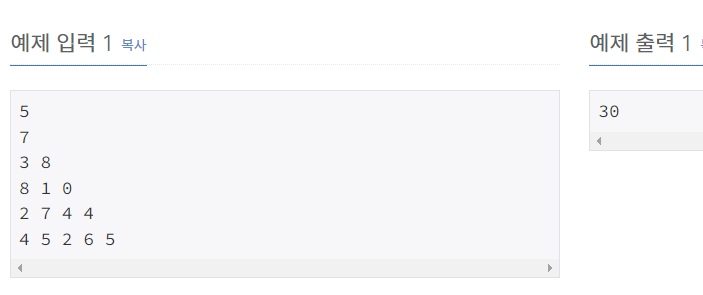
• 문제
  7
  3 8
  8 1 0
  2 7 4 4
  4 5 2 6 5
  위 그림은 크기가 5인 정수 삼각형의 한 모습이다.
  맨 위층 7부터 시작해서 아래에 있는 수 중 하나를 선택하여 아래층으로 내려올 때, 이제까지 선택된 수의 합이 최대가 되는 경로를 구하는 프로그램을 작성하라.
  
  아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다.
  
  삼각형의 크기는 1 이상 500 이하이다. 삼각형을 이루고 있는 각 수는 모두 정수이며, 범위는 0 이상 9999 이하이다.
  
  
• 입력
  첫째 줄에 삼각형의 크기 n(1 ≤ n ≤ 500)이 주어지고, 둘째 줄부터 n+1번째 줄까지 정수 삼각형이 주어진다.
  
  
• 출력
  첫째 줄에 합이 최대가 되는 경로에 있는 수의 합을 출력한다.

#include<iostream>
using namespace std;
int N;
int tri[501][501];

void fast_io()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);
}

int main()
{
	fast_io();
	cin >> N;
	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j <= i; j++)
		{
			int num; cin >> num;
			tri[i][j] = num;
		}
	}

	for (int i = N - 1; i > 0; i--)
	{
		for (int j = 0; j < i; j++)
		{
			tri[i - 1][j] += max(tri[i][j], tri[i][j + 1]);
		}
	}
	cout << tri[0][0];
	return 0;
}

  Dynamic Programming 기법을 쓰는 문제이다. 위에서 부터 아래로 가며 더해가는 방법으로 풀었으나 다른 분이 작성한 코드를 참고했는데 아래서 위로 더해주면 코드가 정말 짧아진다.

시간 복잡도 : O(N^2)