BOJ 2477 (참외밭)

• 문제
  시골에 있는 태양이의 삼촌 댁에는 커다란 참외밭이 있다. 문득 태양이는 이 밭에서 자라는 참외가 도대체 몇 개나 되는지 궁금해졌다. 어떻게 알아낼 수 있는지 골똘히 생각하다가 드디어 좋은 아이디어가 떠올랐다.
  유레카! 1m2의 넓이에 자라는 참외 개수를 헤아린 다음, 참외밭의 넓이를 구하면 비례식을 이용하여 참외의 총개수를 구할 수 있다.
  
  1m2의 넓이에 자라는 참외의 개수는 헤아렸고, 이제 참외밭의 넓이만 구하면 된다. 참외밭은 ㄱ-자 모양이거나 ㄱ-자를 90도, 180도, 270도 회전한 모양(┏, ┗, ┛ 모양)의 육각형이다. 다행히도 밭의 경계(육각형의 변)는 모두 동서 방향이거나 남북 방향이었다.
  밭의 한 모퉁이에서 출발하여 밭의 둘레를 돌면서 밭경계 길이를 모두 측정하였다.
  
  
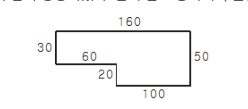
  예를 들어 참외밭이 위 그림과 같은 모양이라고 하자. 그림에서 오른쪽은 동쪽, 왼쪽은 서쪽, 아래쪽은 남쪽, 위쪽은 북쪽이다. 이 그림의 왼쪽위 꼭짓점에서 출발하여, 반시계방향으로 남쪽으로 30m, 동쪽으로 60m, 남쪽으로 20m, 동쪽으로 100m, 북쪽으로 50m, 서쪽으로 160m 이동하면 다시 출발점으로 되돌아가게 된다.
  
  위 그림의 참외밭 면적은 6800m2이다. 만약 1m2의 넓이에 자라는 참외의 개수가 7이라면, 이 밭에서 자라는 참외의 개수는 47600으로 계산된다.
  
  1m^2의 넓이에 자라는 참외의 개수와, 참외밭을 이루는 육각형의 임의의 한 꼭짓점에서 출발하여 반시계방향으로 둘레를 돌면서 지나는 변의 방향과 길이가 순서대로 주어진다. 이 참외밭에서 자라는 참외의 수를 구하는 프로그램을 작성하시오.
  
  
• 입력
  첫 번째 줄에 1m2의 넓이에 자라는 참외의 개수를 나타내는 양의 정수 K (1 ≤ K ≤ 20)가 주어진다. 참외밭을 나타내는 육각형의 임의의 한 꼭짓점에서 출발하여 반시계방향으로 둘레를 돌면서 지나는 변의 방향과 길이 (1 이상 500 이하의 정수) 가 둘째 줄부터 일곱 번째 줄까지 한 줄에 하나씩 순서대로 주어진다. 변의 방향에서 동쪽은 1, 서쪽은 2, 남쪽은 3, 북쪽은 4로 나타낸다.
  
  
• 출력
  첫째 줄에 입력으로 주어진 밭에서 자라는 참외의 수를 출력한다.

#include<iostream>
#include<vector>
using namespace std;
int K;
vector<pair<int, int>> v;
int check[5];
void fast_io()
{
	ios_base::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);
}

int main()
{
	fast_io();
	int angle = 6; int whole = 1; int small = 1;
	cin >> K;
	while (angle--)
	{
		int dir, length; cin >> dir >> length;
		v.push_back(make_pair(dir, length));
		check[dir]++;
	}
	for (int i = 0; i < 6; i++)
	{
		if (check[v[i].first] == 1)
		{
			whole *= v[i].second;
			continue;
		}
		int next = (i + 1) % 6;
		int d_next = (i + 2) % 6;
		if (v[i].first == v[d_next].first)
		{
			small *= v[next].second;
		}
	}
	cout << (whole - small) * K;
}

  육각형의 모양이 90도로만 회전된 형태로 되어있기 때문에 전체 넓이 - 잘릴 부분의 넓이로 구하고 면적 당 참외 갯수 만큼 곱해주면 되는 문제이다.

잘리는 부분을 파악하는 것이 중요한데 방향이 가로(동,서), 세로(남,북)에서 방향이 1이 나오는 부분이 전체 큰 사각형의 길이이고 가로, 세로에서 두 방향 연달아 나오는 것 사이에 있는 부분이 잘려나갈 부분의 가로, 세로 길이가 된다