문제
최근에 ICPC 탐사대는 남아메리카의 잉카 제국이 놀라운 문명을 지닌 카잉 제국을 토대로 하여 세워졌다는 사실을 발견했다. 카잉 제국의 백성들은 특이한 달력을 사용한 것으로 알려져 있다. 그들은 M과 N보다 작거나 같은 두 개의 자연수 x, y를 가지고 각 년도를 <x:y>와 같은 형식으로 표현하였다. 그들은 이 세상의 시초에 해당하는 첫 번째 해를 <1:1>로 표현하고, 두 번째 해를 <2:2>로 표현하였다. <x:y>의 다음 해를 표현한 것을 <x':y'>이라고 하자. 만일 x < M 이면 x' = x + 1이고, 그렇지 않으면 x' = 1이다. 같은 방식으로 만일 y < N이면 y' = y + 1이고, 그렇지 않으면 y' = 1이다. <M:N>은 그들 달력의 마지막 해로서, 이 해에 세상의 종말이 도래한다는 예언이 전해 온다.
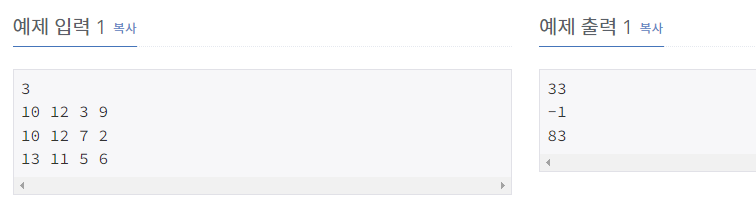
예를 들어, M = 10 이고 N = 12라고 하자. 첫 번째 해는 <1:1>로 표현되고, 11번째 해는 <1:11>로 표현된다. <3:1>은 13번째 해를 나타내고, <10:12>는 마지막인 60번째 해를 나타낸다.
네 개의 정수 M, N, x와 y가 주어질 때, <M:N>이 카잉 달력의 마지막 해라고 하면 <x:y>는 몇 번째 해를 나타내는지 구하는 프로그램을 작성하라.
- 입력
입력 데이터는 표준 입력을 사용한다. 입력은 T개의 테스트 데이터로 구성된다. 입력의 첫 번째 줄에는 입력 데이터의 수를 나타내는 정수 T가 주어진다. 각 테스트 데이터는 한 줄로 구성된다. 각 줄에는 네 개의 정수 M, N, x와 y가 주어진다. (1 ≤ M, N ≤ 40,000, 1 ≤ x ≤ M, 1 ≤ y ≤ N) 여기서 <M:N>은 카잉 달력의 마지막 해를 나타낸다.- 출력
출력은 표준 출력을 사용한다. 각 테스트 데이터에 대해, 정수 k를 한 줄에 출력한다. 여기서 k는 <x:y>가 k번째 해를 나타내는 것을 의미한다. 만일 <x:y>에 의해 표현되는 해가 없다면, 즉, <x:y>가 유효하지 않은 표현이면, -1을 출력한다.
처음 풀이
#include<iostream>
using namespace std;
int M, N, x, y;
void fast_io()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
}
int icpc(int first, int second, int t1, int t2)
{
int temp1 = 1; int temp2 = 1; int count = 1; bool check = true;
while (!(temp1 == t1 && temp2 == t2))
{
if (temp1 < first && temp2 < second)
{
temp1++; temp2++;
count++; continue;
}
else if (temp1 < first && temp2 >= second)
{
temp1++; temp2 = 1;
count++; continue;
}
else if (temp1 >= first && temp2 < second)
{
temp1 = 1; temp2++;
count++; continue;
}
check = false;
break;
}
if (!check)
{
return -1;
}
else return count;
}
int main()
{
void fast_io();
int T; cin >> T;
while (T--)
{
cin >> M >> N >> x >> y;
cout << icpc(M, N, x, y) << '\n';
}
}정말 그대로 반복문을 엄청 돌렸다. 문제 조건에서 범위가 M과 N의 범위가 40000이라 당연히 시간초과가 날 것 같았음 (문제에 주어진 기대입력 기대 출력은 나오기는 함)
최대공약수 최소공배수 이용한 풀이
#include<iostream>
using namespace std;
int M, N, x, y;
void fast_io()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
}
int GCD(int num1, int num2)
{
if (num2 == 0)
{
return num1;
}
return GCD(num2, num1 % num2);
}
int LCM(int num1, int num2)
{
return (num1 * num2) / GCD(num1, num2);
}
int main()
{
void fast_io();
int T; cin >> T;
while (T--)
{
int result = -1;
cin >> M >> N >> x >> y;
int MAX = LCM(M, N);
for (int i = x; i <= MAX; i += M)
{
int temp = i % N;
if (temp == 0) temp = N;
if (temp == y) {
result = i;
break;
}
}
cout << result << '\n';
}
}나머지에서 M만큼 반복될 때마다 원하는 타겟이 나오게 된다. 멸망하는 해는 두 수의 최소 공배수가 되므로 반복문을 돌려주고 나머지 숫자는 타겟 해와 나누었을 때 나머지가 y와 일치할 때 원하는 결과를 얻을 수 있었다.