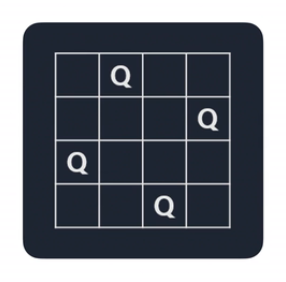
백트래킹
모든 경우의 수를 탐색하는 알고리즘이다.
DFS나 BFS를 활용해서도 백트래킹이 가능하다.
탐색 효율을 위해 굳이 확인하지 않아도 되는 곳을 미리 제거하는 것을 가지치기(Pruning)이라고 부른다.
자바스크립트는 재귀 구조에 대한 효율이 나쁘기 때문에 DFS를 구현할 시 웬만하면 스택을 이용하는 것이 좋다. 그래서 코딩 테스트에서는 이를 위해 보통 재귀로 작성해서 풀 수 있도록 문제를 제출한다고 한다.
따라서 탐색에서 순환(사이클)이 발생할 가능성이 있다면 BFS를 사용하는 것이 편리하다.
BFS와 DFS는 그래프 탐색뿐만 아니라 백트래킹과 같이 효율적인 탐색에도 빈번하게 사용되므로 기본적인 로직과 구현법을 숙지해두자!
백트래킹의 핵심은 가지치기
가지치기를 얼마나 잘하느냐에 따라 백트래킹의 효율성을 좌지우지한다.
How to 백트래킹
- 모든 경우의 수를 찾을 수 있도록 코딩한다.
- 특정한 조건이 만족하는 것만 찾도록 그 이외 필요없는 나머지를 탐색하지 않도록 조건문을 설정한다.
- 절대로 답이 될 수 없는 것은 과감히 제거 및 종료한다.
N-Queen 문제
대표적인 백트래킹에 관한 코딩테스트 문제이다.
길이가 N인 체스판 위에 N개의 퀸이 서로를 공격할 수 없도록 배치할 수 있는 경우의 수를 구하는 문제
문제 해결 방법
백트래킹을 위해서는 모든 경우의 수를 일단 찾아야 한다. (Just do it!)
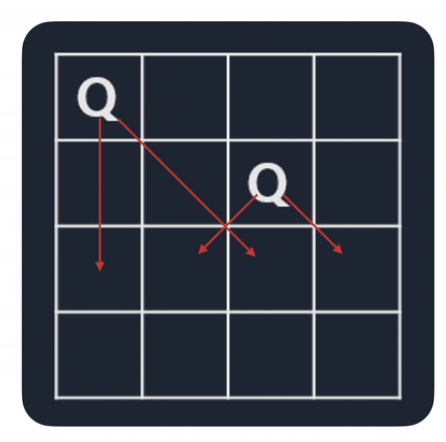
1. (1,1)에 퀸을 배치한다.
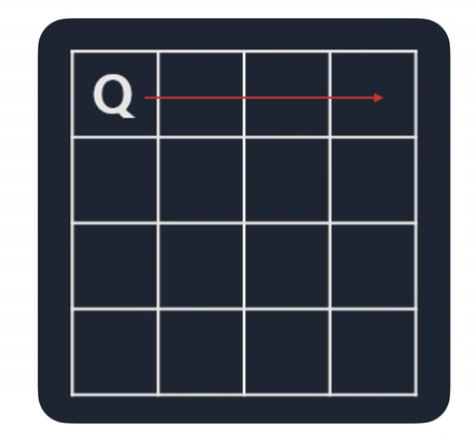
- 첫 줄은 더이상 퀸을 둘 수 없다. 다음 줄로 이동한다.
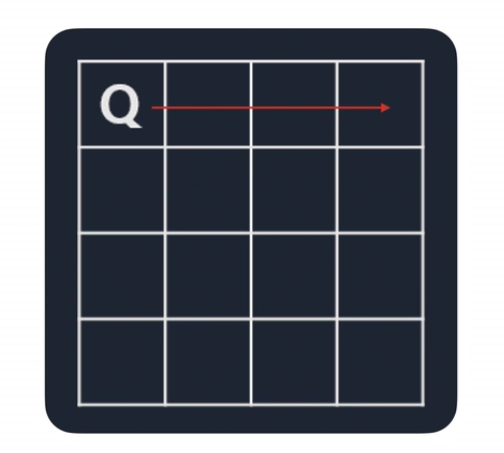
- 바로 아래에도 둘 수 없다.

- 대각선도 둘 수 없다.
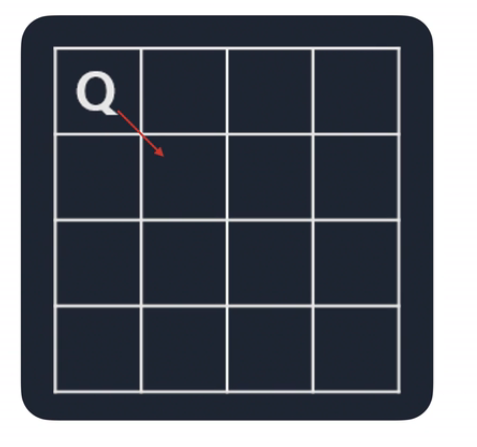
- (2, 3)부터 둘 수 있다.

- 더 이상 퀸을 둘 수 없으므로 탐색을 종료한다.
2. (1, 2)에 퀸을 둔다.
- 과정 1.과 마찬가지로 둘 수 없는 곳을 제외하면서 둔다.
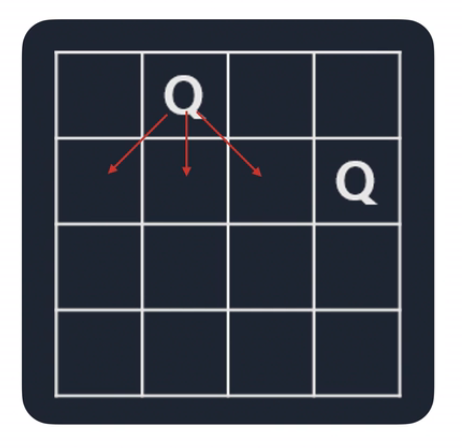
- 결과적으로 N개의 퀸을 둘 수 있는 경우의 수를 찾을 수 있다.
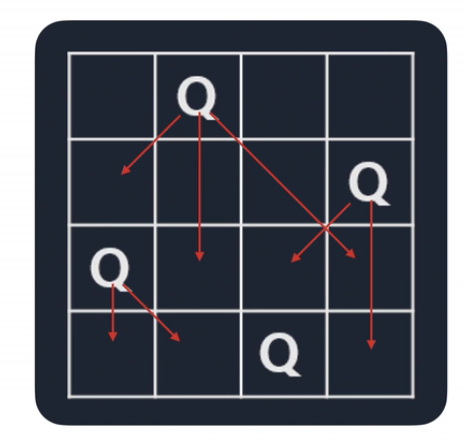
문제 해결 아이디어
1. 2차원배열로 탐색을 하려면 시간이 너무 오래 걸려 비효율적이다. 따라서 한 행에는 퀸이 하나만 놓일 수 있으므로 1차원 배열로arr[row] = col형태로 축약이 가능하다.
2. 대각선에 퀸이 놓여 있는지 체크하기 위해arr[row] = col에서 row 끼리의 차와 col끼리의 차가 같은지 확인하면 된다.
예를 들어 아래 그림과 같이 (0,1)과 (1,2)은 대각선에 놓여 있다. 이 때 행의 0과 1의 차와 열의 1과 2의 차는 1로 같다. 이 점을 착안한 것이다.
// 퀸을 놓을 수 있는지 확인하는 함수
function possible(arr, row) {
// 열은 1차원 배열로 축소했기에 체크 가능
// 행과 대각선만 체크하면 된다.
for (let i=0; i<row; i++) {
// 놓을 수 없으면 false
if (arr[i] === arr[row] || Math.abs(arr[i] - arr[row]) === row - i) return false;
}
return true;
}
// n개의 퀸을 놓을 수 있는 경우의 수 구하는 함수
function nQueen(arr, row, n) {
let count = 0;
if (n === row) {
return 1
}; // 마지막 열까지 체크하고 가능하면 +1
for (let i=0; i<n; i++) {
arr[row] = i; // 퀸을 둔다.
if (possible(arr, row)) { // 이전 퀸 체크 후 가능하면 다음 행 넘어가기
count += nQueen(arr, row+1, n);
}
}
return count;
}
function solution(n) {
let answer = 0;
let chess = Array(n).fill(0);
return answer = nQueen(chess, 0, n);
}😅 해당 내용은 공부하면서 정리한 글입니다. 틀린 부분이나 오해하고 있는 부분이 있다면 피드백 부탁드립니다.