시간복잡도

빅오표기법(Big-O notation)

프로그램의 성능을 대략적으로 파악하기 위한 상대적인 표기법
시간복잡도를 나타내기 위한 방법

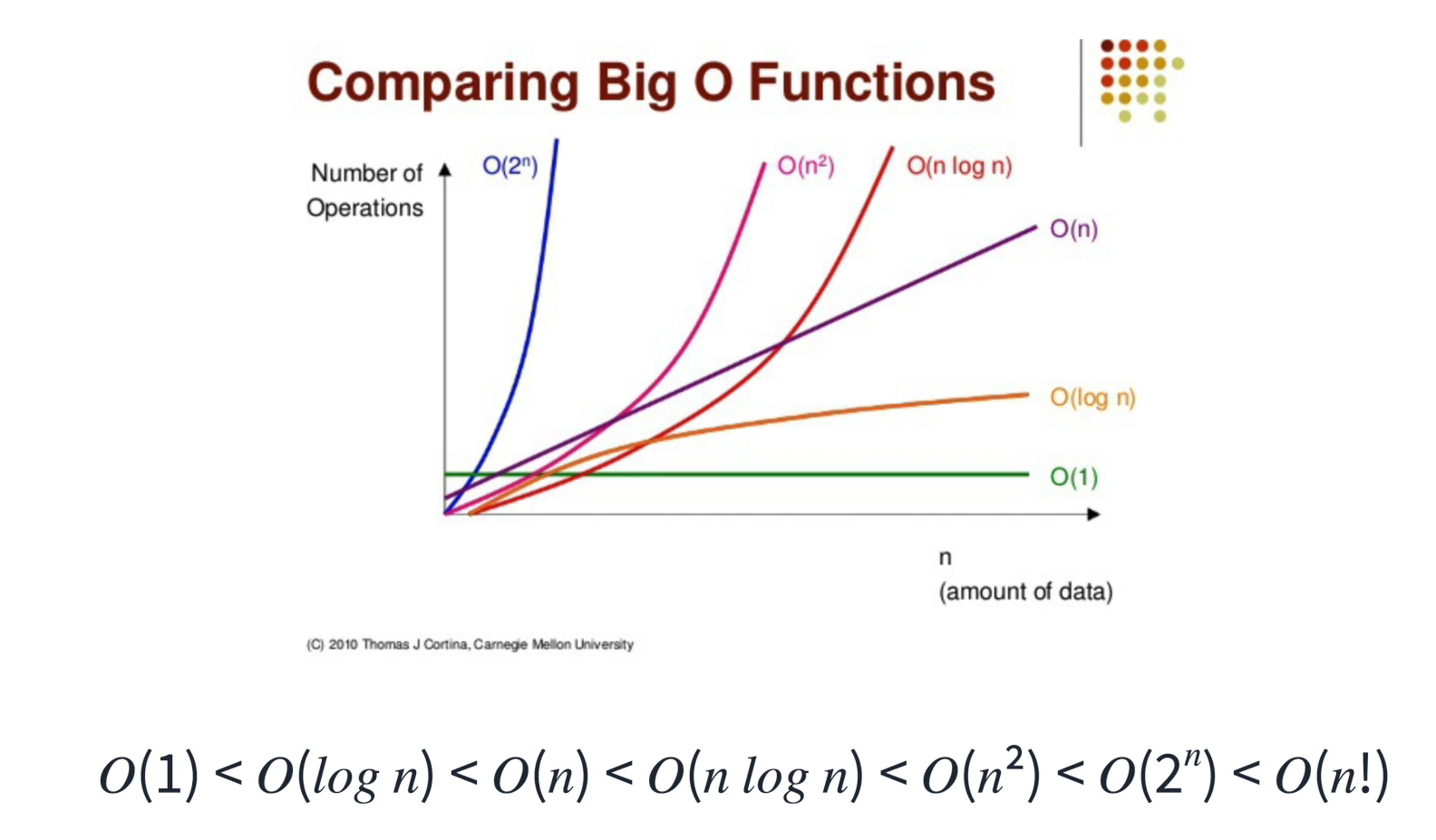
출처: 이선협 강사님 데브코스 강의 자료

O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(2^n) < O(n!)
왼쪽에서 오른쪽으로 갈 수록 성능이 저하된다.
log의 지수는 2이다.

코드로 시간복잡도 알아보기

- O(n)

for (let i=0; i<n; i+=1) {
    // ...
}

- O(log n)

for (let i=1; i<=n; i*=2) {
    // ...
}

- O(n log n)

for (let i = 0; i < n; i += 1) {
  for (let j = 1; j <= n; j *= 2) {
    // ...
  }
}

- O(n^2)

for (let i = 0; i < n; i += 1) {
  for (let j = 0; j < n; j += 1) {
    // ...
  }
}

빅오표기법의 4가지 법칙

계수 법칙

빅오표기법은 점근적 표기법을 따르므로 상수나 계수는 무시한다.
상수 k가 0보다 클 때 f(n) = O(g(n)) 이면 kf(n) = O(g(n))이다.
n이 무한에 가까울 수록 k의 크기는 의미가 없기 때문이다.
실제 성능에는 k 값이 영향을 미칠 수는 있다.

for (let i = 0; i < n; i += 1) {
  // ...
}

// 두 반복문은 모두 O(n)으로 표기된다.

for (let i = 0; i < n * 5; i += 1) {
  // ...
}

합의 법칙

f(n) = O(h(n))이고 g(n) = O(p(n))이면 f(n) + g(n) = O(h(n)) + O(p(n))이다.
빅오는 더해질 수 있다.

for (let i = 0; i < n; i += 1) {
  // ...
}

// 두 반복문을 합치면 O(n + m)으로 표기된다.
// 계수 법칙으로 상수 5는 무시

for (let i = 0; i < m * 5; i += 1) {
  // ...
}

곱의 법칙

f(n) = O(h(n))이고 g(n) = O(p(n))이면 f(n) g(n) = O(h(n)) O(p(n))이다.
빅오는 곱해질 수 있다.

// 두 반복문을 곱하면 O(n^2)으로 표기된다.
// 계수 법칙으로 상수 5는 무시
for (let i = 0; i < n; i += 1) {
  for (let j = 0; j < n * 5; j += 1) {
  	// ...
  }
}

다항 법칙

f(n)이 k차 다항식이면 f(n)은 O(n^k)이다.

// O(n^3)으로 표기된다.
for (let i = 0; i < n * n * n; i += 1) {
  // ...
}

✨ 2가지만 기억하자

1. 상수항은 무시

// 계수 법칙으로 계수(상수)는 무시, O(n + m)으로 표기된다.
for (let i = 0; i < n * 3; i += 1) {
    // ...
}
for (let i = 0; i < m * 2; i += 1) {
    // ...
}

2. 가장 큰 항 외엔 무시

// O(n^2 + n)에서 가장 큰 항만 적용하여 O(n^2)으로 표기
for (let i = 0; i < n; i += 1) {
    // ...
}
for (let i = 0; i < n; i += 1) {
  for (let j = 0; j < n; j += 1) {
    // ...
  }
}

실제 성능 측정 방법

Date 객체를 사용

console.log('시작');
const startTime = new Date().getTime();
const N = 1000000000;

let total = 0;
for (let i = 0; i < N; i++) {
  total += 1;
}
const endTime = new Date().getTime();
console.log(endTime - startTime);
console.log('끝');

0.7초 정도 걸린 것을 확인할 수 있다.