1. 전화번호 - 카운팅 정렬

풀이

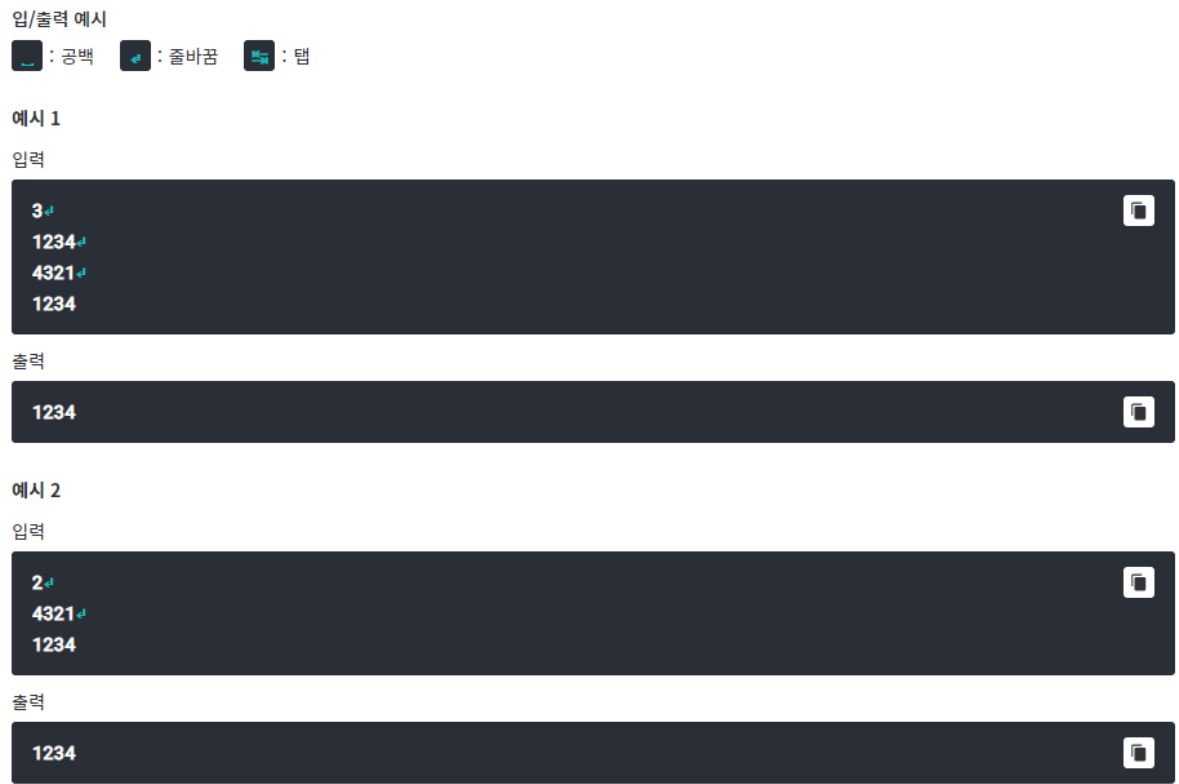
• 이 문제는 전화번호의 범위가 0~9999로 정해져 있으므로 카운팅 정렬을 사용하면 쉽게 해결할 수 있다.
• 이렇게 0~9999까지의 int 배열 table을 0으로 초기화해두고, 입력받은 data값 자체를 table 배열의 인덱스로 사용해 카운트(++)해주면 정렬된 빈도수를 구할 수 있다.
• 그렇게 정렬된 table 배열 전체를 탐색하며, 전화번호 i의 카운트 중 최댓값만 구해주면 된다.

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;

const int MAX_TABLE_LENGH = 10000;//전화번호 4자 최대 크기

//카운팅 정렬 수행 함수
void fillFrequencyTable(vector<int>& data, vector<int>& table) {

    for (int i = 0; i < data.size(); i++) {
        table[data[i]]++;
    }
}

//가장 많이 등장한 번호 반환 함수(여러개인 경우 사전순 빠른것)
int getFreqeuntMember(vector<int> data) {
    
    vector<int> table(MAX_TABLE_LENGH);
        
    //카운팅 정렬 수행
    fillFrequencyTable(data, table);

    int frequentNum = 0;//최대 카운팅 수 저장 변수

    //카운팅 배열(전화번호 i) 전체를 탐색하며
    for (int i = 1; i < table.size(); i++) {

        //빈도수 더 큰 수 등장 시 최댓값을 갱신
        //단, 같은 경우(<=) 갱신x하므로 사전순 빠른것만 담기게 됨
        if (table[frequentNum] < table[i]) {
            frequentNum = i;
        }
    }
    return frequentNum;

}

int main() {

    //전화번호 수 N입력
    int n;
    cin >> n;

    //N개의 전화번호 뒷자리 4자 입력(0000~9999)
    vector<int> data(n);
    for (int i = 0; i < n; i++) {
        cin >> data[i];
    }

    //빈도수 가장 높은 전화번호 반환
    int result = getFreqeuntMember(data);

    //결과 출력
    cout << result << endl;

    return 0;
}

2. 페인트

풀이

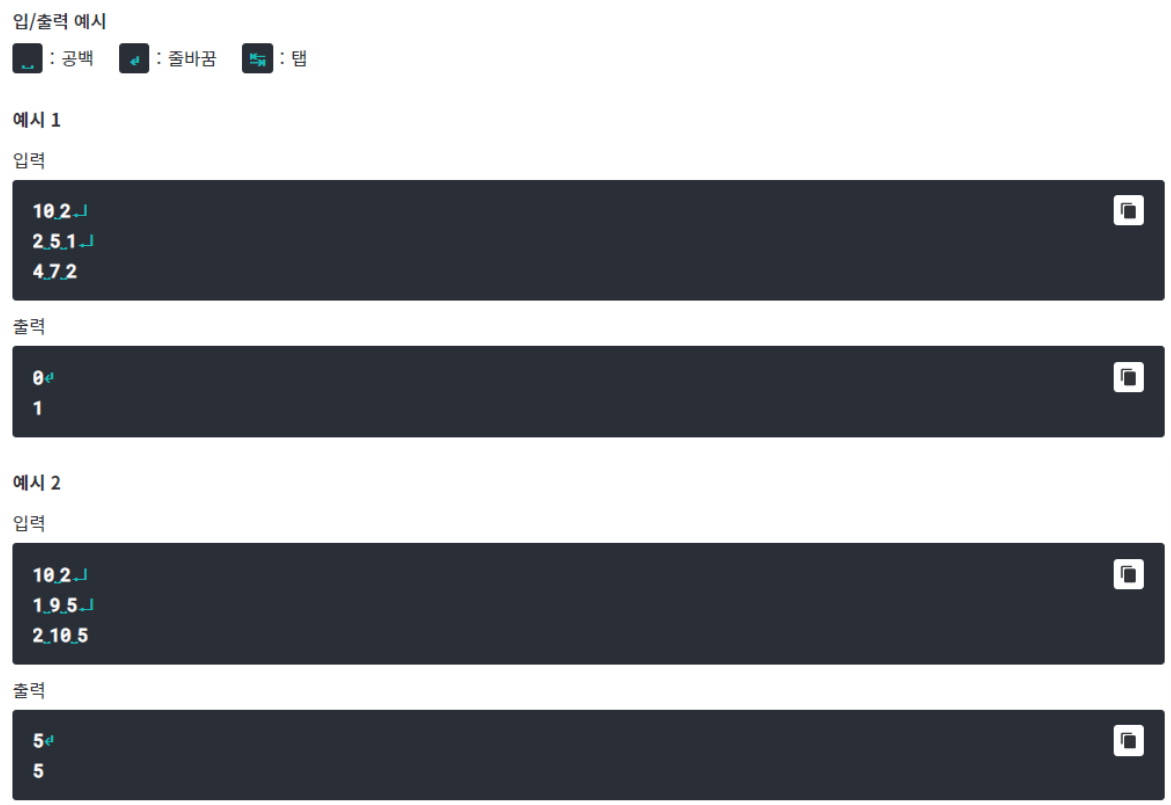
• 앞서 해결한 문제의 조금 더 복잡한 버전이다.
• 우선 left, right, color 등을 편하게 관리하기 위해 Painting 클래스를 생성했다.
• 그리고 m회의 색칠 정보를 입력받은 후 left, right를 -1씩 해줘 0~n-1로 맞춰주었다.

solve 메소드

• 먼저 전달받은 좌석의 수 n을 사용해 seats 배열을 생성했다.
• 그리고 m회 색칠하면서 for문 중첩을 통해 left~right 까지 color로 seats 배열에 색깔 정보를 담았다.
• 이제 0~99번 색깔의 정보를 담은 카운팅 배열 table을 선언하고, 카운팅 정렬을 해준다. 이러면 table은 n개의 seats색을 인덱스로 카운팅하게 된다.
• 이제 카운트가 0인 색을 제외하고, 전체 table을 탐색한다.
• max/minColor 색과 i색을 table의 인덱스로 넣어, 카운트가 더 큰/작은 것으로 갱신해 나간다.
• 이후 이를 두줄로 출력하면 끝이다. 꼭 마지막에 동적할당했던 seats, table 배열을 delete 해줘야 한다.

#include <stdio.h>
#include <iostream>
using namespace std;
//0~99의 색을 사용해 1~n까지의 의자에 페인트를 칠한다.

const int MAX_COLOR_NUMBER = 100;//색깔 수

//좌석 1회 색칠에 대한 정보 클래스
class Painting {
public:
    int left;
    int right;
    int color;

    //기본생성자
    Painting() {}

    Painting(int left, int right, int color) {
        this->left = left;
        this->right = right;
        this->color = color;
    }
};

//카운팅 정렬 수행 함수
void fillFrequencyTable(int data[], int n, int table[]) {

    //n개의 좌석 각각의 색깔을 인덱스로 해
    //0~99의 색깔 배열을 카운팅 
    for (int i = 0; i < n; i++) {
        table[data[i]]++;
    }
}

//가장 많은 좌석이 가진 색, 가장 적은 좌석이 가진 색 번호 출력
//여러개인 경우 작은 번호 출력
int solve(int n, int m, const Painting paint[]) {

    //n개의 좌석 배열 생성, 초기값 0번 색칠
    int* seats = new int[n] {};

    //좌석을 m번 칠함
    for (int i = 0; i < m; i++) {
        //m개의 paint[]마다 left~right까지 색을 color로 칠함
        for (int j = paint[i].left; j <= paint[i].right; j++) {
            seats[j] = paint[i].color;
        }
    }

    //0~99번 색까지의 카운팅 배열 선언(기본값 0)
    int* table = new int[MAX_COLOR_NUMBER] {};
    //카운팅 정렬 수행
    fillFrequencyTable(seats, n, table);

    int minColor = seats[0];//카운팅 최댓값(최대 색 번호)
    int maxColor = seats[0];//카운팅 최소값(최소 색 번호)

    //색번호 0~99번 까지 table 배열을 탐색하며
    for (int i = 0; i < MAX_COLOR_NUMBER; i++) {
        
        //한번도 칠하지 않은 색은 skip해 연산량 감소
        if (table[i] == 0) {
            continue;
        }

        //max/minColor와 i색 중 빈도수 큰/작은 것으로 갱신
        //단, 같은 경우(<=) 갱신x하므로 작은 번호 색만 담기게 됨
        if (table[maxColor] < table[i]) {
            maxColor = i;
        }
        if (table[minColor] > table[seats[i]]) {
            minColor = i;
        }
    }

    cout << maxColor << endl;
    cout << minColor << endl;
    delete[] seats;
    delete[] table;
}

int main() {
    int n, m;
    cin >> n >> m;

    //m회의 색칠정보를 저장할 배열
    Painting* paint = new Painting[m];

    //m회의 페인트 칠할 경우를 입력
    //(left~right번까지 color색으로)
    for (int i = 0; i < m; i++) {
        cin >> paint[i].left >> paint[i].right >> paint[i].color;

        //좌석 번호 1~n입력이므로, -1해서 0~n-1로 맞춰줌
        paint[i].left -= 1;
        paint[i].right -= 1;
    }

    //정답 구함
    solve(n, m, paint);

    return 0;
}

3. 응모 - vector<> 자료구조

풀이

• 이번 문제는 vector를 사용해서 해결해 볼 것이다. 먼저 벡터의 멤버 함수는 아래와 같다.

vector<int> v(5);// 기본값 0인 5개 원소 배열
vector<int> v(5,2);// 기본값 2인 5개 원소 배열

v.size();// 원소 개수 반환
v.clear();// 모든 원소 제거(메모리는 유지)
v.resize(n,3);// 크기를 n으로 변경하고, 모든 값 3으로 초기화
v.push_back(7);// 마지막 원소 뒤에 7 삽입

• 벡터를 배열 대신 사용하는 것 말고는 크게 다르지 않다.
• 단순히 입력받은 n개의 시리얼 번호 data를 인덱스로 넣어 카운팅 정렬을 해준 뒤, table 전체를 탐색하며 1번만 나온 시리얼 번호를 ret 벡터에 넣어 반환하면 된다.

#include <stdio.h>
#include <iostream>
#include <vector>
using namespace std;

const int MAX_SERIAL_NUMBER = 100000;//시리얼 번호 최대값

//카운팅 정렬 수행 함수
void fillFrequencyTable(const vector<int> &data, int n, vector<int> &table) {
    
    table.clear();
    table.resize(MAX_SERIAL_NUMBER + 1, 0);//크기와 기본값 초기화

    //n개의 데이터를 인덱스로 해
    //0~10만의 시리얼 번호 배열을 카운팅 
    for (int i = 0; i < n; i++) {
        table[data[i]]++;
    }
}

//유일한 시리얼 번호만 추려 출력
vector<int> getUniqueElements(const vector<int> &data, int n) {
    
    //유일한 원소들 배열
    vector<int> ret;

    //1~10만 카운팅 배열 선언
    vector<int> table;
    fillFrequencyTable(data, n, table);

    //카운팅 정렬된 table 배열을 탐색하며
    for (int i = 1; i < MAX_SERIAL_NUMBER; i++) {
        //1번 나온 시리얼 번호만
        if (table[i] == 1) {
            ret.push_back(i);//결과 벡터에 삽입
        }
    }
    return ret;
}
    
int main() {
    int n;
    //시리얼 번호 수 n 입력
    cin >> n;

    vector<int> data = vector<int>(n);
    //n개의 시리얼 번호 입력
    for (int i = 0; i < n; i++) {
        cin >> data[i];
    }

    //중복 시리얼 번호 제외, 나머지 번호 공백구분 출력
    const vector<int> result = getUniqueElements(data, n);

    //result 크기만큼 결과 출력
    for (int i = 0; i < result.size(); i++) {
        cout << result[i] << " ";
    }

    return 0;
}

4. 피보나치

풀이

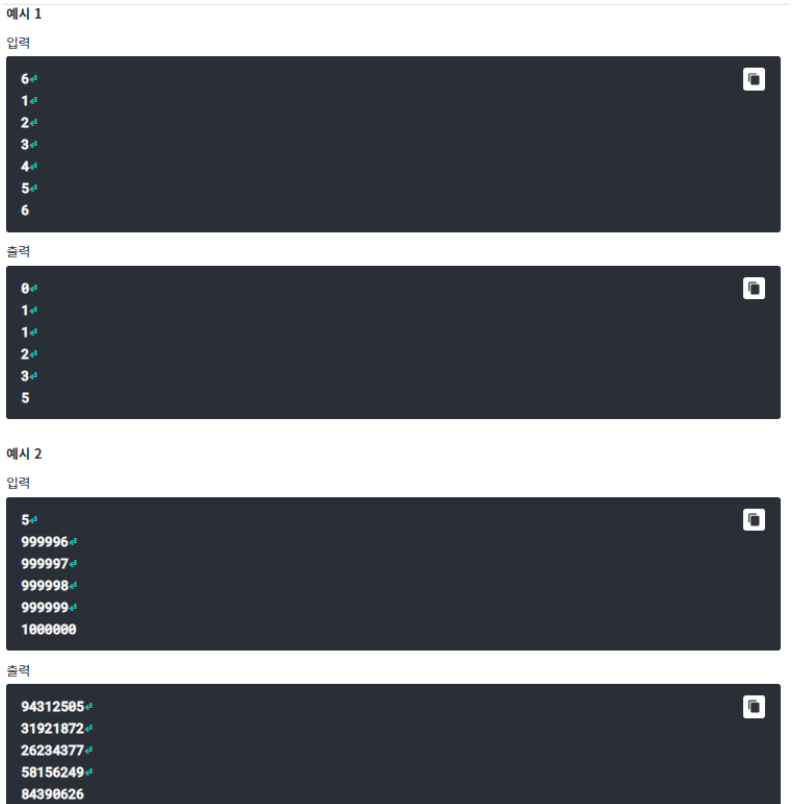
• 먼저 나중에 계속 사용할 수 있도록 피보나치 벡터를 전역변수로 선언해주고, main 첫줄에서 문제의 최대 크기로 피보나치 수열 벡터 FIBONACCI_TABLE을 생성해 준다.
• 결과를 반환할 ret 벡터를 최대크기보다 1크게 선언해주고, 공식에 따라 for문으로 ret 벡터에 수열 값을 대입해줬다.
• 그리고 출력 형식을 보면 아래 8자리만 출력하면 된다고 했으므로, 간단히 ret[i] % 10^8을 해줘서 넣어야 한다.
  " (a % MOD) + (b % MOD) == (a + b) % MOD가 성립하므로 이렇게 매번 해줘도 피보나치 수열에는 지장이 없다.
• 이제 getFibo 메소드를 호출해 이 벡터에서 n번째 피보나치 수열을 반환받아 출력하면 된다.

#include <stdio.h>
#include <iostream>
#include <vector>
using namespace std;

const int MAX_N = 1000000;//최대 피보나치 크기
vector<int> FIBONACCI_TABLE;//앞으로 계속 쓸 피보나치 벡터 전역변수


//n까지의 피보나치 수열 벡터를 만들어 반환하는 함수
vector<int> makeFibonacciTable(int n) {
    const int MOD = 100000000;//10^8

    //피보나치 배열 ret은 1부터 시작(1~10만)
    vector<int> ret(n + 1);
    ret[1] = 0;//첫 항
    ret[2] = 1;//두번째 항

    //f(n) = f(n-1) + f(n-2)
    for (int i = 3; i <= n; i++) {
        ret[i] = ret[i - 1] + ret[i - 2];
        
        ret[i] %= MOD;//아래 8자리만 추출
;   }
    return ret;
}

//미리 만들어 둔 피보나치 수열 중 n번째 피보나치 수열 반환 함수
int getFibo(int n) {

    int result = FIBONACCI_TABLE[n];

    return result;
}

int main() {
    //피보나치 수열을 최대 크기만큼 미리 만들어 전처리 해둠
    FIBONACCI_TABLE = makeFibonacciTable(MAX_N);

    int t;
    //테스트 케이스 수 t 입력
    cin >> t;

    //t개의 정수 n 입력
    for (int i = 0; i < t; i++) {
        int n;
        cin >> n;

        //n번째 피보나치 수열 리턴
        int result = getFibo(n);
        cout << result << endl;
    }

    FIBONACCI_TABLE.clear();
    return 0;
}