문제 링크

문제 링크

---

< 문제 핵심 >

1. 현재 위치

   → 현재 위치에 따라 cmd가 실행되므로 현재 위치를 아는 것이 중요

2. cmd 실행

   1. D,U 단순히 현재 위치가 계속 바뀌는 것

   2. Z 실행 시 최근 삭제된 순서대로 복원

      → delete_stack를 따로 생성 ⇒ 몇번째 인덱스들이 삭제되었는지 파악

      → stack의 후입선출 활용하여 append,pop

   3. 예외 처리 : C 실행 시 현재위치가 마지막 행일 경우

      → 삭제 후에도 현재 위치는 마지막 행이어야 함

3. list형태를 문자열로 Join하여 리턴

---

< 문제 아이디어 >

• 인덱스를 이용
• heapq 사용
• linked list 사용
• • deque 사용

---

< 코드 >

1. 인덱스 사용

def solution(nmd):
    table = [ i for i in range(n)]
    ox_table = ["O"]* n
    location = table[k]
    deleted_stack = []
    for i in cmd :
        idx = table.index(location)

        if "D" in i :
            move = int(i.split()[1])
            location = table[idx+move]
        elif "U" in i :
            move = int(i.split()[1])
            location = table[idx-move]
        elif "C" in i :
            if location == table[-1] :
                location = table[-2]
                idx = table.index(location)
                deleted_stack.append(table.pop(idx+ 1))
            else :
                location = table[idx+1]
                idx = table.index(location)
                deleted_stack.append(table.pop(idx-1))
        elif "Z" in i :
            table.append(deleted_stack.pop())
            table.sort()

    for i in deleted_stack :
        ox_table[i] = "X"

    return "".join(ox_table)

2. heapq 사용

import heapq

def inverse(num):
    return -num

def solution(n, k, cmds):
    max_heap = list(map(inverse, range(k)))
    min_heap = list(range(k, n))
    heapq.heapify(max_heap)
    heapq.heapify(min_heap)

    table = ['O' for _ in range(n)]
    deleted_stack = []

    for cmd in cmds:
        command = cmd.split()
        command1 = command[0]

        # U 과 D
        if command1 == "D":
            num = int(command[1])
            for _ in range(num):
                heapq.heappush(max_heap, -heapq.heappop(min_heap))
        elif command1 == "U":
            num = int(command[1])
            for _ in range(num):
                heapq.heappush(min_heap, -heapq.heappop(max_heap))

        # C 와 Z
        elif command1 == 'C':
            delete_num = heapq.heappop(min_heap)
            deleted_stack.append(delete_num)
            table[delete_num] = 'X'
            if len(min_heap) == 0:
                heapq.heappush(min_heap, -heapq.heappop(max_heap))
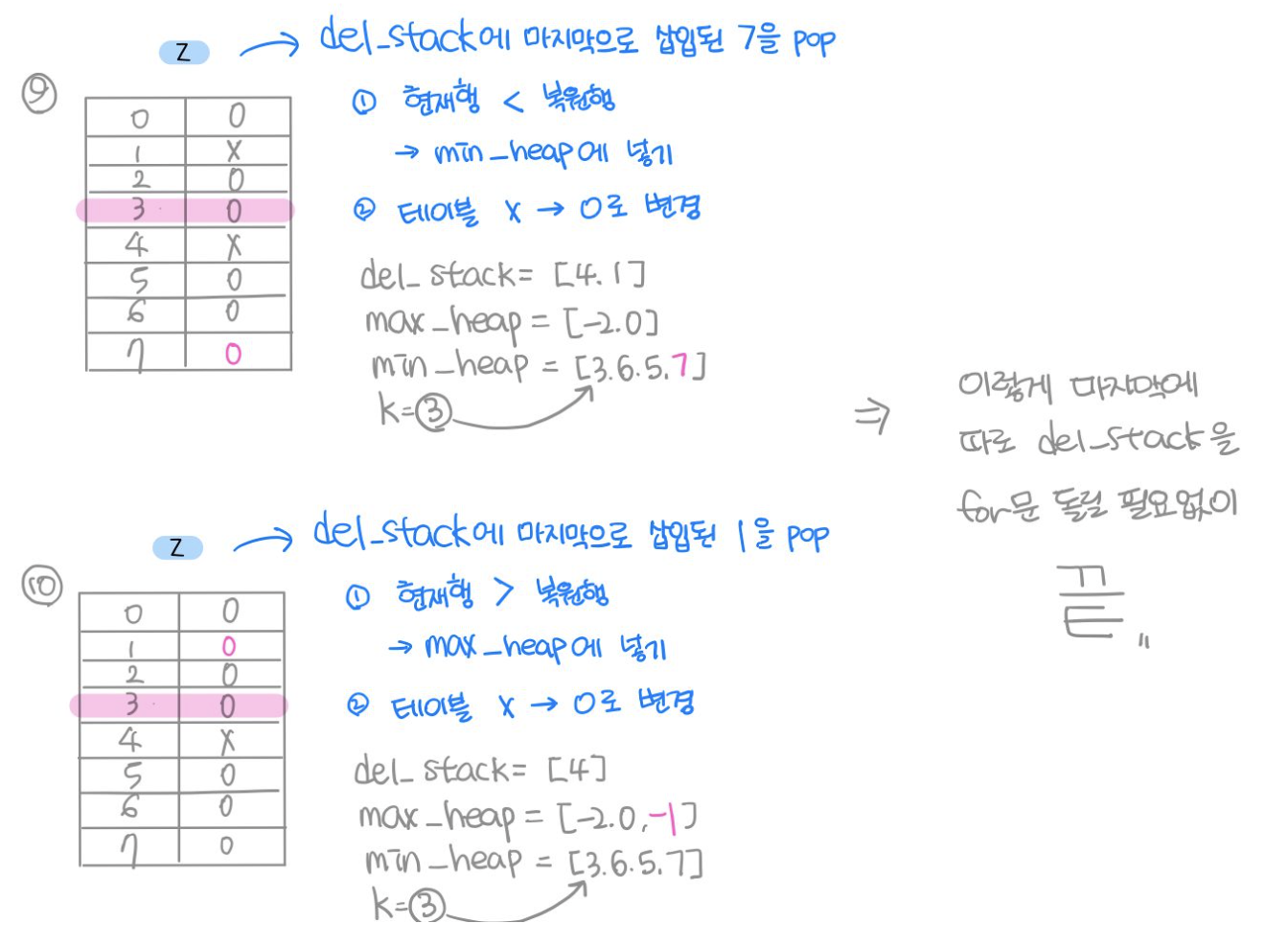
        elif command1 == 'Z':
            restore_num = deleted_stack.pop()
            table[restore_num] = 'O'
            if min_heap[0] > restore_num:
                heapq.heappush(max_heap, -restore_num)
            else:
                heapq.heappush(min_heap, restore_num)

    return ''.join(table)

3. deque 추가

import heapq
from collections import deque

def inverse(num):
    return -num

def solution(n, k, cmds):
    max_heap = list(map(inverse, range(k)))
    min_heap = list(range(k, n))
    heapq.heapify(max_heap)
    heapq.heapify(min_heap)

    table = ['O' for _ in range(n)]
    deleted_stack = deque()

    for cmd in cmds:
        command = cmd.split()
        command1 = command[0]

        # U 과 D
        if command1 == "D":
            num = int(command[1])
            for _ in range(num):
                heapq.heappush(max_heap, -heapq.heappop(min_heap))
        elif command1 == "U":
            num = int(command[1])
            for _ in range(num):
                heapq.heappush(min_heap, -heapq.heappop(max_heap))

        # C 와 Z
        elif command1 == 'C':
            delete_num = heapq.heappop(min_heap)
            deleted_stack.append(delete_num)
            table[delete_num] = 'X'
            if len(min_heap) == 0:
                heapq.heappush(min_heap, -heapq.heappop(max_heap))
        elif command1 == 'Z':
            restore_num = deleted_stack.pop()
            table[restore_num] = 'O'
            if min_heap[0] > restore_num:
                heapq.heappush(max_heap, -restore_num)
            else:
                heapq.heappush(min_heap, restore_num)

    return ''.join(table)

---

< 구현 방식 >

( 사용한 메소드, 라이브러리 등 원리 )

1. 인덱스 사용

• 바뀐 현재위치의 인덱스를 찾아 idx에 저장

• stack의 후입선출을 이용하여 delete_stack에 삽입,삭제

• Z 복원 시 table에 삽입 후 sort을 통해 원래 위치로 갈 수 있도록 설정

• C 실행 시 현재 위치가 마지막 행의 위치와 동일한지 table[-1]로 확인

  → 현재 위치를 table[-2]로 설정

• ox_table을 처음에 모두 "O"로 초기화

  → cmd 모두 실행 후 delete_stack에 남아있는 삭제된 행(i)들을 for문을 돌린다

  → 해당 행들을 ox_table[i] = "X" 로 바꿈

• join을 통해 리턴

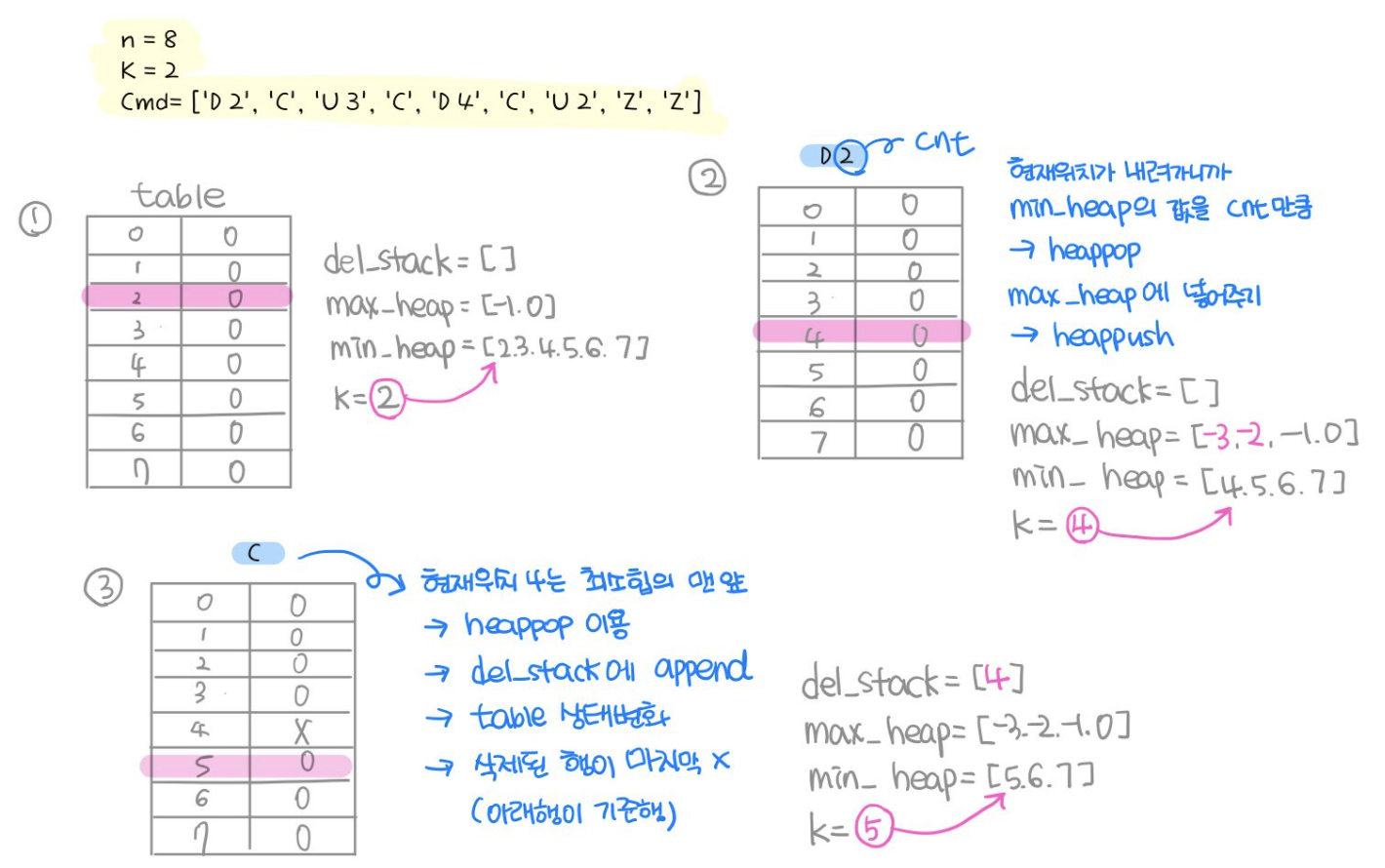
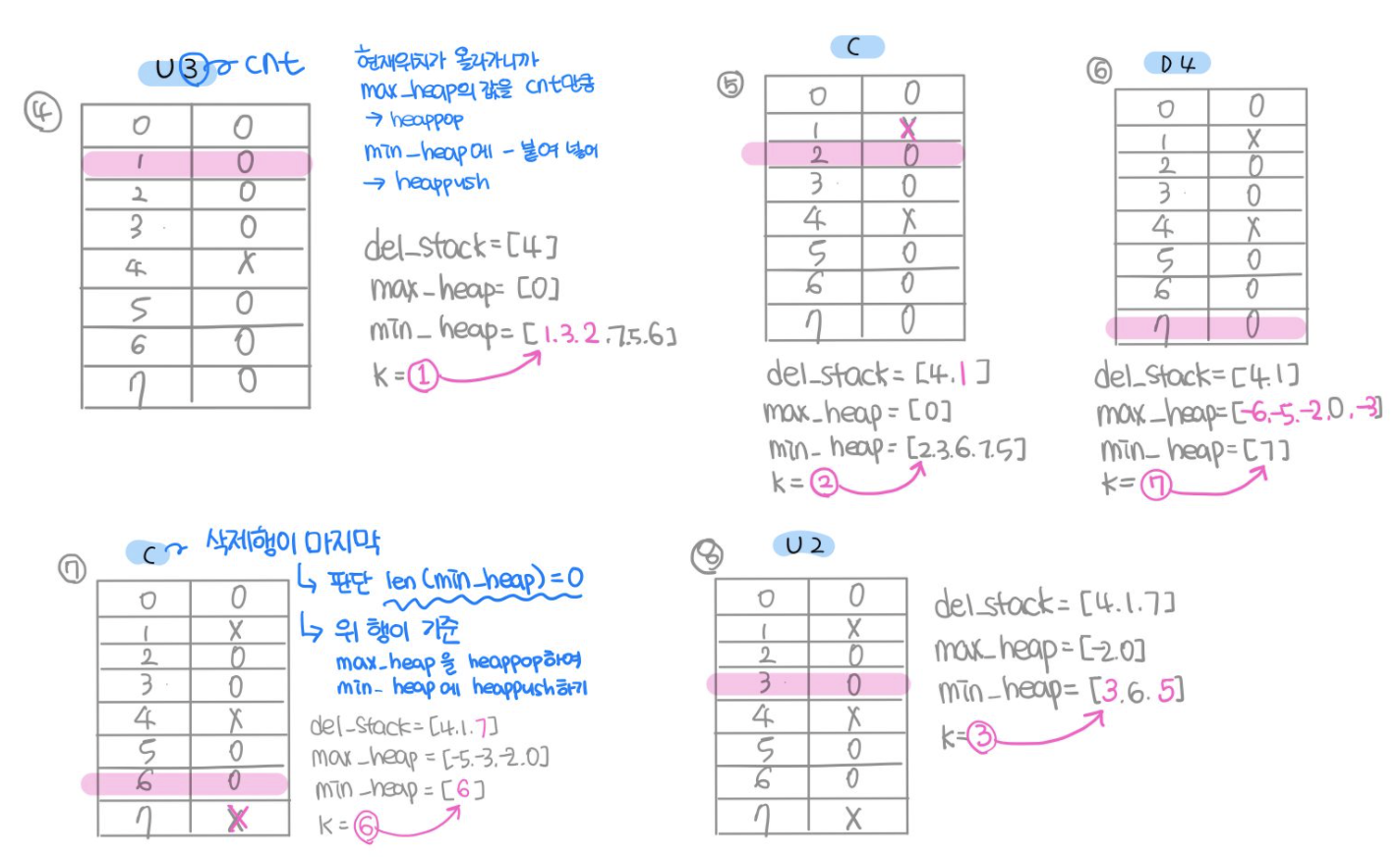
2. heapq 사용

1. 최대힙, 최소힙 사용하기

• 최대힙은 현재 위치 전까지 (0~k-1)

• 최소힙은 현재 위치부터 나머지 (k~n-1)

  • inverse 메소드 생성 후 이용하는 이유

    최대힙은 heapq 모듈에는 없어서 최소힙을 약간 응용해야 하는데 힙에 원소를 추가하거나 삭제하면 리스트 내에서는 맨 앞에 있는 값을 기준으로 최소 힙이 구성된다. 즉 값이 크면 -를 붙여 가장 작은 값으로 만들 수 있으므로 값에 -를 붙여 최대힙을 만든다.

  • 최대힙,최소힙을 사용하는 이유

    항상 현재 위치는 최소힙을 맨 앞 부분

    ( 즉, 최소힙의 뒷부분은 현재 위치보다 큰 값들중 삭제되지 않은 행들을 보관하기 위한 용도 )

    ( 최대힙은 현재 위치보다 작은 값들중 삭제되지 않은 행들을 보관하기 위한 용도 )

    

    → 최대힙을 pop했을 경우 현재 위치 직전 행의 값이 pop이 됨

    → 최소힙을 pop했을 경우 현재 위치가 pop이 됨

2. deleted_stack 생성

• 순차적으로 삭제된 인덱스 담는 배열 생성
• stack의 후입선출을 이용하여 append,pop 사용

3. OX를 담는 table 생성

• 모든 행과 상태를 표시하는 배열 생성
• 처음에는 "O"로 초기화
• 삭제시 삭제부분 "O"→"X"로 변경
• 복원시 복원부분 "X"→"O"로 변경
• 마지막에는 join으로 리스트 → 문자열로 변경하여 리턴

---

3. deque 추가

• 정확성, 효율성 큰 차이가 없음

  → 왜? deque 이용 부분이 적음

  전체적인 코드 부분은 heapq를 사용
  delete_stack 부분만 deque 사용

• 정확성 시간은 대부분 단축

• 효율성 시간은 오히려 증가

---

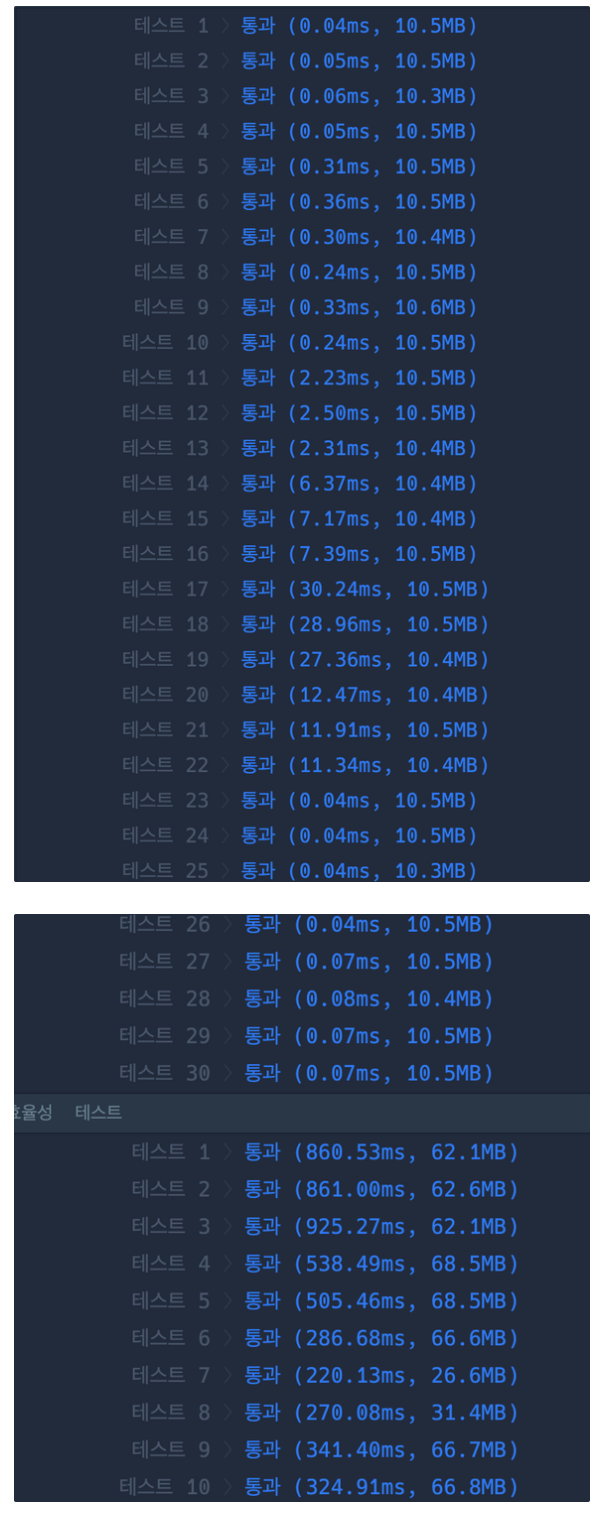
< 결과 >

1. 인덱스 사용

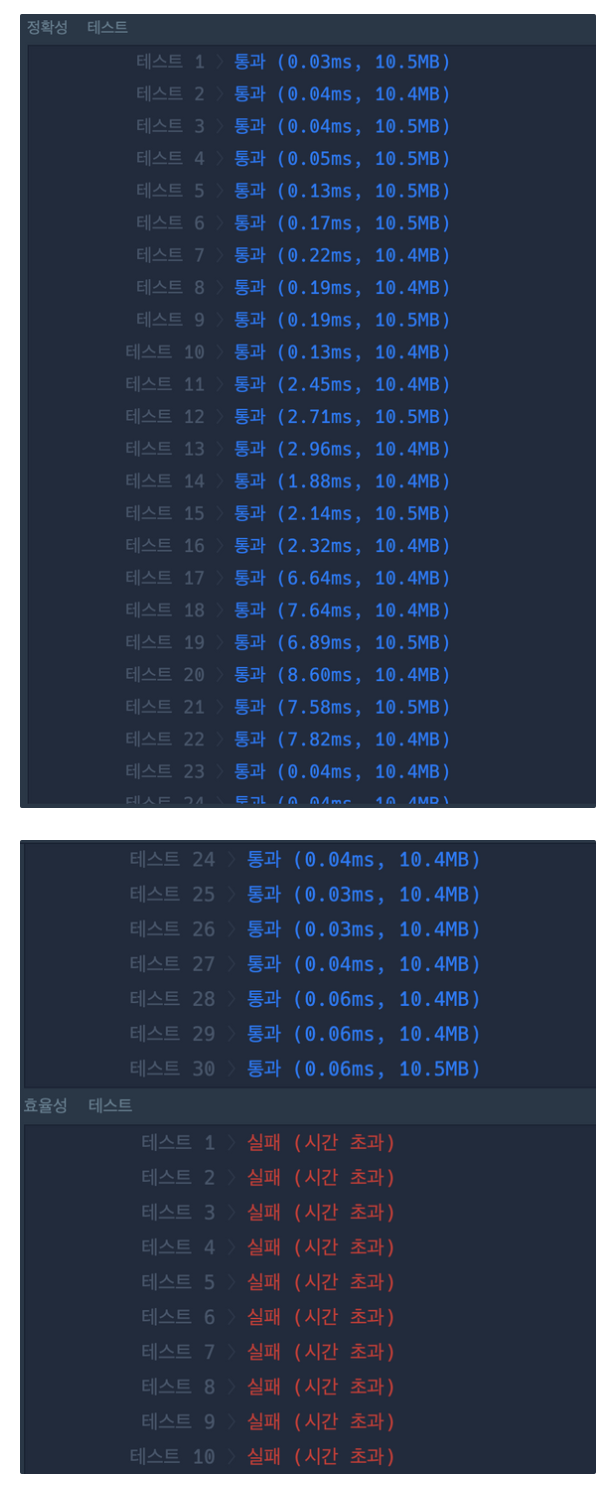
2. heapq 사용

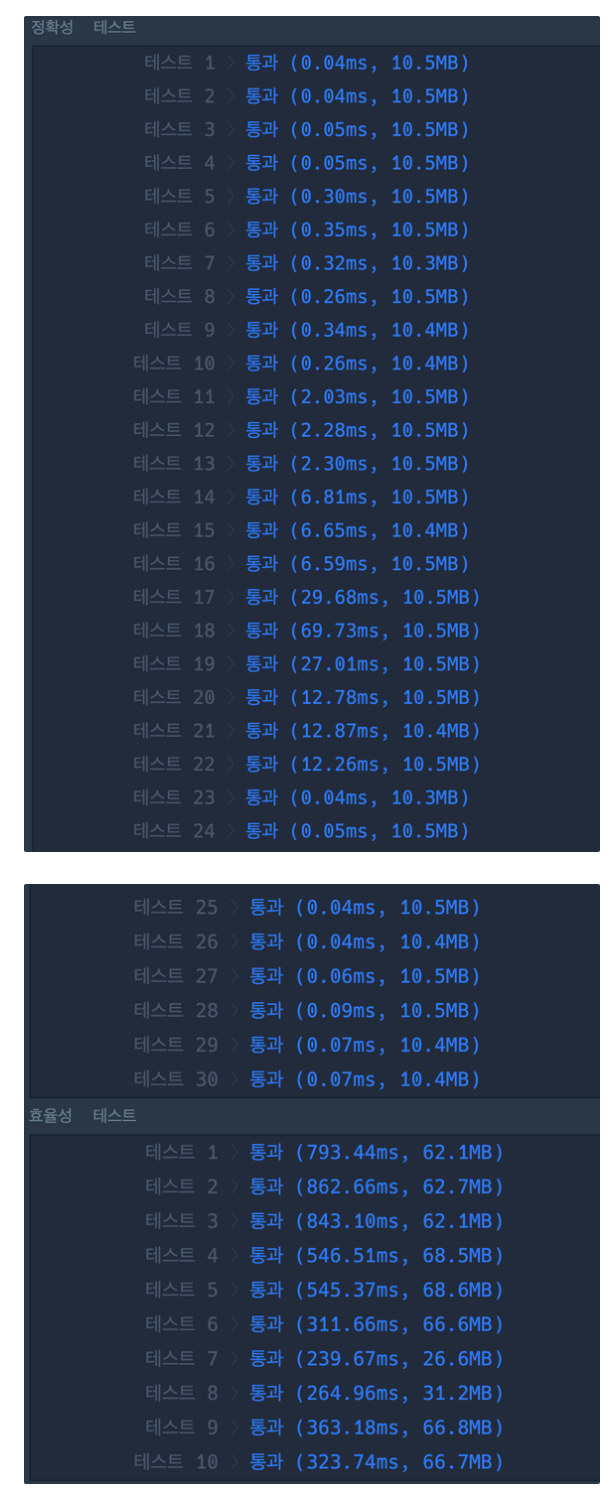
3. deque 추가