---

< 문제 이해 >

• A,B 모두 택시를 타고 귀가하는데 소요되는 최저 택시 요금 구하기!

• 합승해서 이동할 수 있는 경로의 비용 ( together ) + 각각 혼자 택시타고 이동할 수 있는 경로의 비용 ( A + B )

• 만약, 처음부터 합승하지 않고 각자 이동하는 경우의 택시 요금이 낮다면, 합승하지 않아도 됨

• s = 출발지점

  a = A의 도착지점

  b = B의 도착지점

  fares 의 각 행 [c,d,f] → c지점과 d지점 사이의 예상 택시비

• return → 택시비 최소 비용

---

< 문제 핵심 >

1. 다익스트라 , 플로이드 와샬 이용

   • 정점 사이의 최단경로 찾기

2. 각 경로와 비용을 저장할 배열 생성

   • 비용을 기준으로 오름차순 정렬하기

3. 합승하여 가는 경우 , 각자 집에 가는 경우, 한 사람 A 집 가는 중 다른 사람 B를 중간에 내려주는 경우

   • routes 배열 생성하여 방문한 섬을 넣기

4. 최종 비용

   • answer에 이전 비용과 현재 비용을 비교하여 더 작은 값으로 교체

---

< 문제 아이디어 >

• 다익스트라 알고리즘
• 플로이드 와샬

---

< 코드 >

1. 다익스트라 알고리즘

import heapq as hq
INF = int(1e9)

def dijkstra(distances, start, graph) :
    queue = []
    distances[start] = 0
    hq.heappush(queue, (distances[start], start))
    while queue:
        current_distance, current = hq.heappop(queue)
        if distances[current] < current_distance :
            continue
        for adj_node, next_distance in graph[current] :
            cost = current_distance + next_distance
            if cost < distances[adj_node] :
                distances[adj_node] = cost
                hq.heappush(queue,(distances[adj_node],adj_node))

def solution(n, s, a, b, fares):
    answer = INF
    graph = [[] for _ in range(n+1)]
    for fare in fares :
        x,y,cost = fare
        graph[x].append((y,cost))
        graph[y].append((x,cost)

    distance = [INF]*(n+1)
    dijkstra(distance,s,graph)

    for i in range(1,n+1) :
        route = [INF]*(n+1)
        dijkstra(route,i,graph)
        answer = min(answer, distance[i] + route[a] + route[b])

    return answer

2. 플로이드 와샬 알고리즘

def solution(n, s, a, b, fares):
    INF = int(1e9)
    answer = INF
    distance = [[INF] * (n + 1) for _ in range(n + 1)]

    for i in range(1, n + 1):
        distance[i][i] = 0
    for x, y, cost in fares:
        distance[x][y] = distance[y][x] = cost

    for k in range(1, n + 1):
        for i in range(1, n + 1):
            for j in range(1, n + 1):
                if distance[i][j] > distance[i][k] + distance[k][j]:
                    distance[i][j] = distance[i][k] + distance[k][j]

    for i in range(1, n + 1):
        answer = min(answer, distance[s][i] + distance[i][a] + distance[i][b])
    return answer

---

< 구현 방식 >

( 사용한 메소드, 라이브러리 등 원리 )

1. 다익스트라 사용

1. graph 배열 생성

• 인접 행렬 생성
• x → y 와 y → x 로 가는 비용이 동일하다고 나와있으므로 아래와 같이 만듬

graph = [[] for _ in range(n+1)]
    for fare in fares :
        x,y,cost = fare
        graph[x].append((y,cost))
        graph[y].append((x,cost))

2. 다익스트라 이용

• 다익스트라는 최단 경로 알고리즘으로 특정 노드에서 시작해 모든 노드까지 도착할 수 있는 가장 짧은 경로

  • greedy 알고리즘
  • 현재 상황에서 최선의 선택을 진행 , BFS 방식과 유사
  • 시작 노드에서 모든 노드간의 거리 값을 저장하는 배열을 생성한 다음, 인접한 노드들의 거리를 구해 가장 짧은 경로를 해당 배열에 업데이트 해나가는 방식
  • 우선 순위 큐 ⇒ 최소 힙 사용

• 모든 거리를 무한대로 초기화 시킨 후 다익스트라 적용하여 s 지점에서 나머지 정점까지의 최단거리 구하기

  		distance = [INF]*(n+1)
      dijkstra(distance,s,graph)

3. 경유지점 찾기

• 1번부터 n번까지의 경유지점을 for문으로 한번씩 지정하기
  • 모든 거리를 무한대로 초기화 시킨 route를 임시로 생성
  • 시작점을 i지점으로 설정한 후 다익스트라 적용하여 i 지점에서 나머지 정점까지의 최단거리 구하기
  • i 지점까지 이동 후 각자 목적지까지 가는 경로 비용 distance[i] + route[a] + route[b] ⇒ 💰로 설정
  • 💰이 이전 구했던 값보다 더 작다면 answer 값을 갱신함

for i in range(1,n+1) :
        route = [INF]*(n+1)
        dijkstra(route,i,graph)
        answer = min(answer, distance[i] + route[a] + route[b])

4. 최종 비용

• 최종 answer를 return

---

2. 플로이드 와샬 사용

1. graph 배열 생성

• 인접 행렬 생성
• x → y 와 y → x 로 가는 비용이 동일하다고 나와있으므로 아래와 같이 만듬

    distance = [[INF] * (n + 1) for _ in range(n + 1)]

    for i in range(1, n + 1):
        distance[i][i] = 0

    for x, y, cost in fares:
        distance[x][y] = distance[y][x] = cost

2. 플로이드 와샬 이용

• 플로이드는 모든 정점에서 모든 정점으로의 최단 경로

    for k in range(1, n + 1):
        for i in range(1, n + 1):
            for j in range(1, n + 1):
                if distance[i][j] > distance[i][k] + distance[k][j]:
                    distance[i][j] = distance[i][k] + distance[k][j]

3. 경유지점 찾기

   for i in range(1, n + 1):
        answer = min(answer, distance[s][i] + distance[i][a] + distance[i][b])

• 1번부터 n번까지의 경유지점을 for문으로 한번씩 지정하기
  • 시작지점 ~ 경유지점 + 경유지점 ~ A도착지점 + 경유지점 ~ B도착지점 ⇒ 💰로 설정
  • 💰이 이전 구했던 값보다 더 작다면 answer 값을 갱신함

4. 최종 비용

• 최종 answer를 return

---

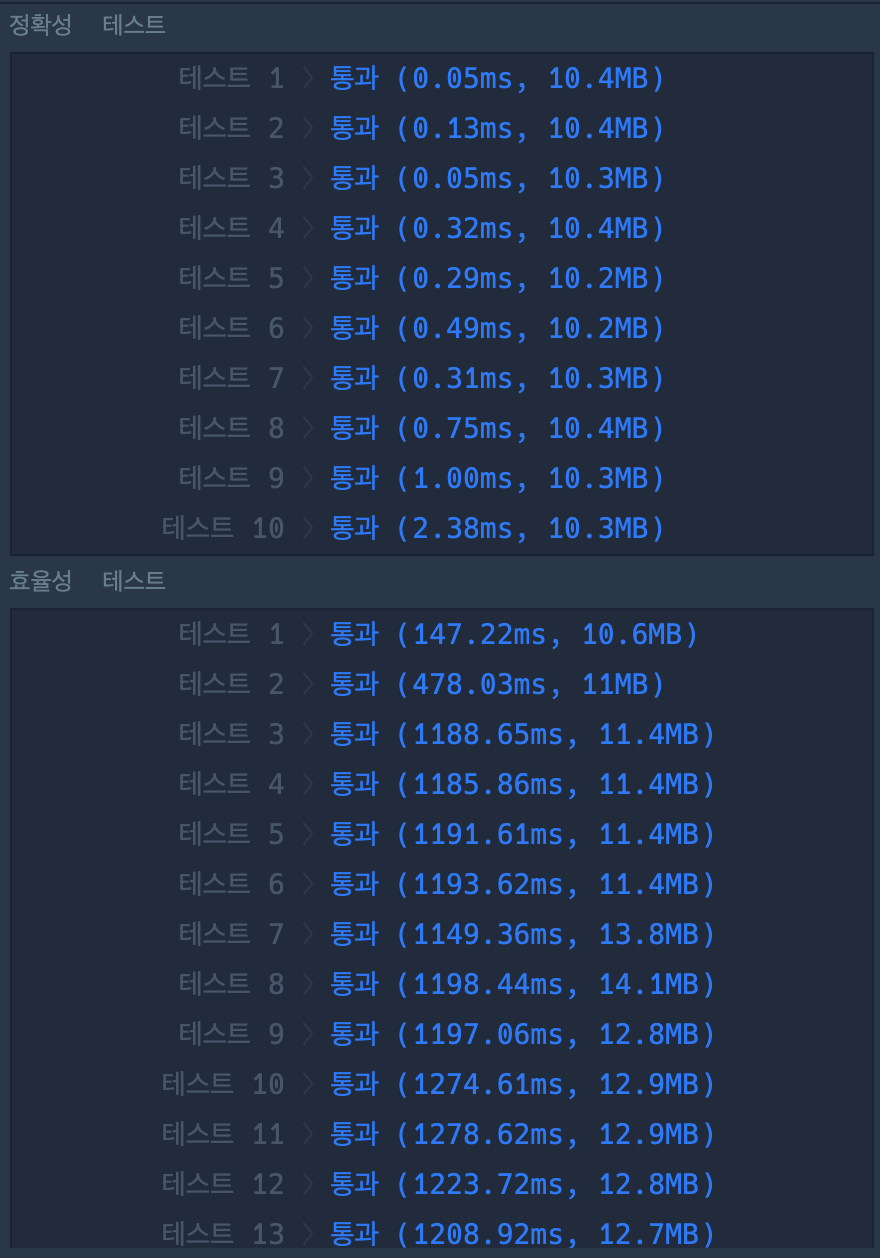
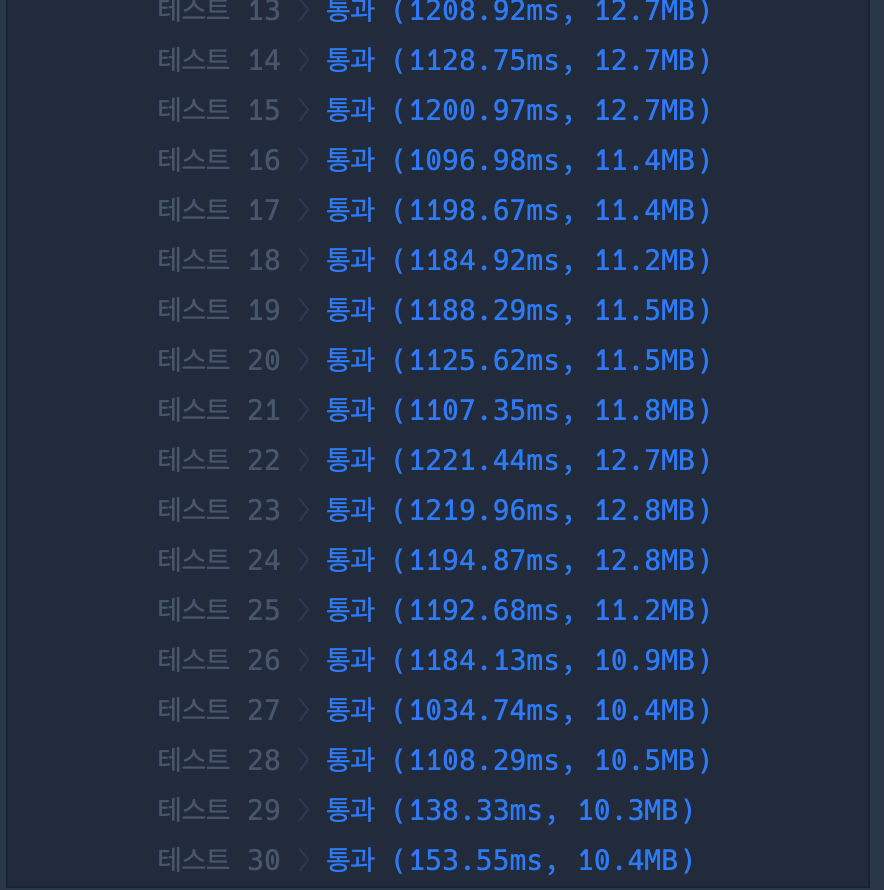
< 결과 >

1. 다익스트라 사용

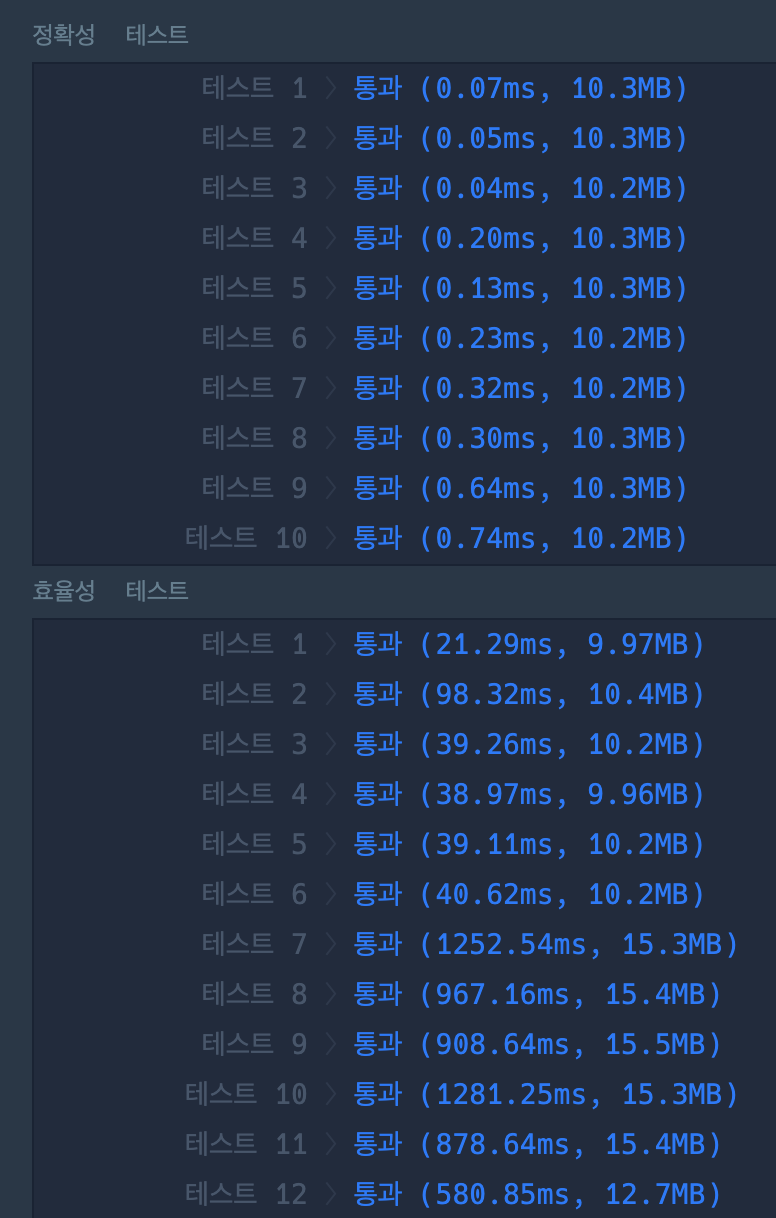
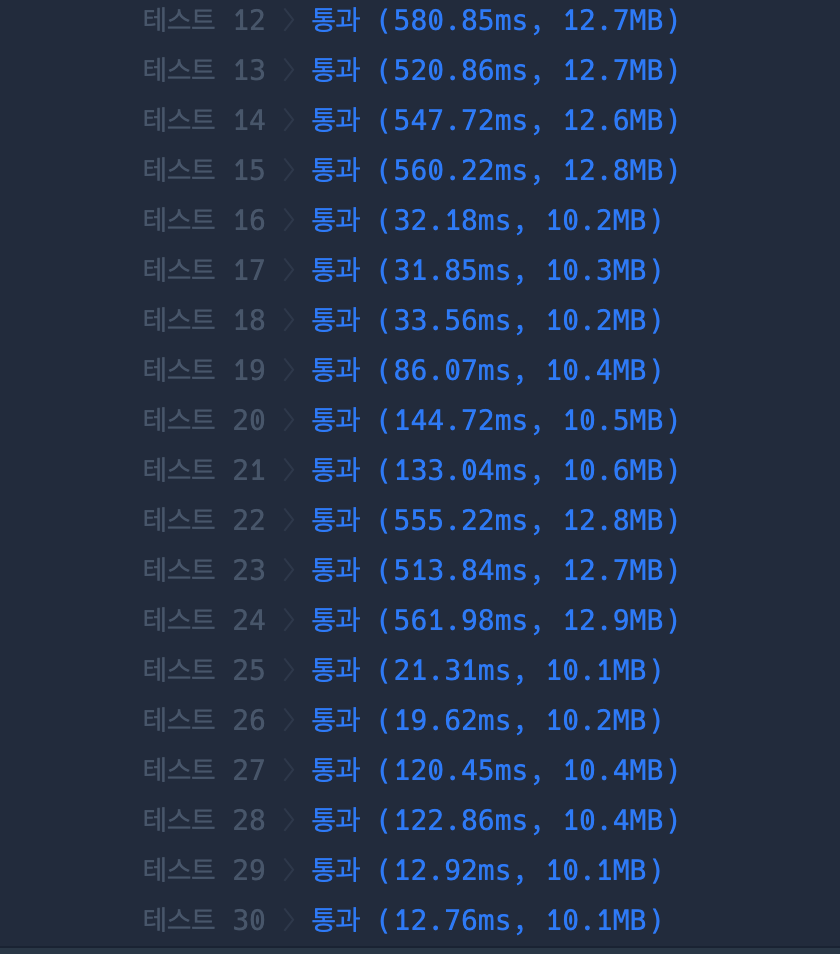
2. 플로이드 와샬 알고리즘