자릿수 더하기

Ha young, Kim·2021년 8월 3일

algorithm

목록 보기

1/1

자릿수 더하기

본 글은 프로그래머스의 무료 강의 알고리즘 문제 해설을 공부하며 작성한 내용입니다.

문제 설명

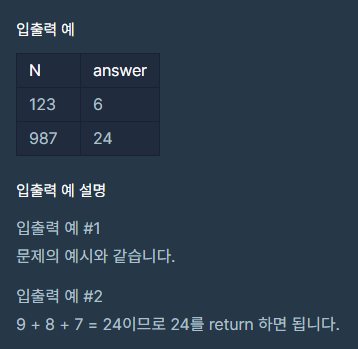
자연수 N이 주어지면, N의 각 자릿수의 합을 구해서 return 하는 solution 함수를 만들어 주세요.
예를들어 N = 123이면 1 + 2 + 3 = 6을 return 하면 됩니다.

제한사항

N의 범위 : 100,000,000 이하의 자연수

문제 예시

keywords

toString() , split() , map() , Number() , reduce() , 자연수

문제 풀이

123 이라는 숫자를 받으면, [1, 2, 3] 이라는 배열로 바꿔준 다음, 각각의 배열 안 요소들을 더하여 그 합6을 구하면 된다.

먼저 숫자를 배열로 바꾸기 위해서는, toString() 함수를 사용하여 문자열로 바꿔주어야 한다.

function solution(n) // 123
{
	let digits = n.toString() // "123"
}

문자열을 배열로 바꿔주는 split() 함수는 숫자에는 사용할 수 없기 때문이다. 이제 문자열을 배열로 바꿔준다.

function solution(n) // 123
{
	let digits = n.toString().split("") // "123" -> ["1", "2", "3"]
}

split(seperator) 함수의 seperator 에 "" 처럼 빈 문자열을 주었을 경우, 원본 문자열의 각각의 문자가 배열의 원소 하나씩으로 반환된다.

이제 반환된 문자들의 배열을 숫자들의 배열로 바꿔준다. map() 함수로 배열안의 요소들에 Number() wrapper 객체를 사용하여 새로운 배열로 바꿔 주었다.

function solution(n) // 123
{
	let digits = n.toString().split("").map(item => Number(item));
  	// "123" -> ["1", "2", "3"] -> [1, 2, 3]
}

배열의 요소들의 총 합을 구하는 방법은 for loop 을 사용하거나, lodash 라이브러리의 sum 함수를 사용하는 방법도 있다. 여기서는 javascript 의 내장함수인 reduce() 를 사용했다.

function solution(n) // 123
{
	let digits = n.toString().split("").map(item => Number(item));
  	// "123" -> ["1", "2", "3"] -> [1, 2, 3]
  	const result = digits.reduce((accumulator, currentValue) => accumulator + currentValue,0);
  	// 누적값:0 + 현재값:1 -> 누적값:1
  	// 누적값:1 + 현재값:2 -> 누적값:3
  	// 누적값:3 + 현재값:3 -> 결과값:6
        return result;
}

reduce 함수는 reducer 함수를 실행하고, 하나의 결과 값을 반환한다. reducer 함수는 누적값과 현재값을 가질 수 있다(선택사항으로 현재 index 와 원본 배열을 받을 수도 있지만, 생략 가능하다).

이제 n의 범위를 정해준다.

function solution(n)
{
    if(n<100_000_000){
        let digits = n.toString().split("").map(item => Number(item));
        const result = digits.reduce((accumulator, currentValue) => accumulator + currentValue,0);
        return result;
    }else{
        alert("the number is too big");
    }
}

에러 현상

테스트 실행 중, 런타임 에러가 발생했다.

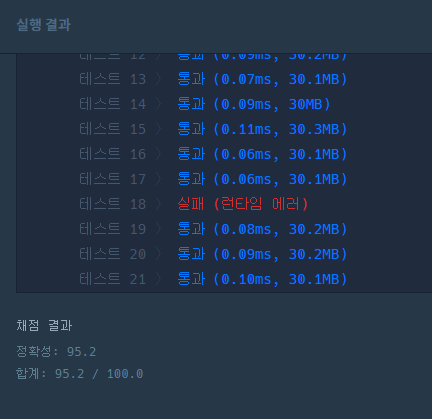
런타임 에러가 발생하는 주 요인은 다음과 같다.

1. 배열에 할당된 크기를 넘어서 접근했을 때 (배열 인덱스를 잘못 참조했을 때)
2. 전역 배열의 크기가 메모리 제한을 초과할 때
3. 지역 배열의 크기가 스택 크기 제한을 넘어갈 때
4. 0으로 나눌 떄
5. 라이브러리에서 예외를 발생시켰을 때
6. 재귀 호출이 너무 깊어질 때
7. 이미 해제된 메모리를 또 참조할 때

이 경우, 1번에 해당하는 에러가 발생한 것인데, 그 이유는 n 의 범위 설정을 잘못했기 때문이다.

...
    if(n<100_000_000){
      ...
    }
...

제한 사항에서, n 은 1억 미만의 자연수이다. 즉, 0 이하의 음수가 올 수는 없는 것이므로, 범위를 0<n<100_000_000 으로 설정해주어야 한다.

다른 방법

강사님처럼 do while 문을 사용하는 방법이 있는데, 이 방식이 속도가 더 빠르다고 한다.

references

Ha young, Kim

지적과 피드백은 언제나 환영합니다

자릿수 더하기

algorithm

자릿수 더하기

문제 설명

제한사항

문제 예시

keywords

문제 풀이

에러 현상

다른 방법

references

0개의 댓글