정렬 알고리즘이란?
원소들을 일정한 순서대로 열거하는 알고리즘 이다.
버블, 선택, 삽입, 합병, 힙, 퀵, 트리...
탐색 알고리즘이란?
선형, 이진, 해시...
Big-O
시간 복잡도 (소요되는 시간)
공간 복잡도 (메모리 사용량)
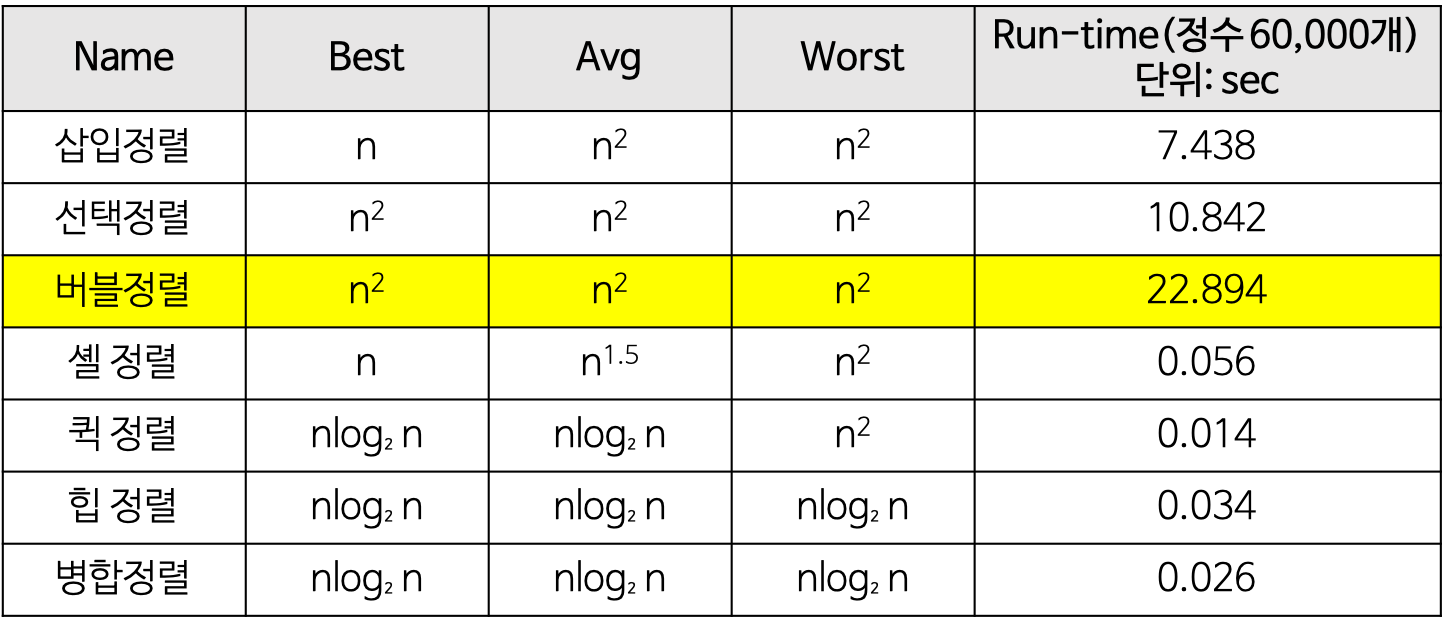
또한 정렬되는 항목 외에 충분히 무시할 만한 저장공간만을 더 사용하는 정렬 알고리즘들을 제자리 정렬이라고 한다.
swap()
두 인덱스의 원소 교환 메서드
public static void swap(int[] arr, int idx1, int idx2) {
int tmp = arr[idx1];
arr[idx1] = arr[idx2];
arr[idx2] = tmp;
}📍 정렬
1. 버블 정렬(Bubble Sort) 🐾
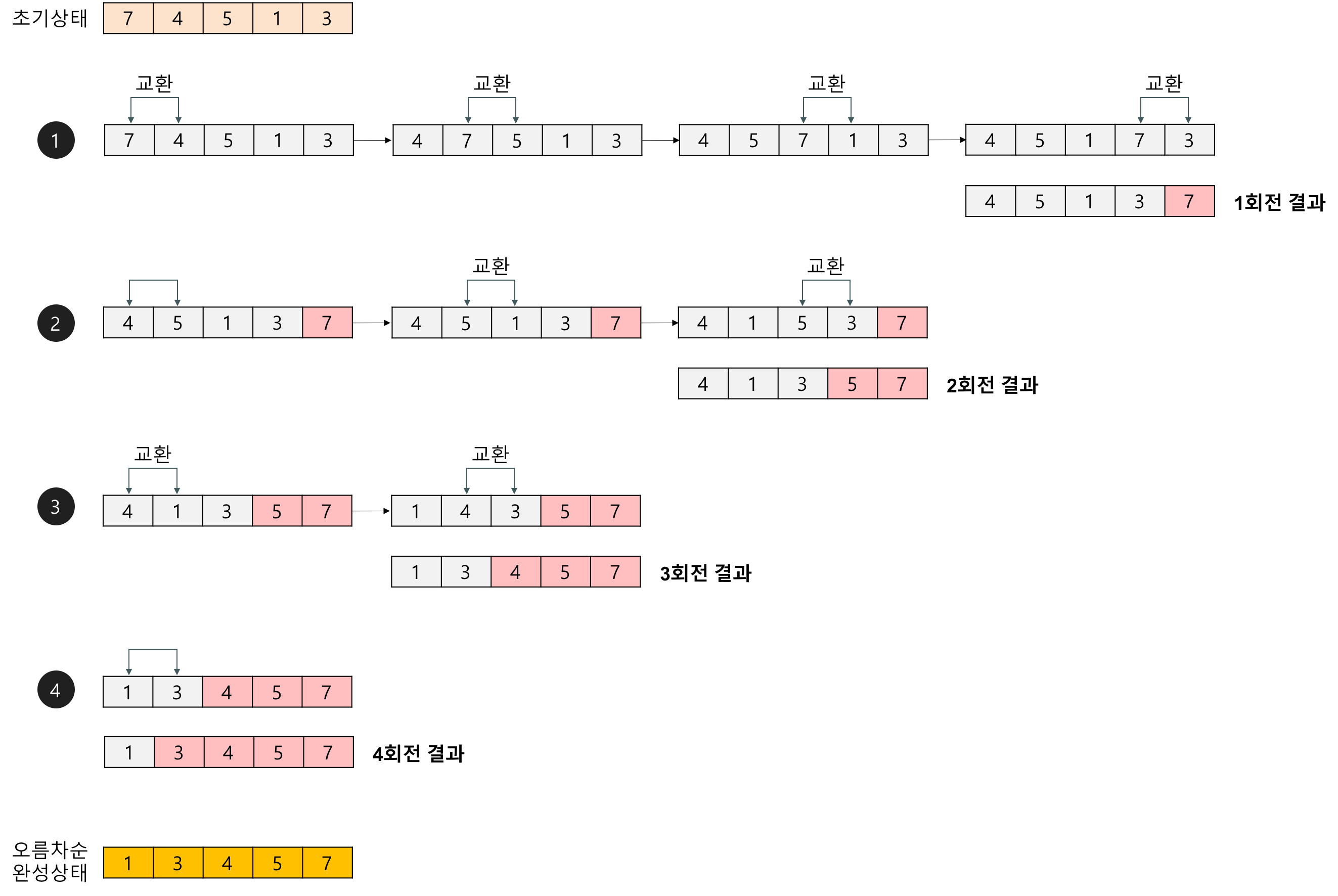
인접한 두 원소를 검사하여 정렬하는 알고리즘입니다.
버블 정렬이란 이름은 정렬과정이 거품처럼 위로 송송 올라오는 것과 유사하여 작명되었습니다.
버블 정렬 알고리즘은 설명과 구현이 가장 쉬운 알고리즘입니다.
비교와 교환이 모두 일어날 수 있기 때문에 코드는 단순하지만 성능은 좋지 않다.
* 선택 정렬과 기본 개념이 유사하다.
public static void sortByBubbleSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
}
}시간 복잡도
(정렬이 잘 되어있으면 n, 역으로 정렬되어있으면 n2)
worst: O(n^2)
average: O(n^2)
best: O(n^2)
장점
구현이 매우 간단하다.
단점
순서에 맞지 않은 요소를 인접한 요소와 교환한다.
하나의 요소가 가장 왼쪽에서 가장 오른쪽으로 이동하기 위해서는 배열에서 모든 다른 요소들과 교환되어야 한다.
특히 특정 요소가 최종 정렬 위치에 이미 있는 경우라도 교환되는 일이 일어난다.
2. 선택 정렬(Selection Sort)
맨 앞 인덱스부터 차례대로 들어갈 원소를 선택하여 정렬하는 알고리즘이다.
교환 횟수는 O(n)으로 적지만, 비교는 모두 진행된다.
한번 순회를 하면서 가장 큰 수를 찾아서 배열의 마지막 위치와 교환한다.
즉, 버블 정렬과 유사하나 보다는 성능이 좋다.
public static void sortBySelectionSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int minIdx = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[minIdx]) {
minIdx = j;
}
}
swap(arr, i, minIdx);
}
}시간 복잡도
worst: O(n^2)
average: O(n^2)
best: O(n^2)
3. 삽입 정렬(Insertion Sort)
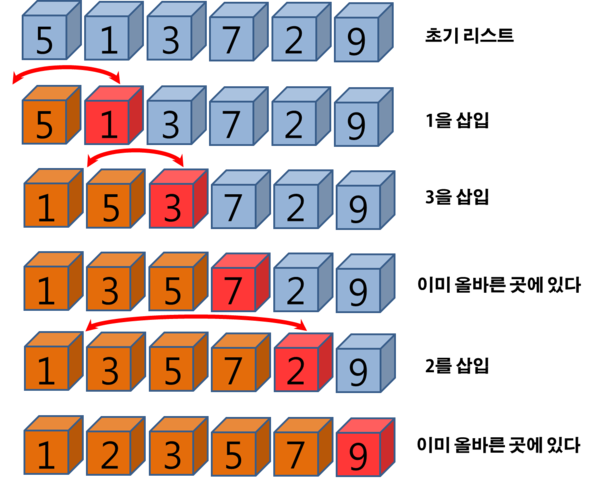
인덱스 1의 원소부터 앞 방향으로 들어갈 위치를 찾아 교환하는 정렬 알고리즘이다.
정렬이 되어 있는 배열의 경우 O(n)의 속도로 정렬되어 있을 수록 성능이 좋다.
코드 & 설명
public static void sortByInsertionSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int tmp = arr[i];
int j = i - 1;
while (j >= 0 && tmp < arr[j]) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = tmp;
}
}데이터가 쌓이는 과정
9
2 9
2 3 9
2 3 5 9
1 2 3 5 9
1 2 3 5 6 9
1 2 3 5 6 8 9
인덱스 1 ~ (n - 1) 의 원소들을 순차적으로 자신이 들어갈 위치에 넣는다.
while문을 사용하여 더 작으면 계속 앞으로 전진시키면서 비교한 원소를 한 칸씩 뒤로 민다.
들어갈 자리가 정해지면 넣어준다.
시간 복잡도
(버블정렬과 반대: 정렬이 잘 되어있으면 n2, 역으로 정렬된 상태라면 n)
worst: O(n^2)
average: O(n^2)
best: O(n)
4. 셸 정렬(Shell Sort)
삽입 정렬의 장점을 살리고 단점을 보완한 정렬 알고리즘이다.
삽입 정렬의 단점은 (n - 1)번째 인덱스 원소의 들어가야할 자리가 0번째 인덱스라면 많은 swap()을 해야하는 것이다.
단점을 보완하기 위하여 간격을 정하여 배열을 부분 배열들로 나누어 어느정도 정렬 시키고, 다시 간격을 줄여 정렬시키는 것을 반복한다.
여기의 영상을 한번 시청하면 이해가 빠를 것이다.
평균 시간 복잡도가 O(n^1.5)로 개선된다.
public static void sortByShellSort(int[] arr) {
for (int h = arr.length / 2; h > 0; h /= 2) {
for (int i = h; i < arr.length; i++) {
int tmp = arr[i];
int j = i - h;
while (j >= 0 && arr[j] > tmp) {
arr[j + h] = arr[j];
j -= h;
}
arr[j + h] = tmp;
}
}
}첫 번째 for문의 h는 간격을 의미한다. 간격이 배열의 길이의 반부터 1이 될때까지 for문을 돌린다.
두 번째 for문에서 부분 배열들을 삽입정렬 해준 뒤 모두 끝나면 간격을 반으로 줄인다.
간격이 1이 될 때까지 위 과정을 반복한다.
시간 복잡도
worst: O(n^2)
average: O(n^1.5)
best: O(n)
5. 합병(병합) 정렬(Merge Sort)
분할 정복 알고리즘 중 하나이다.
배열의 길이가 1이 될 때까지 2개의 부분 배열로 분할한다.
분할이 완료됐으면 다시 2개의 부분 배열을 합병하고 정렬한다.
모든 부분 배열이 합병될 때 까지 반복한다.
시간 복잡도가 O(nlog n)으로 빠르지만, 아래 코드를 보면 tmpArr을 사용해야 돼서 제자리 정렬보다 O(n)만큼 추가적인 메모리가 사용되는 단점이 있다.
보통은 재귀함수로 구현하므로 이 것또한 메모리를 많이 사용하게 된다.
코드 & 설명
public static void sortByMergeSort(int[] arr) {
int[] tmpArr = new int[arr.length];
mergeSort(arr, tmpArr, 0, arr.length - 1);
}
public static void mergeSort(int[] arr, int[] tmpArr, int left, int right) {
if (left < right) {
int m = left + (right - left) / 2;
mergeSort(arr, tmpArr, left, m);
mergeSort(arr, tmpArr, m + 1, right);
merge(arr, tmpArr, left, m, right);
}
}public static void merge(int[] arr, int[] tmpArr, int left, int mid, int right) {
for (int i = left; i <= right; i++) {
tmpArr[i] = arr[i];
}
int part1 = left;
int part2 = mid + 1;
int index = left;
while (part1 <= mid && part2 <= right) {
if (tmpArr[part1] <= tmpArr[part2]) {
arr[index] = tmpArr[part1];
part1++;
} else {
arr[index] = tmpArr[part2];
part2++;
}
index++;
}
for (int i = 0; i <= mid - part1; i++) {
arr[index + i] = tmpArr[part1 + i];
}
}재귀를 수행하는 부분인 mergeSort()와 재귀를 마치고 합병하는 부분인 merge()로 구성된다.
mergeSort()는 반으로 나누면서 재귀호출하며 다 나눠졌으면 점점 올라오면서 merge()한다.
merge()는 두 부분 배열의 인덱스를 점차적으로 비교하면서 정렬한다.
while문이 끝나고 배열에 좌측 부분배열의 남은 것만 저장하는 이유는 다음과 같다.
1. 우측 부분배열이 다 들어가고 좌측 부분배열만 남은 경우에는 좌측 부분 배열만 넣으면 됨.
2. 좌측 부분배열이 다 들어가고 우측 부분배열만 남은 경우에는 이미 배열은 다 정렬된 것.
2번이 이해가 잘 안될 수도 있는데, 정렬을 단계별로 그려보면 이해가 될 것이다.
시간 복잡도
worst: O(nlog n)
average: O(nlog n)
best: O(nlog n)
공간 복잡도
O(n)만큼의 추가 메모리 tmpArr 사용
6. 힙 정렬(Heap Sort)
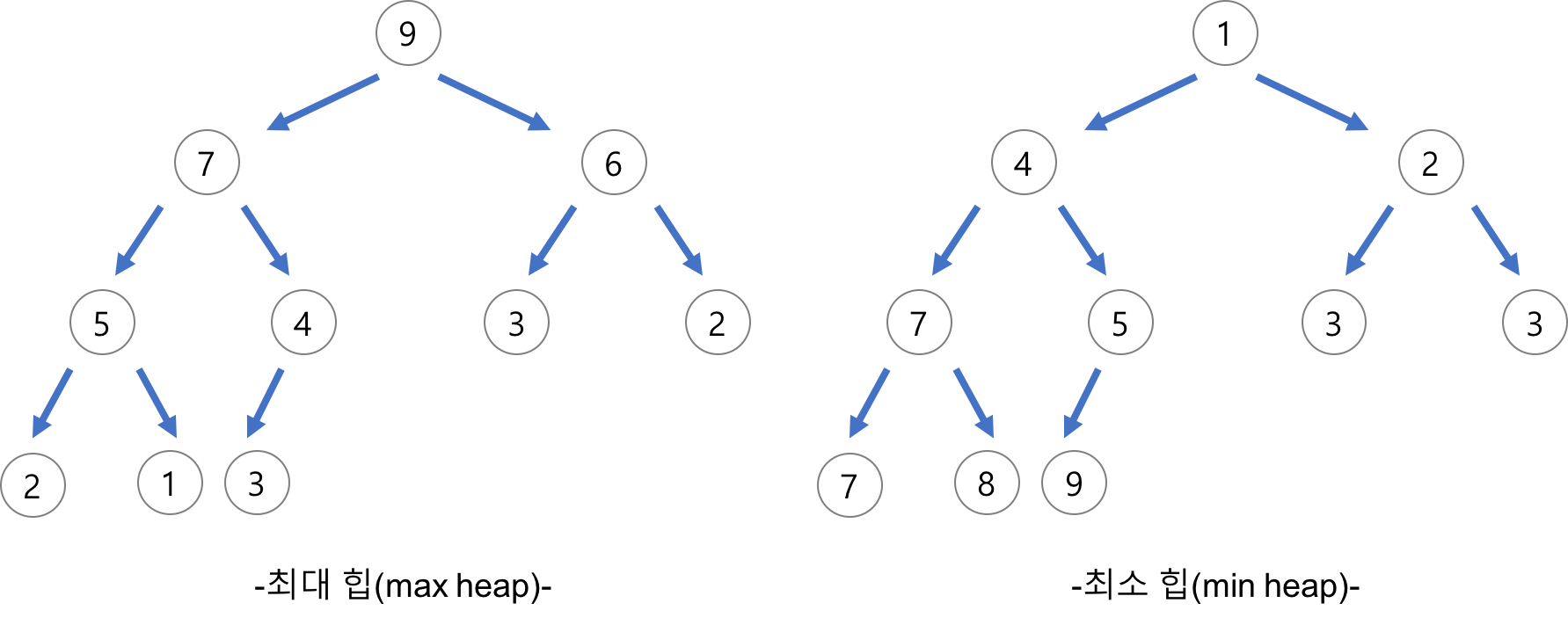
완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조
최댓값, 최솟값을 쉽게 추출할 수 있는 자료구조
https://gmlwjd9405.github.io/2018/05/10/algorithm-heap-sort.html
오름차 순 정렬일 때 최대힙을 사용하는 정렬이다. (내림차는 최소힙)
최대힙을 배열로 구현하면 0번째 인덱스가 가장 큰 수라는 점을 사용한다.
시간 복잡도가 O(nlog n)으로 합병정렬, 퀵정렬과 동일하지만 실상 성능은 더 낮게 나온다.
매번 루트에서 최대 값을 뺄 때마다 heapify()를 사용하여 다시 최대힙으로 만들어야 해서 그렇다.
필자가 구현한 코드로 볼 때는 메모리는 다른 두 정렬보다 적게 사용된다는 장점이 있다.
코드 & 설명
public static void sortByHeapSort(int[] arr) {
for (int i = arr.length / 2 - 1; i < arr.length; i++) {
heapify(arr, i, arr.length - 1);
}
for (int i = arr.length - 1; i >= 0; i--) {
swap(arr, 0, i);
heapify(arr, 0, i - 1);
}
}public static void heapify(int[] arr, int parentIdx, int lastIdx) {
int leftChildIdx;
int rightChildIdx;
int largestIdx;
while (parentIdx * 2 + 1 <= lastIdx) {
leftChildIdx = (parentIdx * 2) + 1;
rightChildIdx = (parentIdx * 2) + 2;
largestIdx = parentIdx;
if (arr[leftChildIdx] > arr[largestIdx]) {
largestIdx = leftChildIdx;
}
if (rightChildIdx <= lastIdx && arr[rightChildIdx] > arr[largestIdx]) {
largestIdx = rightChildIdx;
}
if (largestIdx != parentIdx) {
swap(arr, parentIdx, largestIdx);
parentIdx = largestIdx;
} else {
break;
}
}
}heapify()부터 설명하면, 배열, parentIdx, lastIdx가 주어지면 parentIdx를 알맞은 자리에 들어가게 하여 최대 힙을 만들어주는 함수이다.
어려울 것 없이 부모노드를 왼쪽 자식, 오른쪽 자식 중 존재하거나 더 큰 것과 비교하여 swap()하는 것을 반복하여 알맞은 자리로 보내주면 된다.
이제 로직을 설명하자면,
1. 배열을 최대 힙으로 만든다.
2. 배열의 0 번째 인덱스 원소(가장 큰 수)를 마지막 인덱스와 교환한다.
3. 0 번째 인덱스를 자기 자리로 보내주기 위하여 heapify()를 사용한다.
의 2번, 3번을 반복하면 되는데 반복하면서 마지막 인덱스를 1씩 감소시키면 된다.
시간 복잡도
worst: O(nlog n)
average: O(nlog n)
best: O(nlog n)
7. 퀵 정렬(Quick Sort)

- 재귀적
- 피벗(pivot)을 사용
- 불안정 정렬이며 (합병 정렬과 같은) 분할 정복 알고리즘
- 합병 정렬은 일정한 부분 리스트로 분할하지만 퀵 정렬은 피벗이 들어갈 위치에 따라 불균형하다.
장점
평균적으로 매우 빠른 수행 속도를 자랑
단점
- 합병 정렬과 속도가 비슷하고 힙 정렬보다 빠르지만, 최악의 경우 O(n^2)만큼 걸린다는 점, 보통 재귀로 구현하기 때문에 메모리를 더 사용할 수 있다는 단점
- 최악의 경우는 피봇을 최솟값이나 최댓값 으로 선택하여 부분 배열이 한쪽으로 계속 몰리는 경우이다.
코드 & 설명
public static void sortByQuickSort(int[] arr) {
quickSort(arr, 0, arr.length - 1);
}
public static void quickSort(int[] arr, int left, int right) {
int part = partition(arr, left, right);
if (left < part - 1) {
quickSort(arr, left, part - 1);
}
if (part < right) {
quickSort(arr, part, right);
}
}public static int partition(int[] arr, int left, int right) {
int pivot = arr[(left + right) / 2];
while (left <= right) {
while (arr[left] < pivot) {
left++;
}
while (arr[right] > pivot) {
right--;
}
if (left <= right) {
swap(arr, left, right);
left++;
right--;
}
}
return left;
}변수부터 설명하자면,
left는 부분 배열의 첫 인덱스, right는 부분 배열의 마지막 인덱스 이다.
pivot은 그 중간의 원소 값을 사용한다.
partition()에서
left의 원소 값이 pivot보다 클 때까지 증가 시키면서 찾는다.
right의 원소 값이 pivot보다 작을 때까지 감소 시키면서 찾는다.
둘다 찾았으면 두 원소를 교환한다.
반복하다 보면 자연스럽게 pivot 좌측에는 더 작은 값들이고 우측에는 더 큰 값들이다.
끝나면 pivot의 위치인 left를 반환한다.
그럼 전달 받은 pivot은 알맞은 위치에 특정 되었으므로 다시 pivot을 기준으로 좌측, 우측 부분집합으로 나누어 재귀 호출 한다.
시간 복잡도
worst: O(n^2)
average: O(nlog n)
best: O(nlog n)
📚 정렬 메서드
Arrays.sort()
배열을 오름차순으로 정렬
int[] numbers = {5, 2, 9, 1, 5, 6};
Arrays.sort(numbers);
System.out.println("오름차순 정렬:");
for (int num : numbers) {
System.out.print(num + " ");
}내림차순 정렬
Arrays.sort(numbers);
for (int i = 0; i < numbers.length / 2; i++) {
int temp = numbers[i];
numbers[i] = numbers[numbers.length - 1 - i];
numbers[numbers.length - 1 - i] = temp;
}
System.out.println("\n내림차순 정렬:");
for (int num : numbers) {
System.out.print(num + " ");
}📍 탐색
이진 검색 (바이너리 탐색)
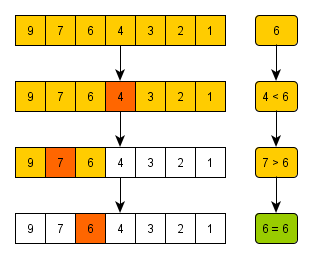
정렬되지 않는 리스트를 검색하려면 모든 원소를 찾기 위해 리스트를 모두 찾아야합니다.(완전탐색)
하지만 정렬된 리스트거나 검색하기 전에 정렬을 수행한 상황이라면 이진 탐색을 사용하는 것이 대표적입니다.
중간의 값을 설정하여 찾고자하는 데이터와 계속 비교해가며 범위를 축소해나가는 알고리즘입니다.
데이터가 많을 때 정말 효과적입니다. 백만 개의 원소가 있다면 20번 미만의 비교로도 주어진 원소를 찾을 수 있습니다.
시간 복잡도
성능은 O(log2n) 입니다.
References
