Shape As Points (SAP) 리뷰

1. Shape-As-Points (SAP): 새로운 3D 형상 표현 방식

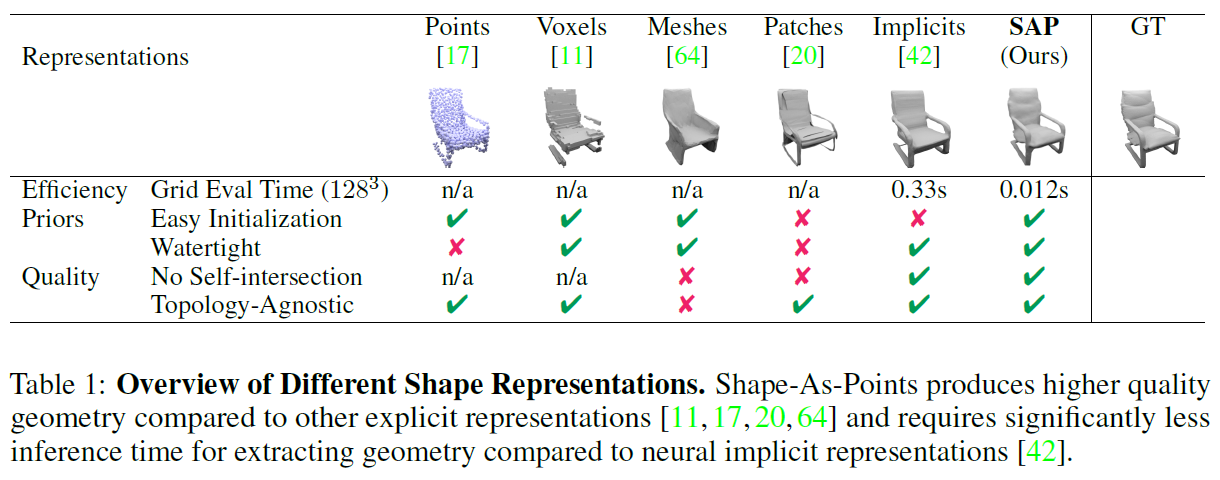
이 논문은 Shape-As-Points (SAP)라는 새로운 3D 형상 표현 방식을 소개하는 내용입니다. 주요 내용을 정리해 보겠습니다.

1.1. 배경 및 문제점

3D 컴퓨터 비전 및 그래픽스에서 형상 표현(Shape Representation)은 매우 중요합니다. 기존의 대표적인 방식들은 다음과 같은 특징과 한계를 가지고 있습니다.

포인트 클라우드(Point Cloud)

• 가볍고 쉽게 얻을 수 있지만, 표면(Surface) 정보를 직접적으로 인코딩하지 못함.

메시(Mesh)

• 일반적으로 고정된 위상(Topology)을 가져야 하므로 유연성이 부족함.

신경 암시적 표현(Neural Implicit Representation, NIR)

• 다양한 위상을 표현할 수 있고, 미분 가능한 구조와 쉽게 통합 가능하지만,
• 표면을 추출하려면 3D 공간에서 여러 번의 네트워크 평가가 필요해 속도가 느림.

1.2. SAP: Shape-As-Points (새로운 방법)

SAP는 GPU 가속 미분 가능한 푸아송 표면 재구성(Differentiable Poisson Surface Reconstruction, DPSR)을 활용하여 빠르게 3D 형상을 복원하는 방식입니다.

핵심 아이디어

• Poisson Solver를 활용해 점 클라우드에서 표면을 복원하는 지표 함수(Indicator Function)를 계산함.
• 기존 방식 대비 매우 빠르고 정확한 형상 복원이 가능함.
• 신경 암시적 표현보다 메모리 사용량이 적고, 빠르게 결과를 생성함.
• 노이즈가 있는 점 클라우드에서도 높은 성능을 발휘함.

1.3. SAP의 주요 장점

효율성(Efficiency)

• 기존 neural implicit network 방법(330ms)보다 훨씬 빠름 (128³ 해상도에서 12ms).
• 볼륨 데이터(예: Voxels)나 많은 네트워크 파라미터를 저장할 필요 없음.

정확성(Accuracy)

• 생성된 메시가 watertight 구조임 (물이 새지 않는 구조, 즉 빈틈이 없음).
• 자가 교차(self-intersection) 없음.
• 위상에 독립적(topology-agnostic).

초기화 용이성(Initialization)

• 템플릿 형상이나 노이즈가 많은 데이터에서도 쉽게 초기화 가능.
• 기존의 신경 암시적 표현보다 더 다양한 형상을 처리 가능.

1.4. 실험 및 성과

SAP는 기존 방법보다 연산 비용이 적으면서도, 노이즈가 있는 점 클라우드에서도 최상의 복원 성능을 보임.

• 학습이 필요 없는 최적화 기반 설정(Optimization-based setting)과
• 학습이 필요한 딥러닝 기반 설정(Learning-based setting) 모두에서 성능 검증됨.

1.5. 기여 내용 (논문의 핵심 주장)

✔ Shape-As-Points라는 새로운 형상 표현 방식을 제안.
✔ 빠르고 범용적인 미분 가능한 Poisson Solver를 설계.
✔ SAP의 속도, 초기화 용이성, 위상 독립성 등을 연구.
✔ 기존 방법 대비 더 낮은 연산 비용으로 더 높은 품질의 3D 복원 성능을 달성.

코드는 여기에서 제공됨:
코드 주소: Shape-As-Points GitHub Repository

---

2. Related Work

2.1 3D Shape Representations

3D 컴퓨터 비전 및 그래픽스에서 3D 형상 표현 방법은 크게 명시적(explicit) 표현과 암시적(implicit) 표현으로 나뉩니다.

명시적 표현 (Explicit Representations)

• 형상의 표면을 직접적으로 모델링.
• 대표적인 방법:
  • Point Cloud
  • 메시(Mesh)
  • 표면 패치(Surface Patches)
• 장점:
  • 간결하고 메모리 사용량이 적음.
• 단점:
  • Point-cloud, 표면 패치는 밀폐된(watertight) 표면을 만들기 어려움.
  • 메시 방식은 특정 형태(topology)에 제한됨.

암시적 표현 (Implicit Representations)

• 형상을 수학적 함수로 나타내는 방식.
• 대표적인 방법:
  • Voxel Grid 기반 표현
  • 신경망 기반(Neural Implicit Functions)
• 장점:
  • 부드러운 곡면 표현 가능.
• 단점:
  • 표면을 추출할 때 연산량이 많아 속도가 느림.

---

2.2 Optimization-based 3D Reconstruction from Point Clouds

Point-cloud에서 연속적인 표면을 복원하는 최적화 기반 방법들.

전통적인 방법

• Convex Hull, Alpha Shapes: 점을 감싸는 볼록 다각형 방식.
• Ball Pivoting Algorithm: 일정 반경의 구를 회전시켜 표면을 생성.
• Poisson Surface Reconstruction (PSR): 푸아송 방정식을 풀어 매끄러운 표면을 생성.
  • 단점: 입력 점의 법선(normals) 계산이 필요하여 노이즈에 취약.

신경망을 활용한 방법

• 신경망을 함수 근사자로 활용하여 표면을 학습.
• 단점: 높은 메모리 사용량과 연산 비용.

SAP 방법은 법선 추정 과정 없이 직접 복원 가능하며, 노이즈에 강함.

---

2.3 Learning-based 3D Reconstruction from Point Clouds

딥러닝을 활용한 3D 형상 복원 방법.

주요 접근법

• 국소 데이터 기반(Local Priors): 특정 부분의 형상을 예측 (대규모 형상 복원은 어려움).
• 객체 수준(Object-level) 및 장면 수준(Scene-level) 학습: 더 큰 스케일의 복원 가능.

전형적인 과정

1. 점 집합의 법선(normal)을 예측.
2. 예측된 법선을 활용해 Poisson Surface Reconstruction(PSR) 수행.

문제점:

• 노이즈가 많으면 법선이 부정확해져 복원이 실패할 가능성이 높음.

SAP 방법은 아웃라이어(outlier) 점을 자동으로 수정하거나 무시하는 기능을 갖추어 노이즈에 강함.

---

2.4 결론

• 기존 방법들은 표면 복원 품질과 연산 효율성 측면에서 한계를 가짐.
• 저자들의 방법은 법선 추정 없이도 강건한(watertight) 메쉬를 생성할 수 있어 더 효율적임.
• 특히, Poisson Equation을 활용하여 빠르게 계산 가능하다는 점이 특징.

---

3. Method (방법론)

3.1 미분 가능한 푸아송 해법 (Differentiable Poisson Solver)

• 푸아송 방정식(Poisson Equation)을 활용하여 3D 형상을 복원하는 방법.
• 입력 데이터:
  • $\mathbf{x} \in \mathbb{R}^3$ : 공간 좌표
  • $\mathbf{n} \in \mathbb{R}^3$ : 해당 좌표의 법선 벡터
• 핵심 개념:
  • 점과 법선 정보 $\{\mathbf{p} = (\mathbf{c}, \mathbf{n})\}$는 암시적(implicit) 형상 함수 $\chi(\mathbf{x})$의 그래디언트(gradient) 샘플로 볼 수 있음.
  • 이를 통해 형상을 정의하는 지시 함수(Indicator Function) $\chi(\mathbf{x})$를 계산 가능.
  • Indicator function의 그래디언트는 법선 벡터 필드와 연결됨.

---

3.1.1. 푸아송 방정식 변환 과정

1. Point-cloud 데이터로부터 법선 벡터 필드 $\mathbf{v(x)}$를 정의:

   $\mathbf{v(x)} = \sum_{(\mathbf{c_i, n_i}) \in \mathbf{P}} \delta(\mathbf{x - c_i, n_i})$
   $\delta(\mathbf{x, n}) = \begin{cases}\mathbf{n} & \text{if } x = 0 \\0 & \text{otherwise} \end{cases}$
   • 여기서 $\delta(\mathbf{x, n})$는 펄스 함수(Pulse Function)로 특정 위치에서만 값을 가짐.

2. 발산(divergence) 연산자를 적용하여 변형:

   $\nabla^2 \chi = \nabla \cdot \nabla \chi= \nabla \cdot \mathbf{v}$
   • 여기서 $\nabla^2$는 라플라시안 연산자(Laplacian Operator)이며, 위 식은 표준 푸아송 방정식이 됨.

3. 푸아송 방정식을 해석적으로 해결하기 위해 선형 시스템으로 변환:

   • 연속적인 방정식을 이산화(discretization)하여 격자(grid) 형태로 변환.
   • 결과적으로 발산 연산자의 역행렬을 계산하여 Indicator function을 구함.

Poisson 방정식의 수치적 풀이

• Poisson 방정식을 풀기 위해 함수 값과 미분 연산자를 이산화(Discretization)
• 균일한 샘플링 간격 $r$ 을 사용하여 격자(Grid) 생성
• $d = 3$ 인 경우, 격자의 크기는 $n := r \times r \times r = r^3$
• Poisson 방정식:
  $\nabla^2 \chi = \nabla \cdot \nabla \chi= \nabla \cdot \mathbf{v}$
  • $\chi$ 는 Indicator Function (표면을 나타내는 함수)
  • $\mathbf{v}$ 는 Point Normal Field (점에서의 법선 벡터 필드)

주요 연산자 정의

• Indicator Function $\chi$: 표면을 정의하는 함수, $\mathbb{R}^n$ 에서 정의
• Gradient Operator $\nabla$: $\mathbb{R}^n \to \mathbb{R}^{n \times d}$
• Divergence Operator $\nabla \cdot$: $\mathbb{R}^{n \times d} \to \mathbb{R}^n$
• Laplacian Operator $\nabla^2$: $\mathbb{R}^n \to \mathbb{R}^n$, 즉 $\nabla^2 = \nabla \cdot \nabla$
• 이를 활용하여 Poisson 방정식을 풀면 다음과 같은 형태로 변형됨:
  $\chi = (\nabla^2)^{-1} \nabla \cdot \mathbf{v}$
  • $(\nabla^2)^{-1}$: 라플라시안 연산자의 역연산
  • $\nabla \cdot \mathbf{v}$: 법선 벡터 필드의 발산

경계 조건 (Boundary Conditions)

Poisson 방정식을 풀 때는 추가적인 제약 조건 (Boundary Conditions) 이 필요함.
주어진 수식:

• s.t. (Subject To) → 다음과 같은 경계 조건을 만족해야 함
  1. $\chi |_{\mathbf{x \in \{c\}}} = 0$
     • 표면 점에서 $\chi$ 값은 항상 0이 되어야 함 (즉, 0 레벨 셋을 유지해야 함)
  2. $|\chi |_{x=0} = m$
     • 특정한 위치 $x = 0$ 에서 $\chi$ 의 크기를 $m = 0.5$ 로 고정
     • 전체 스케일을 조정하여 재구성된 표면의 크기를 일정하게 유지

4. 경계 조건(Boundary Condition) 설정
   • 표면 점에서 $\chi(x) = 0$이 되도록 함.
   • 전체 스케일을 $m = 0.5$ (at $x = 0$)로 고정하여 모호성을 제거.

정리

• 미분 가능한 푸아송 해법을 사용하여 Point-cloud데이터를 기반으로 형상을 복원.
• 푸아송 방정식을 활용해 Point-cloud으로부터 암시적 표면을 추정.
• 기존 Poisson Surface Reconstruction(PSR) 방법과 유사하지만, 미분 가능하게 설계하여 딥러닝 모델과 통합 가능.

---

3.1.2. Point Rasterization (포인트 래스터화)

목적

Point Cloud의 각 점에 대한 노멀 벡터(normal vector)를
Uniform Voxel Grid에 부드럽게 퍼뜨리기 (Rasterization).

이후 Poisson Surface Reconstruction (PSR)에 사용할 수 있도록
3D 공간에서 노멀 필드를 정의함.

입력 변수

• 점 데이터:
  $\mathbf{p}_i := (\mathbf{c}_i, \mathbf{n}_i)$

  • $\mathbf{c}_i = (x_i, y_i, z_i)$: 점 위치
  • $\mathbf{n}_i = (\hat{x}_i, \hat{y}_i, \hat{z}_i)$: 점 노멀 벡터

• voxel grid 정보:

  • $\mathbf{c}_0 = (x_0, y_0, z_0)$: voxel grid 시작 위치 (origin)
  • $s = (s_x, s_y, s_z)$: 각 voxel의 크기

주변 voxel index 찾기

점 $\mathbf{p}_i$는 위치상으로 주변 8개의 voxel vertex에 영향을 줌.

각 voxel 인덱스 $\mathbf{j} = (j_x, j_y, j_z)$는 다음처럼 계산됨:

여기서 $\lfloor\rfloor,\lceil\rceil$ 은 반올림에서 floor와 ceil operator입니다.
$j_y, j_z$ 도 같은 방식으로 계산

트릴리니어 보간 (trilinear interpolation) 가중치 함수

• $\mathcal{T}(\mathbf{c}_p, \mathbf{c}_v, \mathbf{s})$:
  점 $c_p$가 voxel vertex $c_v$에 주는 영향력 (가중치)
  → 가까울수록 더 크게, 멀수록 작게

개별 점이 voxel vertex에 주는 기여

• $\mathbf{s} \odot \mathbf{j} + \mathbf{c}_0$: 인덱스 $\mathbf{j}$에 해당하는 voxel vertex의 실제 3D 위치

모든 점의 기여를 합산

• $\mathcal{N}_j$: voxel vertex $j$ 근처에 있는 점들의 집합

정리

• 점의 노멀을 voxel vertex에 흩뿌릴 때 trilinear interpolation 사용
• 각 voxel vertex는 주변 점들의 영향을 가중합하여 벡터 필드 생성
• 이 벡터 필드는 PSR을 위한 입력값이 됨

---

3.1.3. 푸아송 방정식을 스펙트럴 도메인에서 풀기

변수 및 기호 정리

기호	의미
$\mathbf{v}$	점 노멀을 래스터화하여 만든 3D 벡터 필드 (공간 도메인)
$\tilde{\mathbf{v}} = FFT(\mathbf{v})$	벡터 필드 v의 푸리에 변환 (스펙트럴 도메인)
$\mathbf{u} = (u, v, w)$	푸리에 스펙트럼 상의 주파수 벡터 (x, y, z 방향 각각의 주파수)
$\|\mathbf{u}\|^2$	주파수 벡터의 L2 노름 제곱 ($i.e., u^2 + v^2 + w^2$)
$i$	허수 단위 (imaginary unit)
$\odot$	원소별 곱 (element-wise product)
$\tilde{g}_{\sigma, r}(\mathbf{u})$	가우시안 필터 (스펙트럴 도메인에서 smoothing 용도)

주 수식

이 수식은 푸아송 방정식을 푸리에 도메인에서 푸는 일반적인 형태입니다.

주 수식 상세 설명

푸아송 방정식은 보통 이렇게 생겼습니다:

• $\chi$: 우리가 구하고 싶은 스칼라 필드 (여기서는 물체의 내부를 나타내는 indicator function)
• $\mathbf{v}$: 벡터 필드 (노멀 정보에서 만들어짐)

푸리에 도메인에서 라플라시안($\nabla^2$)은 다음과 같이 작용합니다:

그리고 divergence($\nabla \cdot \mathbf{v}$)는 푸리에 공간에서는:

따라서 전체를 정리하면:

이 공식은 주 수식 구조와 거의 동일하며, 다만 논문에서는 이 결과에 가우시안 필터를 곱해서 Gibbs 현상 완화를 추가하고 있습니다.
(논문의 주 수식에서 $4\pi$ 대신에 $2\pi$을 나누었고, Gaussian smoothing 커널을 도입했습니다.)

Gaussian Kernel

• 여기서 $\sigma$는 가우시안의 스무딩 정도를 조절하는 하이퍼파라미터
• $r$은 격자의 해상도
• 이 필터는 고주파 성분을 감쇠시켜 ringing 현상을 줄입니다

공간 도메인으로 복원

위의 결과 $\tilde{\chi}$ 를 역 푸리에 변환하면:

이는 아직 스케일 조정과 평균 보정이 되지 않은 초기 형태의 indicator function입니다.

최종 결과 만들기

해석:

• $\mathbf{c}$는 입력 포인트 클라우드의 점들
• $\chi'|_{\mathbf{x=c}}$: 점 $\mathbf{c}$ 위치에서의 indicator 값

---

3.2 SAP for Optimization-based 3D Reconstruction 정리

Shape as Points (SAP) 논문에서 제안하는 최적화 기반 3D 복원 기법에 대해 설명드립니다. 특히, 비정렬된 포인트 클라우드(unoriented point clouds)로부터 3D 표면(mesh)을 복원하는 전체 파이프라인을 소개합니다.

핵심 아이디어 요약

• SAP는 미분 가능한 Poisson Solver를 사용하여 3D 포인트 클라우드에서 메쉬를 생성합니다.
• 기존의 latent code를 업데이트하는 방식이 아닌, 입력 포인트 자체를 직접 최적화합니다.
• 전체 과정은 forward → loss 계산 → backward → resampling → coarse-to-fine 최적화로 구성됩니다.

파이프라인 구성 단계

3.2.1. Forward Pass

• 입력 초기화: 보통은 입력 포인트 + 추정된 노멀(normals)을 사용하지만, SAP는 일반 구(sphere, 반지름 r)로 시작하여 모델의 일반성과 강건함을 테스트합니다.
• 초기 포인트 클라우드에 Poisson Solver를 적용해 indicator function 그리드를 생성합니다.
• Marching Cubes 알고리즘을 통해 indicator function을 메쉬로 변환합니다.

3.2.2. Backward Pass (손실 계산 및 역전파)

• 메쉬 표면$\mathcal{M}$에서 점 $\mathbf{p}_{mesh}$를 샘플링하고, 입력 포인트 클라우드와의 Chamfer Distance ($L_2$ 거리)를 계산합니다.
• 역전파 시, 다음과 같이 체인 룰을 사용하여 gradient를 분해합니다:

• 여기서 $\chi$는 indicator function이며, 중간 항 $\frac{\partial \mathbf{p}_{\text{mesh}}}{\partial \chi}$는 미분 불가능하지만 다음과 같이 근사할 수 있습니다:

• ($\mathbf{n}_{\text{mesh}}$는 해당 메쉬 점의 노멀 벡터입니다.)

3.2.3. Resampling (포인트 재샘플링)

• 최적화 중 포인트가 드리프트하거나 이상치가 생길 수 있기 때문에, 200번의 iteration마다 가장 큰 메쉬 컴포넌트에서 포인트와 노멀을 재샘플링합니다.
• 이를 통해 더 균일한 분포와 강건한 최적화가 가능합니다.

3.2.4. Coarse-to-Fine 전략

• 초기부터 고해상도로 시작하면 느리기 때문에, 점진적으로 해상도를 높이는 방식을 사용합니다:

단계	해상도	반복 횟수
초기	32³	1000
중간	64³	1000
...	...	...
최종	256³	-

• 각 단계에서 coarse한 메쉬를 얻고, 이를 기반으로 refinement를 반복합니다.

3.2.5. 비교 포인트

기존 방법 (ex. MeshSDF)	SAP 방식
학습된 shape latent vector 업데이트	입력 포인트 자체를 직접 업데이트
SDF 기반 암묵적 표현	Poisson 기반 indicator function 사용
Backprop 어려움	Gradient 근사 및 직접 전달 가능

---

3.3 SAP for Learning-based 3D Reconstruction 설명

핵심 개요

이 섹션은 SAP(Shape as Points)를 딥러닝 기반 3D 복원 문제에 적용하는 방법을 설명합니다.
즉, 조건부 모델을 학습하여 noisy하고 방향이 없는(unoriented) 포인트 클라우드로부터 watertight 메쉬를 예측하는 구조입니다.

주요 구성 요소 및 흐름

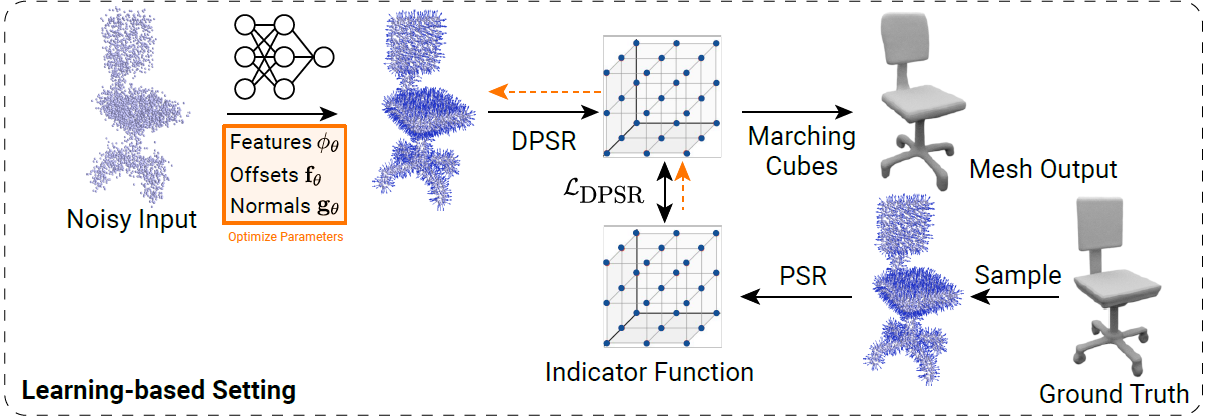
3.3.1. 입력: 노이즈 있는 unoriented point cloud

• 입력은 노이즈가 있는 포인트 클라우드로, 방향(노멀)이 없습니다.
• 모델의 목적은 이를 정확한 위치 + 방향(normals)을 가진 point cloud로 복원하는 것입니다.

3.3.2. 특징 추출 (Feature Encoding)

• 입력 포인트 클라우드를 ConvOnet의 point convolution 인코더를 사용하여 특징 벡터 $\phi_{\theta}(\mathbf{c})$로 변환합니다.
• 이 특징은 각 포인트의 지역(local) 정보와 전역(global) 정보를 모두 포함합니다.

3.3.3. Offset 예측 Multi Layer Perceptron (MLP) $f_\theta$

• 포인트 위치 $\mathbf{c}$와 그 특징 $\phi_{\theta}(\mathbf{c})$를 입력으로 받아 위치 보정 offset $\Delta \mathbf{c}$를 예측:

• $k$개의 offset을 예측하여 포인트 클라우드를 더 촘촘하게(densify) 만듭니다.

• 실험에서는 $k = 7$을 사용합니다.

3.3.4. Normal 예측 (MLP $g_\theta$)

• 보정된 포인트 $\hat{\mathbf{c}}$에 대해 또 다른 MLP로 노멀 $\hat{\mathbf{n}}$을 예측:

3.3.5. Poisson Solver + Loss

• 예측한 포인트와 노멀을 미분 가능한 Poisson Solver (DPSR)에 넣어 indicator grid $\hat{\chi}$를 생성합니다.
• Ground truth는 watertight mesh에서 point cloud를 샘플링해서 만든 grid $\chi$입니다.
• 두 grid 간의 MSE (Mean Squared Error)를 loss로 계산합니다:

학습 및 추론 (Training & Inference)

• 학습: 예측 포인트 → DPSR → $\hat{\chi}$ → MSE loss 계산
• 추론: 입력 포인트 클라우드 → offset 포인트 + 법선 예측 → DPSR → Marching Cubes → 메쉬 추출

네트워크 구조 요약

• MLP $f_\theta$, $g_\theta$: 각각 5개의 ResNet block으로 구성
• hidden dimention: 32
• 두 $MLP$는 파라미터를 공유하지 않음
• Optimizer: Adam, learning rate = $5 \times 10^{-4}$
• 프레임워크: PyTorch 사용

3.3.6. 체인 룰을 이용한 Gradient 계산

우리가 원하는 건:

즉, 파라미터 $\theta$ (여기선 $f_\theta$, $g_\theta$의 파라미터)에 대한 loss의 gradient입니다.

이걸 체인 룰로 전개하면:

여기서 각 항목을 보면:

• $\frac{\partial L}{\partial \hat{\phi}} = 2 (\hat{\phi} - \phi)$
  → MSE loss의 gradient
• $\frac{\partial \hat{\chi}}{\partial \hat{c}}, \frac{\partial \hat{\chi}}{\partial \hat{n}}$
  → DPSR이 differentiable Poisson solver이므로 자동미분 가능
• $\frac{\partial \hat{c}}{\partial \theta}$, $\frac{\partial \hat{n}}{\partial \theta}$
  → 각각 offset MLP와 normal MLP의 미분

PyTorch에서는 이 전체 파이프라인을 computational graph로 만들어 놓으면, .backward() 호출 시 자동으로 이 전체 체인 룰을 따라 gradient를 계산해줍니다.

정리

• DPSR은 differentiable이기 때문에 $\hat{c}, \hat{n}$에 대해 gradient를 전달 가능
• $\hat{c}, \hat{n}$은 각각 $f_\theta, g_\theta$를 통해 예측되므로
  최종적으로 loss는 $\theta$에 대해 체인 룰을 따라 미분 가능
• 전체 loss gradient:

---

4장. 실험 결과

이 장은 제안한 3D 재구성 기법의 성능을 다양한 조건에서 테스트한 실험 결과를 설명합니다.
논문에 제안한 방법을 검증하기 위해 다음 두 가지 실험을 수행했습니다:

1. 최적화 기반 3D 재구 (Optimization-based 3D Reconstruction)
   → 방향 정보가 없는 포인트 클라우드에서 하나의 객체의 표면을 재구성합니다.

2. 학습 기반 재구성 (Learning-Based Surface Reconstruction)
   → ShapeNet 데이터셋의 노이즈 포함 포인트 클라우드를 이용해 표면 재구성을 수행합니다. 일부 실험에서는 이상치(outliers)도 포함됩니다.

---

4.1 최적화 기반 3D 재구성 (Optimization-based 3D Reconstruction)

입력 데이터 종류

1. 합성 메시에서 샘플링한 포인트 클라우드 (가우시안 노이즈 포함)
2. 실제 스캔 데이터
3. 고해상도 인간 스캔 데이터 (노이즈가 적음)

실험 결과 요약

• 제안 방법이 기존 방법들보다 뛰어난 성능을 보였습니다.
• 복잡한 형상, 얇은 구조물, 결손이 많은 관측 등 어려운 조건에서도 강건한 재구성 가능했습니다.

기존 기술과 논문 제안 방법 비교

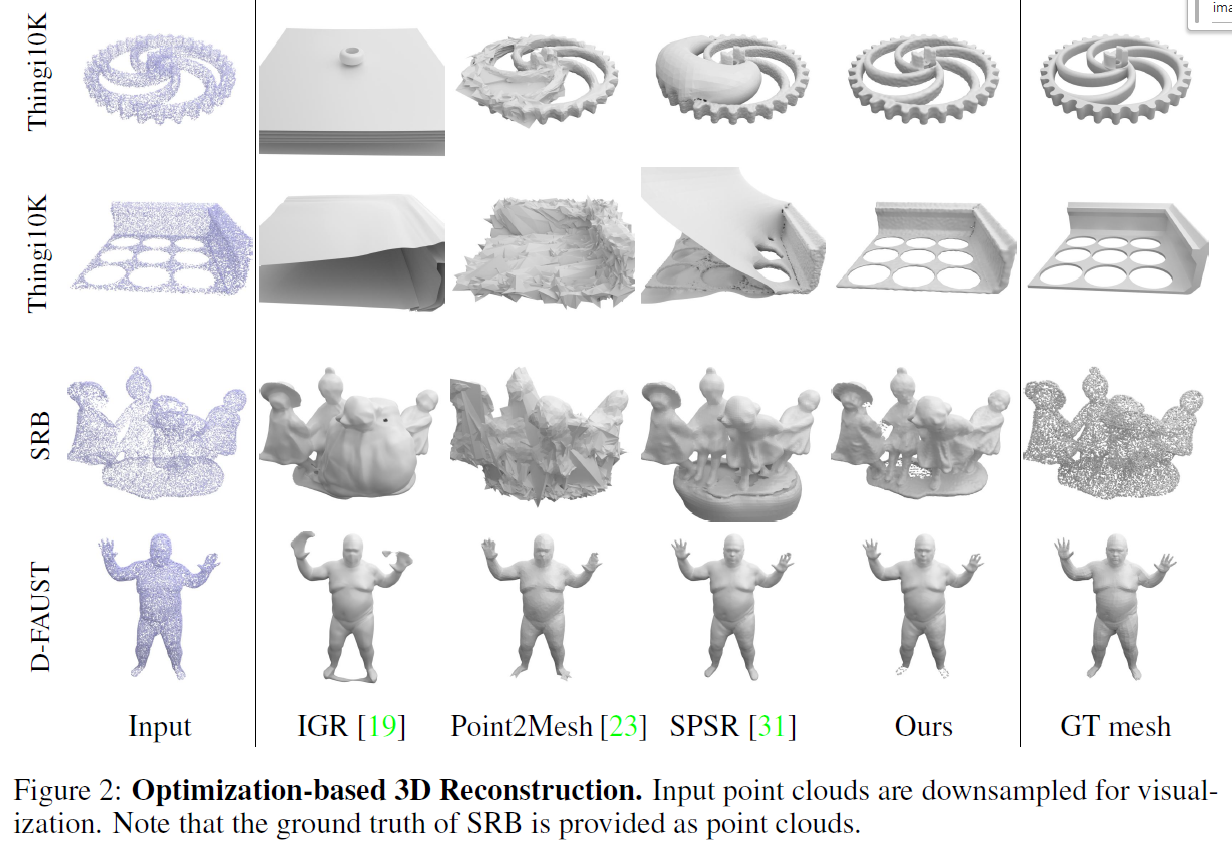
기술명	설명 및 한계점
IGR	방향 정보가 없는 포인트 클라우드에 대해, 메시가 허공에 생성되는 문제가 있음
Point2Mesh	Chamfer distance로 최적화하지만, 초기 메시 필요 및 위상 고정이라는 제약 존재. 초기 메시 생성은 SPSR에 의존
SPSR	속도는 빠르지만, 노이즈 있는 데이터에서 법선 추정이 부정확함
제안 방법	초기 메시 없이 Chamfer distance 기반 최적화. 점과 법선을 동시에 최적화하여 robust한 성능 달성. 수렴 속도도 빠름

한계점

• 관측되지 않은 영역(예: 발바닥)은 복원이 되지 않음
  → 이는 이후의 학습 기반 재구성으로 보완 가능

추가 실험: 노이즈 및 이상치 포함

ShapeNet 데이터셋을 이용하여, 다음과 같은 노이즈 조건에서 제안 방법의 성능을 평가합니다:

1. 작은 노이즈: 평균 0, 표준편차 0.005의 가우시안 노이즈
2. 큰 노이즈: 평균 0, 표준편차 0.025의 가우시안 노이즈
3. 혼합 노이즈 + 이상치:
   • 50%: 조건 ①과 동일한 노이즈
   • 50%: 단위 큐브 내 균일 분포로 샘플링된 이상치 포인트

이 실험은 제안한 미분 가능한 Poisson 솔버(differentiable Poisson solver) 가 학습 기반 재구성에서도 유용한지를 검증합니다.

4.2 학습 기반 재구성 (Learning-based Reconstruction on ShapeNet)

성능 비교 결과

• 그림 3(Fig. 3)과 표 3(Table 3)에서 실험 결과가 제시됩니다.
• 제안한 방법은 기존 기법들과 비교하여 모든 평가 지표에서 유사하거나 더 나은 성능을 보입니다.

핵심 포인트

• 기존 방식:
  • Chamfer loss: 점 위치 차이
  • L1 loss: 법선 벡터 차이
• 제안 방식:
  • DPSR loss (Differentiable Poisson Surface Reconstruction loss) 사용
  • 표면을 간접적으로 정의하는 indicator grid를 직접 감독함으로써 더 나은 재구성 성능 달성

기존 기술의 한계

• SPSR은 노이즈나 이상치(outliers)에 매우 취약
• 포인트 클라우드, 메시, 복셀 그리드, 패치 기반 방법보다 일관되게 더 나은 성능
• 이상치(outliers)에 대해서도 제안 기법이 강건함(robustness)을 보임

실행 속도 비교 (Runtime)

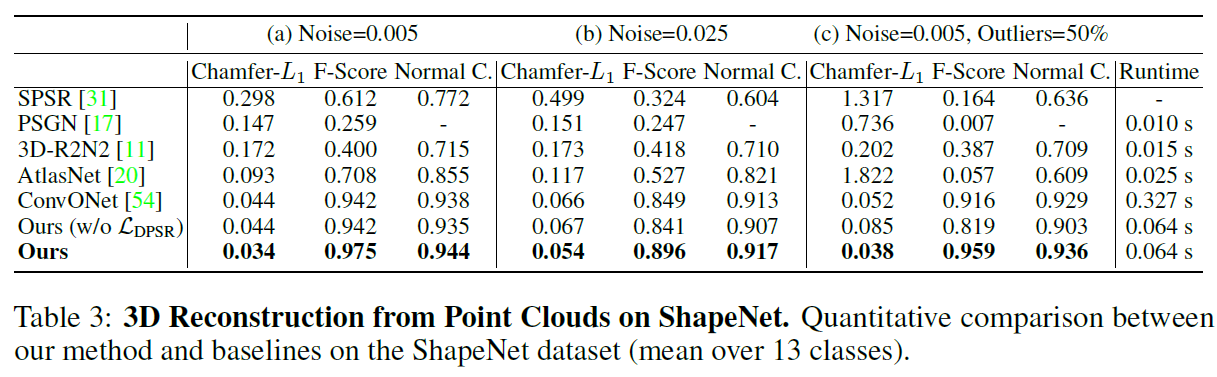
• 표 3(Table 3)에는 다양한 GPU 가속 기법들의 실행 시간도 포함됨
• 실험 환경: NVIDIA GTX 1080Ti GPU, ShapeNet 테스트셋 전체 평균 기준

주요 결과 요약

방법	품질	속도
기존 기술	낮음	빠름
Neural implicit model	높음	느림
제안 기법	높음	적당히 빠름 (균형 잡힘)

---

ConvONet과의 세부 비교

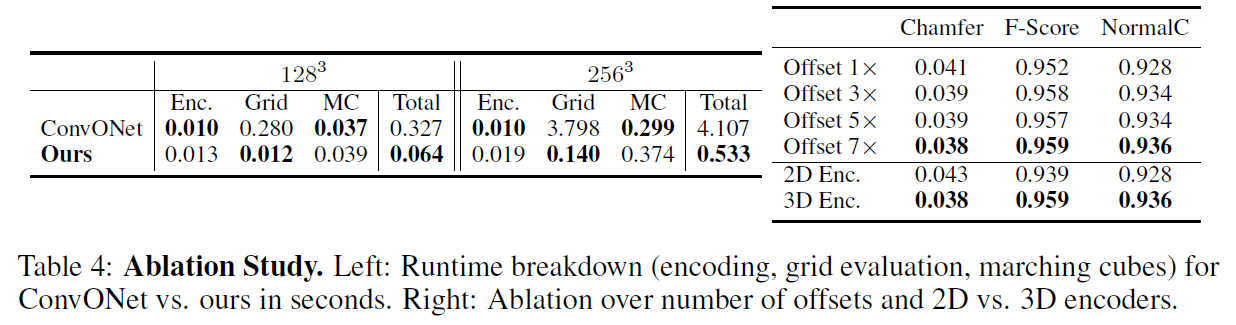
• 제안 기법과 ConvONet은 비슷한 재구성 파이프라인을 공유
• 따라서 해상도 128³, 256³에서의 처리 속도 및 세부 처리 단계 비교 (표 4 참고)

처리 시간 구성요소별 차이

• 포인트 인코딩과 Marching Cubes는 시간 차이 거의 없음
• Indicator Grid 연산에서는 제안 기법이 ConvONet보다 20배 이상 빠름

전체 추론 시간 기준

• 128³ 해상도: 약 5배 빠름
• 256³ 해상도: 약 8배 빠름

---

4.3 제거 연구 (Ablation Study)

ShapeNet의 가장 어려운 조건(세 번째 설정)에서 아키텍처 구성 요소의 영향을 실험적으로 분석

1. Offset 수 (Number of Offsets)

• 입력 포인트당 더 많은 offset을 예측할수록 성능 향상
• 이유: 객체 표면 근처의 포인트 수가 많아져 기하학적 디테일 보존에 유리

2. 포인트 클라우드 인코더 (Point Cloud Encoder)

• 비교 대상:

  1. 2D 인코더: 세 개의 기준 평면(64² 해상도)에 투영
  2. 3D 인코더: 3D 특징 볼륨 기반 (해상도 32³)

• 결과: 3D 인코더가 더 우수

• 이유 추정: 3D indicator grid와의 표현 정렬(alignment)이 뛰어남

---

5. 결론 (Conclusion)

이 논문은 Shape-As-Points (SAP) 라는 새로운 형상 표현 방식을 소개했습니다. 이 방식은 다음과 같은 특징을 가집니다:

• 경량(Lightweight)
• 해석 가능성(Interpretable)
• 효율적으로 수밀한(watertight) 메시 생성 가능

우리는 방향 정보가 없는 포인트 클라우드로부터의 표면 재구성(surface reconstruction) 작업에서,
최적화 기반과 학습 기반 두 가지 설정 모두에서 이 방법의 효과를 입증했습니다.

한계점

우리 방법은 지표 그리드(indicator grid) 해상도에 따라 메모리 요구량이 세제곱으로 증가하기 때문에,
현재는 작은 장면(small scenes)에만 적용이 가능합니다.

향후 확장 가능성

이 문제를 해결하기 위해 다음과 같은 방식을 고려할 수 있습니다:

• 슬라이딩 윈도우(sliding-window) 방식으로 장면을 나누어 처리
• 옥트리(octree) 등의 공간 적응형 자료 구조(space-adaptive data structures) 활용

이를 통해 더 큰 장면에도 본 방법을 확장할 수 있을 것으로 기대됩니다.

영향

포인트 클라우드 기반 기법들은 다음과 같은 실제 응용 분야에서 널리 사용됩니다:

• 가정용 로봇
• 자율주행 자동차

따라서 본 방법 역시 다른 학습 기반 3D 재구성 기술들과 동일한 사회적 기회와 위험성을 공유합니다.