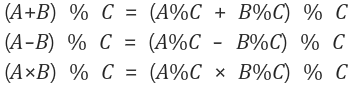곱셈 - 1629번

문제

자연수 A를 B번 곱한 수를 알고 싶다. 단 구하려는 수가 매우 커질 수 있으므로 이를 C로 나눈 나머지를 구하는 프로그램을 작성하시오.

입력
첫째 줄에 A, B, C가 빈 칸을 사이에 두고 순서대로 주어진다. A, B, C는 모두 2,147,483,647 이하의 자연수이다.

출력
첫째 줄에 A를 B번 곱한 수를 C로 나눈 나머지를 출력한다.

풀이

너무 간단한 산수 문제라 처음에 당황했다. 당연히 아래의 답안으로 제출했고, 당연히 시간초과가 떴다. 아래는 통과하지 못하는 코드이다.

import sys 
input = sys.stdin.readline
A, B, C = input().split()
A = int(A)
B = int(B)
C = int(C)

print((int(A)**int(B))%int(C)) # 시간초과

문제는 매우 큰 수가 들어오면 0.5 초 (추가 시간 없음)라는 시간제한에 칼같이 걸러버린다. 자고로 파이썬에서는 수가 커지면 곱셈에 걸리는 시간도 그만큼 오래 걸린다. 정답 비율 26%대네...
그래서 이 문제는 반드시 분할하여 재귀함수를 통해 접근하는 풀이법으로 풀어야 통과시켜준다.

분할정복 기법은 예를 들자면, 2^32의 계산을 2^16x2^16 으로, 2^16에 대해서는 2^8x2^8 으로 점차적인 문제의 분할을 해가며 전체 문제풀이에 접근하는 방식이다.

위 한 문장만 딱 봐도 재귀각이라는 느낌이 든다! 문제의 핵심을 들여다 보면 "자연수 A에 대한 B제곱"의 B를 계속해서 2분할, 또 2분할, 또 2분할하여 B가 더 이상 2로 나눌 수 없는 자연수인 1이 될 때까지 재귀 호출을 하도록 하면 된단 점일 것이다.

벌써 우리의 함수가 가질 탈출문의 조건이 나왔다. b==1일 때 우린 재귀 호출을 멈춘다.

우리의 함수를 def dac(a, b, c) 라고 했을 때, 이를 전형적인 재귀함수를 설명할 때 쓰는 recur(N)라고 가정하자.
그렇다면 recur(N)을 호출할 recur(N-1)은, 우리의 함수로 치면 아마 dac(a, b//2, c)이 될 거다.

다만 중요한 것은 2^32의 계산을 2^16x2^16 으로 나누듯 우리의 식 속 B는 재귀적으로 호출되면서 홀수이기도 짝수이기도 해가며 변할 거고, 이는 언제나 깔끔하게 2분할될 보장이 없다. 인자 b가 호출마다 홀수 짝수인 경우를 나누어 처리하도록 수식을 작성한다.

아래의 코드는 정답이다.

import sys 
input = sys.stdin.readline
A, B, C = input().split()
A = int(A)
B = int(B)
C = int(C)

def dac(a, b, c):
  if b==1:
      return a%c
  else:
      tmp = dac(a, b//2, c)
      if b%2==0:
          return (tmp * tmp) % c
      else:
          return (tmp * tmp * a) % c

print(dac(A, B, C))

일단 코드를 본 뒤, 의문이 생길 수도 있다. 아마 높은 확률로 그건 중고등학교 때 배운 나머지 분배 법칙을 까먹고 있어서 일 거다. (나도)

나머지 분배 법칙
(a + b)%c = (a%c + b%c)%c
(a x b)%c = (a%c x b%c)%c

코드의 예시를 들자면, ( dp[i] + dp[j] ) % C = ( dp[i]%C + dp[j]%C ) %C 인 것.

알고리즘 문제를 푸는 과정에서 결과 값이 매우 큰 경우, 결과 값의 나머지를 구하라는 문제가 자주 등장한다.
단순히 결과 값에 모듈러 연산을 수행할 시 이미 결과 값은 너무 커져서 오버플로우가 발생한 경우가 대부분이기 때문에, 연산 과정 도중에 모듈러 연산을 적용해야 한다.

연산 과정 도중에 모듈러 연산을 적용하려면 모듈러 연산의 분배법칙에 대해 알아야 한다.

각 피연산자에 모듈러 연산을 취한 후, 계산 결과에 대해 다시 한 번 모듈러 연산을 취하면 된다.
이때, 뺄셈의 경우 음수가 나오는 것을 방지하기 위해 divisor를 한 번 더해준다고 한다.

아래 블로그가 좋은 참고가 됐다.
https://velog.io/@sw801733/%EB%82%98%EB%A8%B8%EC%A7%80-%EC%97%B0%EC%82%B0-%EB%B6%84%EB%B0%B0%EB%B2%95%EC%B9%99-%EB%AA%A8%EB%93%88%EB%9F%AC-%EC%97%B0%EC%82%B0

그래서...
우리가 작성한 함수는 계속해서 a%c를 재귀적으로 호출하며 전체 수식을 만들어 내는 것이고, 다만 b가 홀수인 호출에서만 따로 a를 한 번 더 곱해준다. B==11이라는 예제 안에서 대강 함수가 재귀적 호출되는 형태는 이런 식으로 보여진다.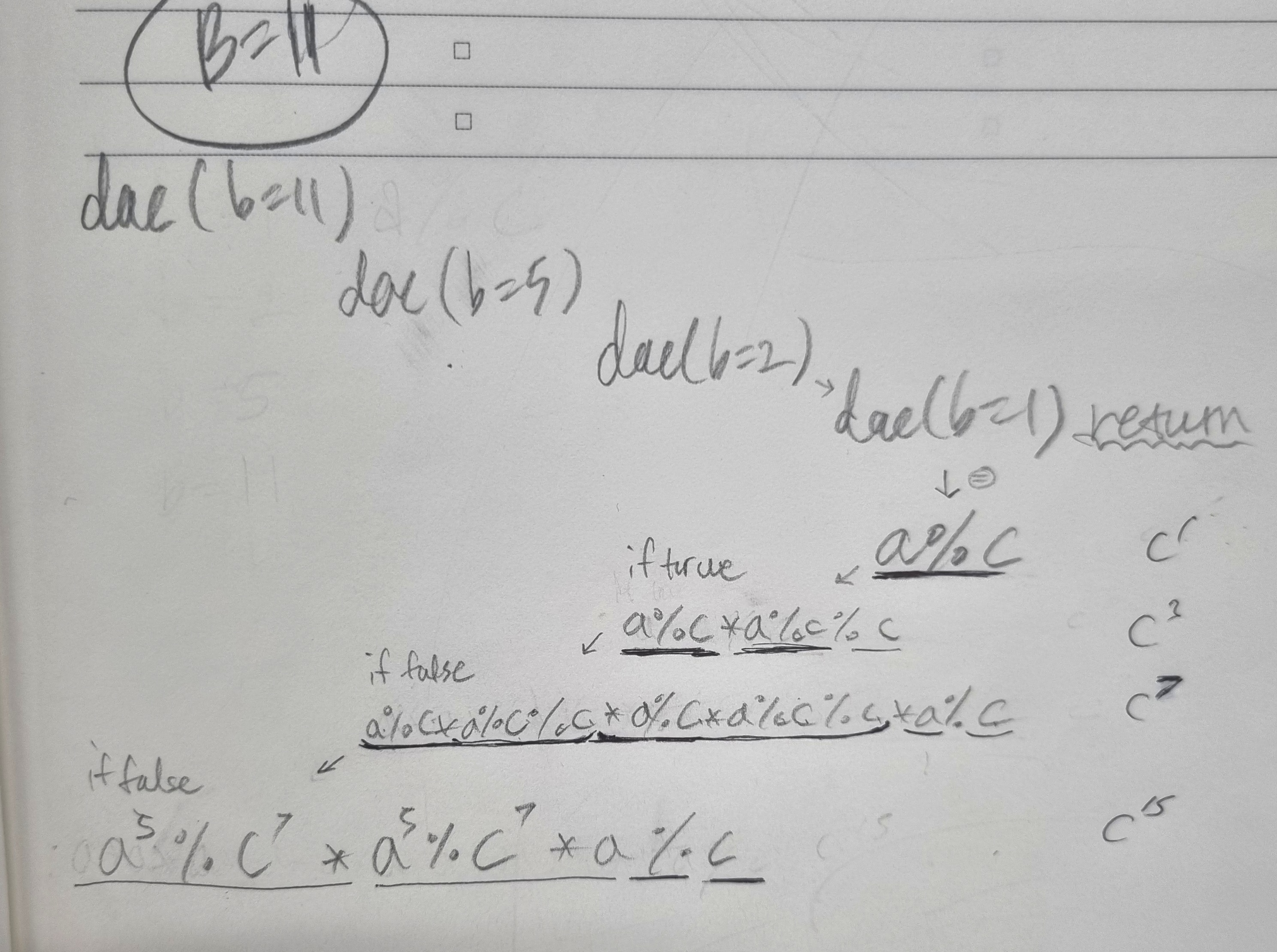

참고로 여기서 %C가 많이 호출되는 점에 의문이 생겼었는데, 이는 어차피 나머지를 리턴하므로 몇 번을 거듭하여 나누어도 결과가 똑같다는 점에서 아무 상관이 없단 걸 깨달았다. 형인님 고마워용~