사냥꾼 - 8983번

문제

KOI 사냥터에는 N 마리의 동물들이 각각 특정한 위치에 살고 있다. 사냥터에 온 사냥꾼은 일직선 상에 위치한 M 개의 사대(총을 쏘는 장소)에서만 사격이 가능하다. 편의상, 일직선을 x-축이라 가정하고, 사대의 위치 x1, x2, ..., xM은 x-좌표 값이라고 하자. 각 동물이 사는 위치는 (a1, b1), (a2, b2), ..., (aN, bN)과 같이 x,y-좌표 값으로 표시하자. 동물의 위치를 나타내는 모든 좌표 값은 양의 정수이다.

사냥꾼이 가지고 있는 총의 사정거리가 L이라고 하면, 사냥꾼은 한 사대에서 거리가 L 보다 작거나 같은 위치의 동물들을 잡을 수 있다고 한다. 단, 사대의 위치 xi와 동물의 위치 (aj, bj) 간의 거리는 |xi-aj| + bj로 계산한다.

예를 들어, 아래의 그림과 같은 사냥터를 생각해 보자. (사대는 작은 사각형으로, 동물의 위치는 작은 원으로 표시되어 있다.) 사정거리 L이 4라고 하면, 점선으로 표시된 영역은 왼쪽에서 세 번째 사대에서 사냥이 가능한 영역이다. 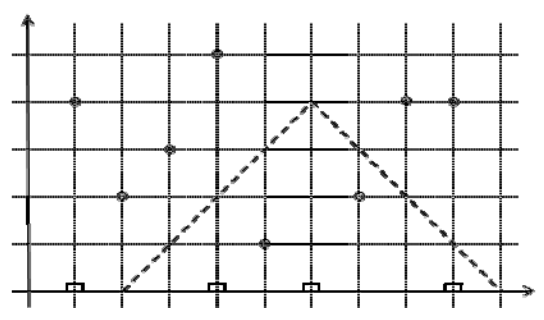사대의 위치와 동물들의 위치가 주어졌을 때, 잡을 수 있는 동물의 수를 출력하는 프로그램을 작성하시오.

입력
입력의 첫 줄에는 사대의 수 M (1 ≤ M ≤ 100,000), 동물의 수 N (1 ≤ N ≤ 100,000), 사정거리 L (1 ≤ L ≤ 1,000,000,000)이 빈칸을 사이에 두고 주어진다. 두 번째 줄에는 사대의 위치를 나타내는 M개의 x-좌표 값이 빈칸을 사이에 두고 양의 정수로 주어진다. 이후 N개의 각 줄에는 각 동물의 사는 위치를 나타내는 좌표 값이 x-좌표 값, y-좌표 값의 순서로 빈칸을 사이에 두고 양의 정수로 주어진다. 사대의 위치가 겹치는 경우는 없으며, 동물들의 위치가 겹치는 경우도 없다. 모든 좌표 값은 1,000,000,000보다 작거나 같은 양의 정수이다.

출력
출력은 단 한 줄이며, 잡을 수 있는 동물의 수를 음수가 아닌 정수로 출력한다.

풀이

이 분들의 글이 큰 도움이 됐다. 파이썬으로 문제를 푸시진 않으셨지만, 문제에 접근하는 법을 기술하신 부분이 잘 와닿았다.
https://zoosso.tistory.com/152
https://data-make.tistory.com/593
https://blog.naver.com/bestmaker0290/220820005454

비상식적인 속도의 공부를 소화해내고 있는 지금 난 많은 문제들을 그러했듯 이 문제도 풀이먼저 보고 어떻게 했는지 분석해보았다. 전형적인 이분탐색 풀이이나 문제를 어떻게 접근하는 가가 처음에 난해하였다.
(이렇게 현실감이 더해진 문제에 대한 해결을 수리적으로 접근, 코드화하는 것이 보다 더 어려운데 아마 갈 수록 더 그렇게 되겠지? 이런 건 어느정도 감각도 필요로 하는 거 같다... 하하.)

(사대 거리를 고정하고 가능한 동물 수를 구하려고 하면 시간 복잡도가 높아진다. - (n^2)
따라서 동물을 고정하고, 잡을 수 있는 사대가 존재하는 지 확인하는 하는 것이 쉽다. - (nlogn))

즉, N 마리의 동물이 M 개의 사대 중 자신을 잡을 수 있는 사대 한 개만 찾으면 된다.
단, 자신을 잡을 수 있는 사대를 찾을 때 TLE(Time Limit Exceeded)를 해결하기 위해 이분 탐색을 활용해야 한다.

아래의 코드는 점수 측정 시 만점의 정답이다.
for문을 돌리는 방식을 봤을 때 "동물의 입장에서 자신을 저격할 수 있는 사냥꾼의 위치를 탐색한다"는 말이 매우 명쾌한 정리 같다!

import sys
input = sys.stdin.readline
M, N, L = map(int, input().split())
shots = list(map(int, input().split()))
animals = []
for i in range(N):
    a, b = map(int, input().split())
    animals.append((a, b))

cnt = 0
shots.sort() # 사대의 위치는 반드시 오름차순 정렬해준다...

for a, b in animals:
    start, end = 0, len(shots)-1
    mid = 0
    
    while start < end: 			# for문 회차마다 해당 동물 좌표를 기준으로 
        mid = (start+end)//2    # 전체 사대 위치의 범위를 이분탐색하여 
        if shots[mid] < a: 		# 해당 동물로부터 가장 가까운 사대 인덱스 배출
            start = mid+1
        elif shots[mid] > a:
            end = mid-1
        else:
            start = mid
            break
	
    # 사대와 동물 간의 거리는? x좌표의 차이와 동물의 y좌표를 더한 값.
    if abs(shots[start]-a)+b <= L:
        cnt += 1
    elif start+1 < len(shots) and abs(shots[start+1]-a)+b <= L:
        cnt += 1
    elif start > 0 and abs(shots[start-1]-a)+b <= L:
        cnt += 1

print(cnt)

abs(a-x)+b => L에 해당하는 좌표의 동물이 각 사대에서 잡을 수 있는 동물!
그런데 무조건 L > b 인 경우만 해당된다.. 그렇지 않겠나, 수직에서도 총이 안 닿는다는데...

동물의 위치가 주어졌을 때, 동물에서 L 거리에 있는 사수 좌표(x축 위)의 범위는 거리를 구하는 식인 |x-a|+b 식을 를 이용해 쉽게 구할 수 있다.

우리가 찾고자 하는 범위의 최대거리인 L을 이용하면 x <= a ± (L-b) 이다. 이를 절댓값을 풀어 쓰면 a+b-L ≤ x ≤ a-b+L이 된다.

이 범위를 만족하는 사수 좌표 m을 찾기 위해, m 값들을 정렬하고 lower bound 알고리즘으로 m의 값들에서 a+b-L보다 크거나 같은 첫 좌표를 찾는다. 이 값이 a-b+L보다 작으면 범위 안에 사수가 하나 이상 있다는 뜻.

for문의 대상이 되는 동물의 위치를 하나씩 탐색하며,
a+(b-L) <= x <= a-(b-L)에 해당하는 위치에 사대가 있다면 해당 동물은 사냥 가능한 것으로 판단한 뒤 카운트.
아래의 부분은 각각 사냥꾼의 위치, 사냥꾼의 왼쪽 위치, 사냥꾼의 오른쪽 위치와 동물 사이의 거리가 L이하이면 카운트해주고 있는 코드들이다.

    if abs(shots[start]-a)+b <= L:
        cnt += 1
    elif start+1 < len(shots) and abs(shots[start+1]-a)+b <= L:
        cnt += 1
    elif start > 0 and abs(shots[start-1]-a)+b <= L:
        cnt += 1