외판원 순회 - 10971번
문제
외판원 순회 문제는 영어로 Traveling Salesman problem (TSP) 라고 불리는 문제로 computer science 분야에서 가장 중요하게 취급되는 문제 중 하나이다. 여러 가지 변종 문제가 있으나, 여기서는 가장 일반적인 형태의 문제를 살펴보자.
1번부터 N번까지 번호가 매겨져 있는 도시들이 있고, 도시들 사이에는 길이 있다. (길이 없을 수도 있다) 이제 한 외판원이 어느 한 도시에서 출발해 N개의 도시를 모두 거쳐 다시 원래의 도시로 돌아오는 순회 여행 경로를 계획하려고 한다. 단, 한 번 갔던 도시로는 다시 갈 수 없다. (맨 마지막에 여행을 출발했던 도시로 돌아오는 것은 예외) 이런 여행 경로는 여러 가지가 있을 수 있는데, 가장 적은 비용을 들이는 여행 계획을 세우고자 한다.
각 도시간에 이동하는데 드는 비용은 행렬 W[i][j]형태로 주어진다. W[i][j]는 도시 i에서 도시 j로 가기 위한 비용을 나타낸다. 비용은 대칭적이지 않다. 즉, W[i][j] 는 W[j][i]와 다를 수 있다. 모든 도시간의 비용은 양의 정수이다. W[i][i]는 항상 0이다. 경우에 따라서 도시 i에서 도시 j로 갈 수 없는 경우도 있으며 이럴 경우 W[i][j]=0이라고 하자.
N과 비용 행렬이 주어졌을 때, 가장 적은 비용을 들이는 외판원의 순회 여행 경로를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 도시의 수 N이 주어진다. (2 ≤ N ≤ 10) 다음 N개의 줄에는 비용 행렬이 주어진다. 각 행렬의 성분은 1,000,000 이하의 양의 정수이며, 갈 수 없는 경우는 0이 주어진다. W[i][j]는 도시 i에서 j로 가기 위한 비용을 나타낸다.
항상 순회할 수 있는 경우만 입력으로 주어진다.
출력
첫째 줄에 외판원의 순회에 필요한 최소 비용을 출력한다.
예제 입력
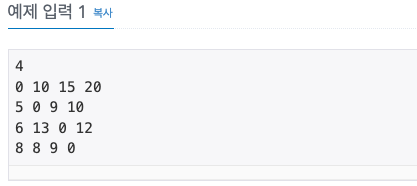
풀이
예제 입력의 모양을 보면 행렬의 구조를 띄고 있음을 볼 수 있다.
이 행렬을 이해하는 것이 첫 걸음이다.
입력되는 값이 뭔지 이해하면 어떻게 문제를 풀어야 하는지도 조금 더 잘 보인다.
입력은 우리가 흔히 떠올리는 지도의 형태처럼
가
아 니 라,
 의 데이터이다.
의 데이터이다.
만약 도시-도시-도시를 원한다면?
그것은  혹은
혹은
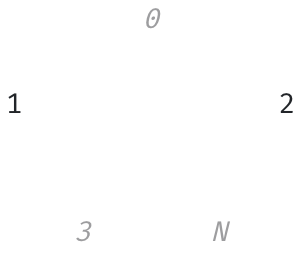 의 구조일 것이다.
의 구조일 것이다.
이는 즉 도시-도시-도시의 데이터는 어떤 모양인 것이 의미가 없단 뜻이기도 하다.
무언가를 이해하는 데에 시각적인 요소가 중요한 타입인지, 나같은 경우는 위와 같은 방식으로 이해하게 되었다. 도시들을 나타내는 지도가 일직선이고 도시와 도시를 오가는 비용의 표가 행렬의 구조이니 헷갈릴만 하였다.
어쨌든 바로 이 도시-도시-도시를 가지고 있는 데이터 역시 우리가 문제를 풀기 위해 필요하다.
우리는 시작과 동시에 바로 위의 이 도시-도시-도시 리스트 또한 만들 것이다.
처음 외판원 순회 문제에 대한 접근이 어려운 것은 이 개념을 이해하기 어려워서 였다. 위 개념을 이해하니 한결 쉬워졌다.
순열 - itertools
"도시->도시->..출발도시에돌아옴"의 모든 조합, 그런데 그 순서가 중요한 조합. 고로 문제 풀이에 순열의 개념이 쓰인다.
우선 순열로 푸는 방법을 연습했다.
아래는 일전에 위에서 언급했던 도시-도시-도시....-도시의 데이터다.
W = list(list(map(int, input().split())) for _ in range(N))다음의 코드는 도시->도시->...도시의 모든 순열조합에 대한 데이터이다.
permuts = list(permutations(range(N)))함수를 적어내려갈 때에 가장 먼저, 큰 그림으로써, 순열조합을 for문 돌린다는 걸 기억한다면 그 안에서 순열조합으로 얻어내야 할 정보와 그에 따른 수행문, for문을 탈출할 조건문 이 2가지를 미리 머릿속에 가지고 있어야 한다는 점도 기억할 수 있다.
조합들의 집합을 permuts, 조합 하나를 perm이라고 했을 때
예를 들어 perm = (0,1,2,3) 이다.
가장 먼저 우린 W[0][1], W[0][2], W[0][3], W[0][4]의 합에 대한 정보를 알고 싶다(큰 그림 안 작은 그림으로써의 for문이다.).
고로 아래와 같은 코드가 정답 안에 포함될 것을 이해할 수 있다.
for i in range(N-1):
sum += W[perm[i]][perm[i+1]]그리고 만약 W[perm[i]][perm[i+1]] 가 0 이면 "도시 i"에서 "도시 i+1"으로 못 간단 말이니, for문을 빠져나올 것이다. 고로 아래와 같은 코드를 떠올릴 수 있다.
for i in range(N-1):
.
.
... if W[perm[i]][perm[i+1]]==0:
....
break그런데 만약 우리가 맨 마지막 도시에서 처음의 도시로 돌아오는 길에 없는 경우라면, 데이터와 시간을 낭비할 필요 없이 for문의 시작에 앞서 이러한 경우부터 거르고 들어가도 될 것이다.
if W[perm[-1]][perm[0]]==0:
continue
.
.이런 식으로 풀이를 위에서부터 아래로 적어내려가는 게 아니라 수행의 순서와 논리대로 생각해보며 함수를 접근했다.
다음의 코드는 정답이다.
참고로 순열로 이 문제를 풀면 시간초과가 난다. 그래서 승훈이가 알려준 꿀팁으로 모든 코드를 def 안에 넣었더니 시간과 데이터가 축약되었다. 이는 요령이라 쓸모가 있지만 궁극적으로 이 꼼수가 대수는 아닐 것이다...
def dfs():
import sys
from itertools import permutations
input = sys.stdin.readline
N = int(input())
W = list(list(map(int, input().split())) for _ in range(N))
cities = list(permutations(range(N)))
currMin = 1e9
for city in cities:
sum = 0
flag = True
if W[city[-1]][city[0]] == 0:
continue
for i in range(N-1):
if W[city[i]][city[i+1]] == 0:
flag = False
break
sum += W[city[i]][city[i+1]]
if flag:
sum += W[city[-1]][city[0]]
currMin = min(sum, currMin)
print(currMin)
dfs()순열 - 재귀
위 풀이 중 itertools로 조합을 만든 걸 고대로 재귀함수로 구현한 것만 빼곤 동일한 풀이이다.
아래의 풀이는 정답이다.
import sys
input = sys.stdin.readline
N = int(input())
W = list(list(map(int, input().split())) for _ in range(N))
arr = [0]*N
p = []
permuts = []
def permu(n):
global p
if n==N:
permuts.append(p)
return
for i in range(N):
if arr[i]==0:
arr[i] = 1
p.append(i)
permu(n+1)
arr[i] = 0
p = p[:-1]
permu(0)
currMin = 1e9
for perm in permuts:
sum = 0
flag = True
if W[perm[-1]][perm[0]] == 0:
continue
for i in range(N-1):
if W[perm[i]][perm[i+1]] == 0:
flag = False
break
sum += W[perm[i]][perm[i+1]]
if flag:
sum += W[perm[-1]][perm[0]]
currMin = min(sum, currMin)
print(currMin)이 풀이는 사실 의미 없다. 그냥 순열 만드는 연습을 한 거다.
백트래킹(dfs)
이 문제는 본디 백트래킹으로 접근하는 것이 정수이다. 백트래킹 역시 재귀 함수를 사용하는 풀이 기법이며 마치 저번의 카드놓기 문제와 같다. 그때 날 잡고 그렇게 파길 잘했다...
백트래킹은 기본적으로 이 visited 기법을 쓴다.
visited = [0]*N
if 보통depth==N이고아니면다른인자==어쩌고저쩌고탈출조건:
...
return
for i in range(N):
visited[i] = 1
dfs(depth+1, 어쩌고, 인자+1, 인자//2 ...)
visited[i] = 0이번 문제 풀면서 재귀 함수 사용 시 인자가 많으면 어렵다고 생각했는데 아니었다. 함수 인자로 변수를 선언하는 것이 오히려 속 편하다는 것을 알았다.
다음의 코드는 정답이다.
import sys
input = sys.stdin.readline
N = int(input())
W = list(list(map(int, input().split())) for _ in range(N))
currMin = 1e9
visited = [0]*N
def dfs(depth, current, sum):
global currMin
if depth==N-1 and W[current][0]!=0:
sum+=W[current][0]
if sum<currMin:
currMin = sum
return
for i in range(N):
if visited[i]==0 and W[current][i]!=0:
visited[i] = 1
dfs(depth+1, i, sum+W[current][i])
visited[i] = 0
visited[0] = 1
dfs(0, 0, 0)
print(currMin)하하~ 그렇게 오랜 시간 내 맘을 불편하게 한 외판원 순회를 해냈다. 짧은 기간 안에 이렇게 늘었단 사실이 너무 좋다~
도움 받기 전 for문의 i를 인자로 설정하고 싶은데 어케 하는지 몰랐다가 팀원 현지님의 도움으로 인자 current의 활용을 깨우쳤다. start라는 인자를 쓰고 싶었는데 for문의 맨 처음이 0인 점을 이용해 그냥 if visited[i]==0 and W[current][i]!=0:라고 표기했더니 됐다.