콜라츠 추측
문제 설명
1937년 Collatz란 사람에 의해 제기된 이 추측은, 주어진 수가 1이 될 때까지 다음 작업을 반복하면, 모든 수를 1로 만들 수 있다는 추측입니다. 작업은 다음과 같습니다.
1-1. 입력된 수가 짝수라면 2로 나눕니다.
1-2. 입력된 수가 홀수라면 3을 곱하고 1을 더합니다.
2. 결과로 나온 수에 같은 작업을 1이 될 때까지 반복합니다.
예를 들어, 주어진 수가 6이라면 6 → 3 → 10 → 5 → 16 → 8 → 4 → 2 → 1 이 되어 총 8번 만에 1이 됩니다. 위 작업을 몇 번이나 반복해야 하는지 반환하는 함수, solution을 완성해 주세요. 단, 주어진 수가 1인 경우에는 0을, 작업을 500번 반복할 때까지 1이 되지 않는다면 –1을 반환해 주세요.
제한 사항
입력된 수, num은 1 이상 8,000,000 미만인 정수입니다.
입출력 예
n result
6 8
16 4
626331 -1
풀이 과정
function solution(n) {
let i=0;
do {
n%2 ? n=n*3+1 : n=n/2;
i++;
if (n==1) {
break;
}
if(i>=500) {
i = -1;
break;
}
} while(n!==1);
return i;
}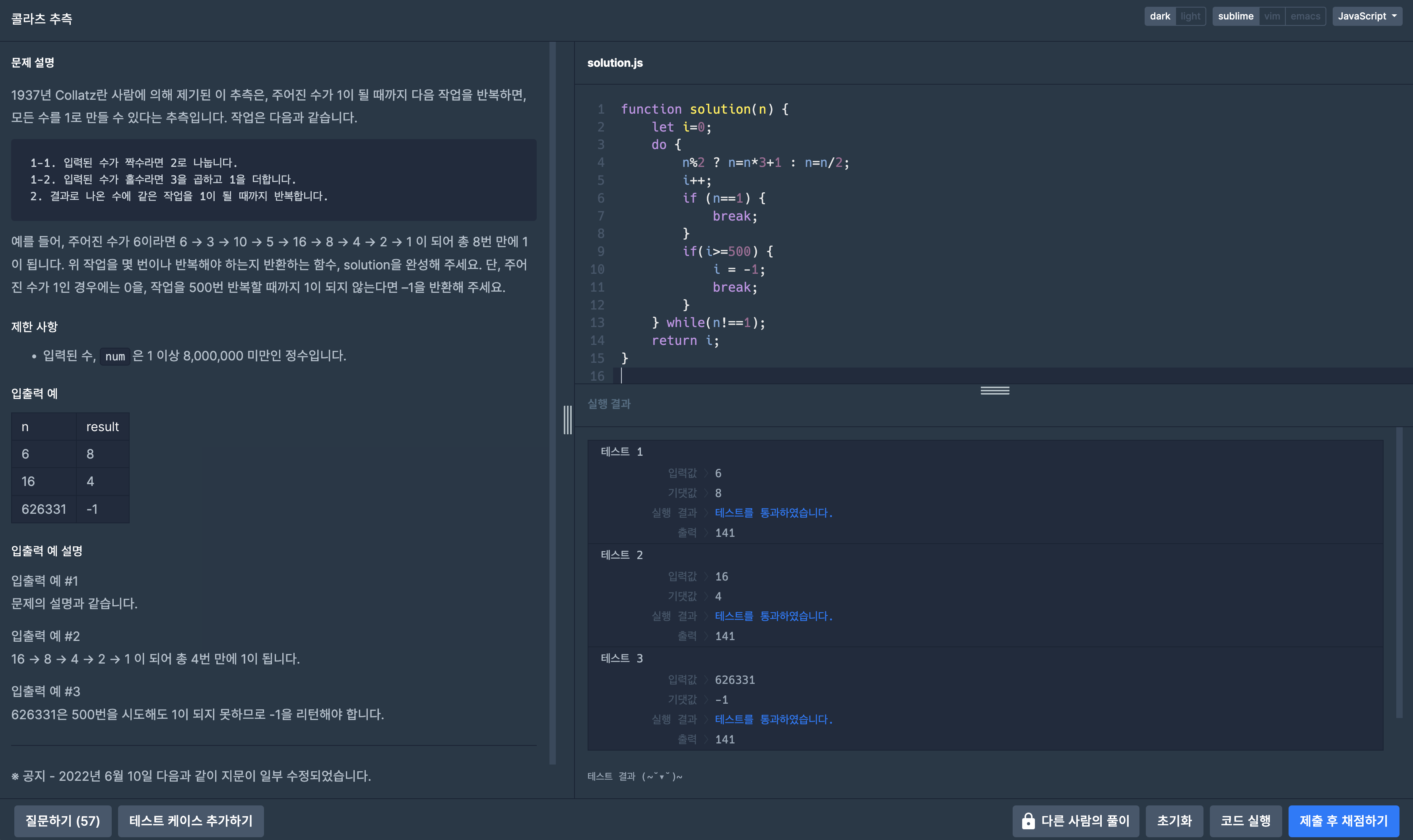
위 답안을 다 쓴 뒤 if(i>=500)이 확실히 정답인지 더블체크하였다.
맞는 것 같아서 제출했는데 틀렸다. 알고 보니 문제에 기재되어 있는 n이 1인 경우를 작성하지 않았다.
function solution(n) {
if (n===1) {
return 0;
} else {
let i=0;
while (n!==1){
i++;
n = n%2 ? n*3+1 : n/2;
if (n==1) {
return i;
break;
}
if(i>=500) {
return -1;
break;
}
}
}
}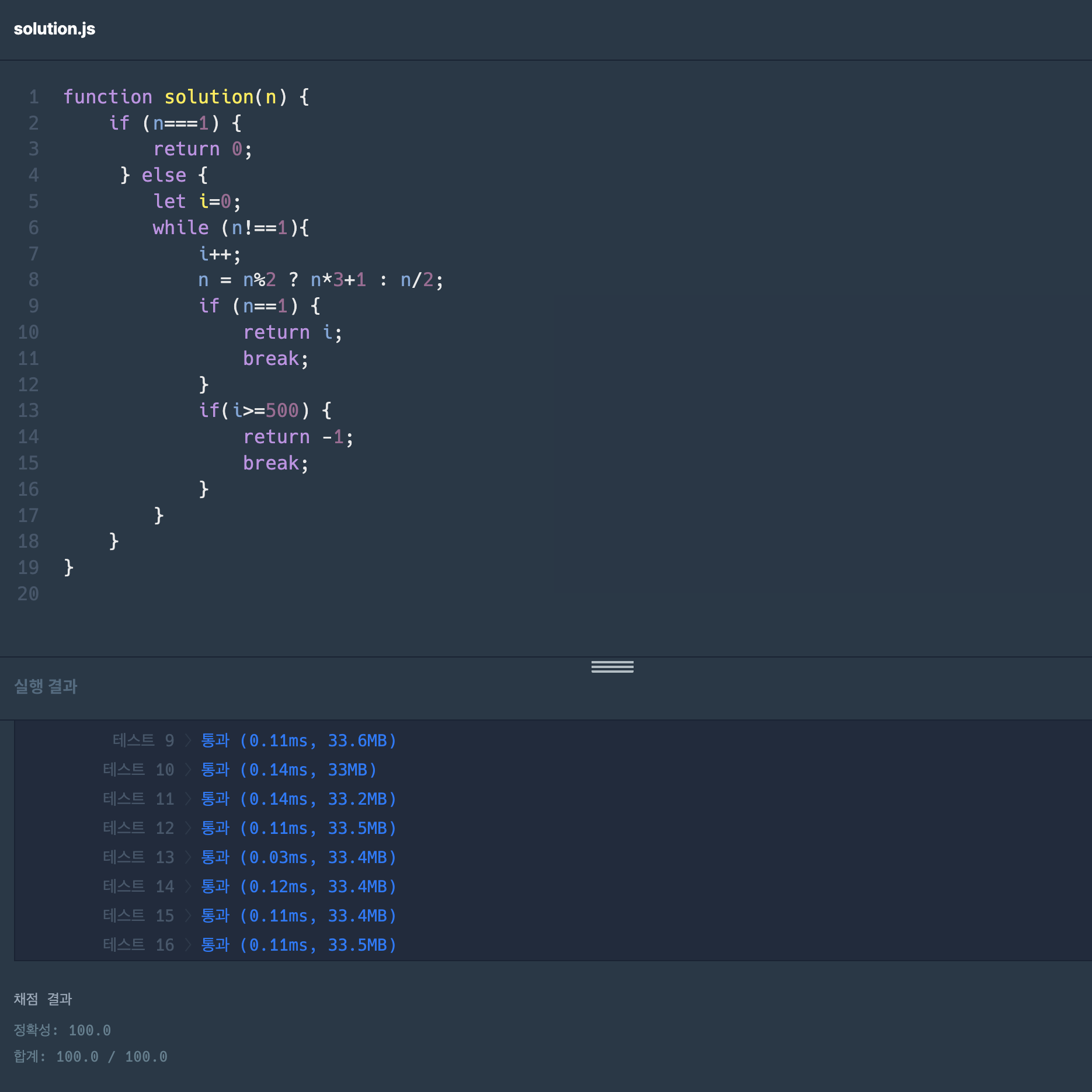
통과했다.
1
재귀를 이용한 답안이 보기에 간결했다.
function solution(num, i=0) {
return num==1 ? (i>=500 ? -1 : i) : solution(num%2==0 ? num/2 : num*3+1, ++i);
}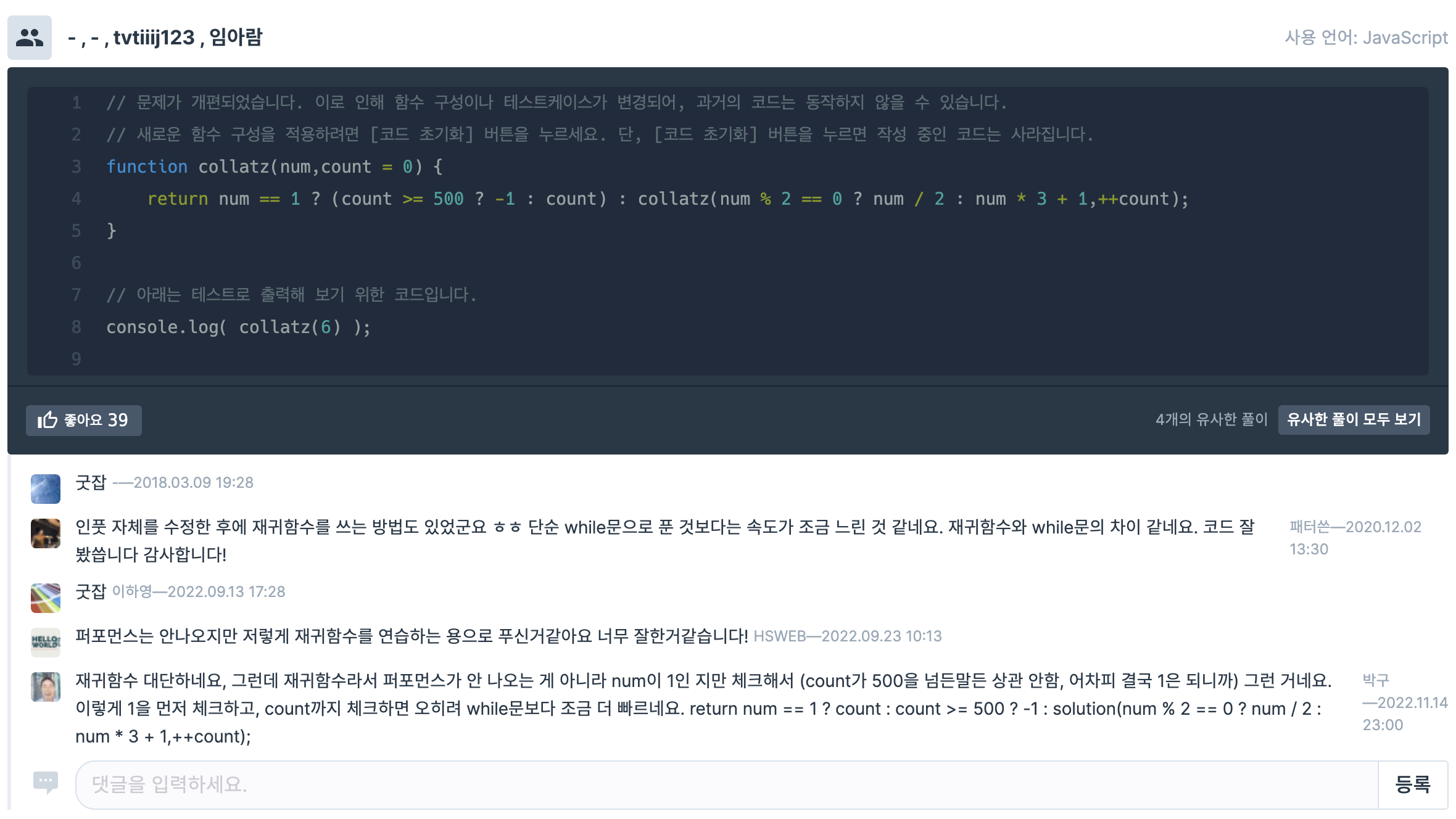
재귀는 기본적으로 이런 꼴을 한다.
function solution(num, i=0) {
return _ ? _ : solution (_ ? _ : _)
}
그런데 이 문제에선 n===1일 경우 return 0; 때문에 한 번 더 조건문이 붙는다.
function solution(num, i=0) {
return _ ? ( _ ? _ : _ ) : solution( _ ? _ : _ );
}
다시 한 번 보고 내 답을 수정해보았다.
function solution(num, i=0) {
return num===1 ? (i>=500 ? -1 : i) : solution(num%2 ? num*3+1 : num/2, ++i);
}