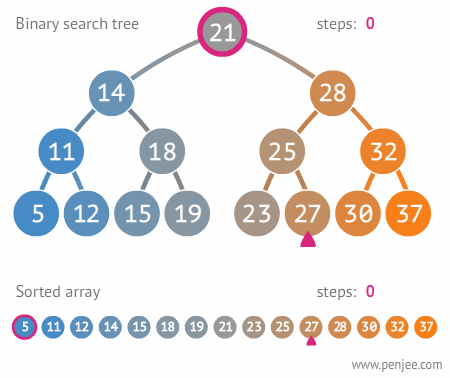
정렬된 배열 to 최적이진탐색트리
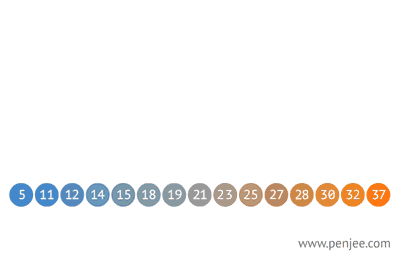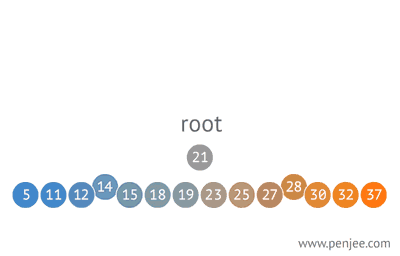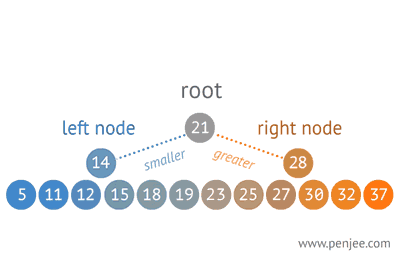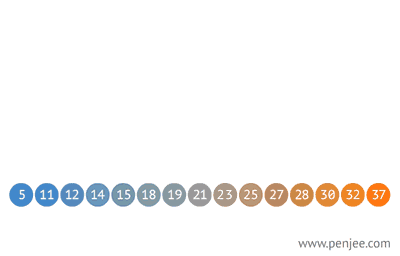
이진탐색에 대해
탐색기법 중 하나인 이진탐색(binary search)는 정렬된 배열에 대한 탐색기법으로, 정렬된 배열에 대해선 O(logN)의 성능을 보여준다.
하지만 해당 이진탐색은 선행하여 수행된 정렬 알고리즘의 성능을 포함하고 있는 값이다. 만일 삽입/삭제( O(N) ) 등의 연산수행으로 이진탐색 대상 배열의 정렬상태가 깨어진다면 최악의경우 시간복잡도는 O(N)까지 떨어질 수 있으며, 이 경우 다시 이진탐색을 사용하기 위해 정렬을 수행한다.
이러한 이유로 만일 삽입/삭제가 빈번한 시스템에서 이진탐색을 사용할 경우 그 효율이 크게 떨어진다.
따라서 삽입 / 삭제 / 탐색 모두 빈번하게 사용하는 시스템의 경우 이진탐색트리를 자료구조로 사용해야 한다.
이진탐색트리 Binary Search Tree : BST
이진탐색과 기본 원리는 동일하나, 배열이 아닌 트리를 사용한 자료구조이다.
이진탐색트리의 성립 조건 : 왼쪽서브트리의 모든 탐색값은 부모노드보다 작아야하며, 오른쪽 서브트리의 모든 탐색값은 부모노드보다 커야한다. 모든 자식노드의 서브트리 또한 이진탐색트리이다.
이진탐색트리는 삽입, 삭제, 탐색 연산에서 모두 O(logN)의 성능을 보장한다.
-
삽입 : 삽입할 탐색값의 탐색 실패 위치에 삽입하면 된다.
-
삭제
- 1. Leaf노드의 삭제 : 해당 노드만 삭제한다.
- 2. L or R 자식노드가 1개 : 제거한 뒤 자식노드를 해당 자리로 승계한다.
- 3. L and R 자식노드가 2개 :
서브트리의 모든 값 중, 제거할 노드에 가장 가까운 값을 후계로 승계한다.
해당 후계값은 왼쪽 서브트리의 가장 큰 값이거나 오른쪽 서브트리의 가장 작은 값일 것이다. 만일 값이 동일할 시 둘 중 하나를 임의로 정한다.
-
탐색 : 이진탐색과 동일
이진탐색트리의 탐색
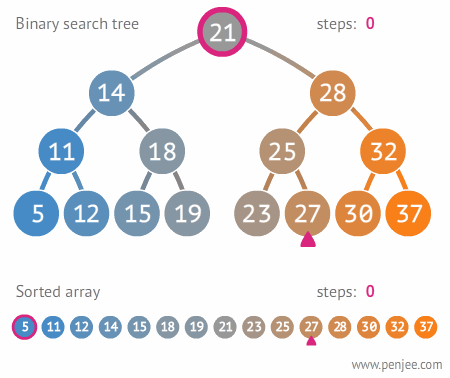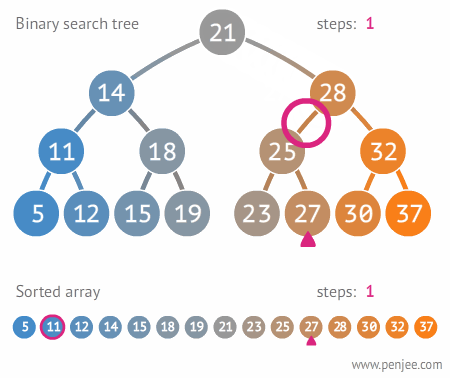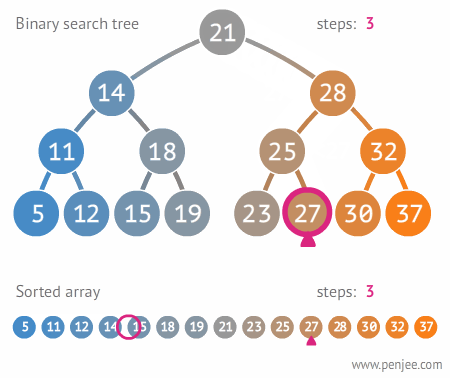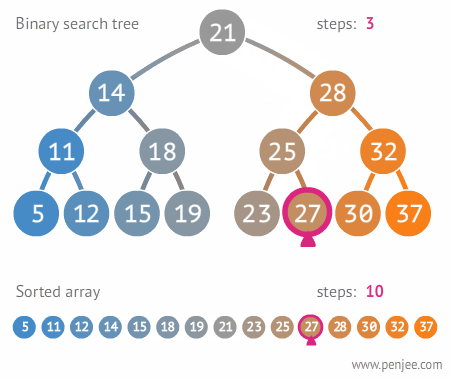 ]
]
이진탐색 트리의 삽입(구성)

하지만 이진탐색트리도 단점이 존재한다. 트리라는 구조의 특성으로 인해, 삽입 삭제로 인해 트리의 균형이 무너져 노드 수 대비 상대적으로 높이가 커질수록 모든 연산의 효율이 성능이 떨어지게 된다, 즉 연산의 시간과 트리의 높이는 비례한다.
균형이 완전히 깨어진 경사트리가 탐색효율이 가장 낮으며 이경우를 최악의 경우로 상정하여 [키 탐색, 값 탐색, 최대/최소 탐색, 삽입, 삭제] 모든 연산이 O(N)의 성능을 보인다.
반면 균형을 완벽히 유지하는 포화이진트리의 경우 높이가 낮기에 가장 좋은 성능을 보이는 최선의 경우이며, 값 탐색의 O(N)을 제외하고 모든 연산이 O(logN)의 성능을 보장한다.
이러한 이진탐색트리의 불균형으로 인한 높이차로 인해 발생하는 성능 불균형 단점을
삽입 이후 REBALANCING 함수(재균형)를 수행함으로써 트리를 균형화하여 해결할 수 있다.균형이진탐색트리 (AVL)
균형이진탐색트리의 단점부터 언급하고 넘어가겠다.
AVL트리는 탐색성능의 O(logN)을 완벽히 보장하기 위한 자료구조이다.
AVL의 삽입 이후 사용하는 REBALANCING으로 진행되는 구조화 그 자체가 오버헤드를 발생시킨다.
따라서 삽입이 빈번하지 않은 탐색을 위한 시스템에 더욱 적합하다.균형 인수 (Balance Factor)
균형 인수는 삽입 이후 발생할 수 있는 불균형을 판단하기 위한 요소이다.
균형인수가 +-1 의 범위를 초과할 경우 불균형 하다고 판단하고 Rebalancing을 진행한다.
균형인수 값 구하기
1. 트리의 Bottom-Up으로 각 노드 서브트리의 높이를 구한다.
-> 높이는 해당 노드의 자식노드 둘의 높이를 인자로, Max(L,R) +1 결과값을 사용한다
2. 왼쪽 자식트리 높이 - 오른쪽 자식트리 높이, 로 균형인수를 구한다.
- Leaf Node는 0의 균형인수를 갖는 구조이다.
- 공집합 노드(서브트리)의 높이는 -1로 간주한다.
3. 균형인수의 해석
- 균형인수가 양수라면 왼쪽으로 편향된 불균형
- 균형인수가 음수라면 오른쪽으로 편향된 불균형
4. 불균형 세부 타입
불균형의 세부 타입에는 LL, LR, RR, RL로 총 네가지 타입이 있으며 각각 다른 리밸런싱을 적용,
1. LL타입 : 균형인수가 2,1 순서로 왼쪽으로 쭉 내려가서 LEFT LEFT로 이어지는 불균형
-> 시계방향 회전
2. LR타입 : 균형인수가 2, -1 순서로 왼쪽 이후 오른쪽으로 꺾어져 LEFT RIGHT로 이어지는
불균형
-> RR회전,LL회전 순서로 적용하여 ( 반시계 회전, 시계 회전) 수행
3. RR 타입 : 균형인수가 -2, -1 순서로 오른쪽 오른쪽으로 연속 편향된 경우이다.
-> 반시계방향 회전
4. RL 타입 : 균형인수가 -2 1 순서로 오른쪽 이후 왼쪽으로 꺾인 편향의 경우
-> LL회전 RR회전 수행, (반시계 회전, 시계 회전)
