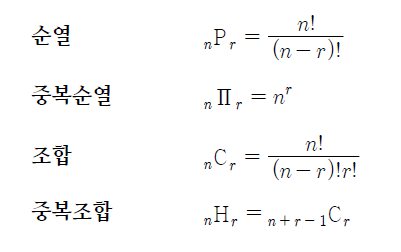순열이란?

주어진 목록 중 일부를 골라 중복없이 나열하는 것
순서를 고려한 것으로, 나열한 값이 같아도 순서(위치)가 다르다면 다른 경우의 수

n개 중 r개를 선택한 경우의 수
nPr = n! / (n - r)!

반복문으로 구현 가능하나 비효율적이다.

주어진 목록(배열)의 요소 n개 중에 r개를 사용해 조합하는 순열은
배열을 r번 반복하여 구해야 하기 때문에 r겹 반복문이 필요하다.
이는 동적이지 못하며 매우 복잡하고 비효율적이다.

function rockPaperScissors () {
  let chance = ['rock', 'paper', 'scissors']
  let result = []

  for (let i = 0; i < 3; i++) {
    for (let j = 0; j < 3; j++) {
      for (let k = 0; k < 3; k++) {
        if (i === j || j === k || k === i) continue; 
        result.push([chance[i], chance[j], chance[k]])
      } 
    }
  }
  return result
}; // 가위바위보 3판의 경우의 수

몇 개를 뽑는지 미리 알아야 반복문 가능

조합이란?

순서가 없는 경우의 수로, 앞서 택한 값은 또 선택할 수 없다.

isIsogram

function isIsogram(str) {

  str = str.toLowerCase();
  
  for (i = 0; i < str.length; i++) {
    for (j = i + 1; j < str.length; j++) {
      if (str[i] === str[j]) return false;
    }
  }
  return true;
}

---

템플릿

여러 방법으로 풀어보다가 내가 가장 잘 이해할 수 있는 접근법을
이쁘게 리팩토링해서 템플릿으로 만들어 봤다.

인자1: 선택할 수 있는 요소를 담은 배열
인자2: 요소를 선택할 수 있는 개수

중복 순열

재귀 함수를 이용해 반복문을 r겹 만들고 완성하면 종료하도록 하자.

  let cases = []; // 경우의 수 넣을 배열

  function rPermutation (arr, bucket, num) { 
    if (!num) { // r겹 반복문을 완성하면 리턴하라.
      cases.push(bucket) 
      return;
    }  
    arr.forEach(el => rPermutation (arr, [...bucket, el], num - 1)) 
  }
  rPermutation (인자1, [], 인자2) 
  return cases;
};

순열

중복 순열은 모든 경우를 구하면 되지만, 순열은 사용한 요소는 목록에서 제외해야 한다.

사용한 요소만 없애버리자!

  let cases = [];

  function permutation (arr, bucket, num) {
    if(!num) { 
      cases.push(bucket)
      return;
    }
    arr.forEach((el, idx) => {
      let copy = arr.slice() 
      copy.splice(idx, 1) // 선택한 el 제외 -> splice는 원본을 건드린다.
      permutation (copy, [...bucket, el], num - 1) 
    }) 
  }
  permutation (인자1, [], 인자2) 
  return cases;
}

조합

앞서 사용한 것은 모두 제외한다!

  let cases = [];
  let conbination = (arr, bucket, num) => {
    if (!num) {
      cases.push(bucket);
      return;
    }
    arr.forEach((el, idx) => conbination (arr.slice(idx + 1), [...bucket, el], num - 1))
  }
  conbination(인자1, [], 인자2)
  return cases;

최대 공약수

GCD; Greatest Common Divisor: 공약수 중에서 최대인 수

const gcd = (a, b) => a % b === 0 ? b : gcd(b, a % b);

최소 공배수

LCM; Least Common Multiple: 공배수 중에서 최소인 수

const lcm = (a, b) => a * b / gcd(a, b);