컴퓨터는 소수를 어떻게 표현할까?
컴퓨터에서 소수를 다루는 상황은 자주 발생한다.
하지만 10진수를 사용하는 사람과 달리 컴퓨터는 2진수를 사용한다.
컴퓨터는 소수를 어떻게 표현할까?
두 가지 표현 방식을 배울 것이다.
- Fixed Point
- Floating Point
포스트의 제목이 Floating Point 이기 때문에 물론 Floating Point 가 더 중요하다.
1. Fixed Point
첫 번째 방법은 Fixed Point 이다.
2진수로 숫자를 표현할 때, 정수 부분은 2^n으로 표현된다.
이 표현 방법은 소수 부분 또한 같은 방식을 취한다.
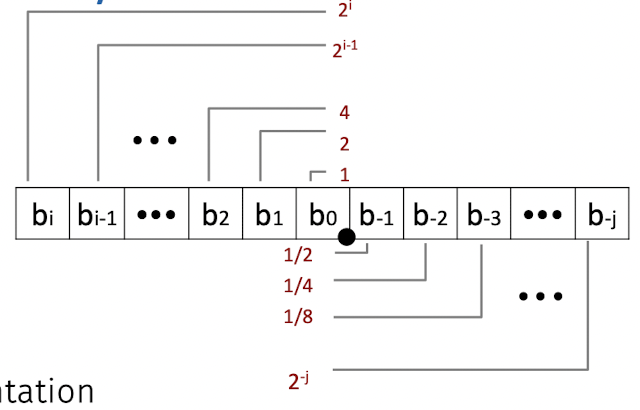
소수점 아래 숫자들은 각각 1/2^n을 표현한다.
EX) 101.11 = 5 + 3/4 같은 방식이다.
하지만 이러한 방식에는 한계가 존재한다.
Limitation of Fixed Point - 1
첫 번째 한계는 x/2^k의 수 이외에는 표현할 수 없다는 점이다.
예를 들면 분모가 3, 5 인 수들은 표현할 수 없다.
1/3을 이 방식으로 표현해 보자.
1/3 = 0.01010101010101...
1/5 = 0.0011001100110011...
이렇게 무한히 소수 부분이 길어지게 된다.
Limitation of Fixed Point - 2
두 번째 한계는 소수점이 고정되어 있어 w 비트에서 한정된 범위의 수만을 표현할 수 있다는 점이다.
w 비트를 사용하여 소수를 표현할 때, Fixed Point에서는 소수 부분에 할당해야 하는 비트가 고정되어 있고, 그 말은 즉 남는 비트만을 활용해 정수 부분을 표현해야 한다는 것인데, 이는 표현할 수 있는 수의 크기에 제한을 주게 된다.
2. Floating Point
오늘의 주인공이다.
Fixed Point의 한계를 극복하기 위해서 IEEE에서 개발한 소수 표현 방식이다.
Floating Point는부동소수점이라고 표현하기도 하는데, 여기서 '부동' 은 '움직이지 않는다'의 의미가 아니라, '떠다닌다' 라는 의미다.
현재 대부분의 컴퓨터가 이 방식을 따른다. 어떻게 소수를 표현하는지 알아보자.
표현 방식을 숫자로 보면 (-1)^S M 2^E 이다.

위 그림은 bit를 표현한 것이다. 맨 앞의 S는 위 숫자 표현 방식을 통해 알 수 있듯, 부호를 결정하는 역할을 한다. s = 0 이면 수는 양수가 되고, s = 1 이면 수는 음수이다.
다음 exp 영역은 숫자 표현 방식의 E를 의미한다.
frac 영역은 숫자 표현 방식의 M을 의미한다.
숫자 표현 방식의 M은 1.0이상 2.0 미만의 숫자를 나타낸다.
이후 M에 2^E을 곱해서 나온 수가 우리가 표현하고자 하는 수가 된다.
Floating Point - Normalized Values
우선 Normalized Value들의 표현 방법을 알아보자.
Normalized Value 들은 exp영역이 000...0 혹은 111...1 처럼 0 이나 1로 꽉 채워지지 않은 수들이다.
그 말은 즉 exp 영역이 전부 0 이거나 1이면 Denormalized Value 이라는 뜻이고, 이 내용 다음에 설명하도록 하겠다.
Normalized Value(v)를 구하는 방법은 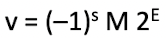 이다.
이다.
우선 E부터 알아보자. bit의 exp영역에 들어가 있는 bit, 그러니까 수를 Exp라고 하겠다.
exp영역에 들어 있는 bit들의 값(Exp) 을 바로 E에 대입하는 것이 아니다.
bias라고 하는 값을 Exp에서 빼주는 과정을 거쳐야 한다.
여기서 bias는 숫자를 표현하는 bit수에 따라 달라지게 된다.
설명의 기준은 float(32bit)로 하겠다.
bias는 2^(k-1) -1 인데, 여기서 k는 숫자를 표현 할 때 사용하는 exp영역의 bit수가 된다.
32bit float를 예로 했을 때, float에서는
- s 영역 1 bit
- exp 영역 8 bit
- frac 영역 23 bit
이다. 이 값은 정해져 있는 것이다.
그렇다면 32 bit로 표현되는 float에서의 bias의 값은 2^(8-1) -1 = 127이다.
따라서 구하고자 하는 값 v 를 나타내는 공식에서, 우리가 사용하게 되는 E의 값은, exp 영역에
들어 있는 수 - 127인 것이다.
그렇다면 M은 무엇일까?
frac 영역은 우리가 표현하고자 하는 수의 가장 큰, 왼쪽 Most Significant Bit를 제외한 수들이다.
EX) 15213 = 11101101101101 인데,
frac 영역은 여기서 가장 왼쪽 1을 제외한 값이다. 따라서 110110110101이 된다.
아까 M은 1이상 2미만이라는 것을 기억하는가?
M은 따라서 frac영역 앞에 1. 을 붙인 값이다.
이렇게 구한 모든 값들을 곱하면 우리가 표현하고자 하는 수가 되는 것이다.
우리가 표현하고자 하는 수를 구하는 공식과, 실제로 bit에 저장되는 값이 차이가 있다.
Floating Point로 값을 나타내는 법을 함께 해보자.
예시
706.625를 표현하고 싶다.
706.625를 처음 소개했던 Fixed Point 방식으로 표현하면,
1011000010.101이다. 여기서 우리는 소수점을 이동시킬 것이다.
제일 큰 비트와 두번째 비트 사이로 이동시킨다.
1.011000010101이 되는데, 여기서 제일 큰 비트에 있는 1은 제외하고, 소수점 오른쪽 부분의 수들이 우리의 frac영역에 들어가는 비트가 된다.
그렇다면 우리가 가진 1.011000010101이 표현하고자 하는 706.625가 되려면, 2의 몇 제곱을 곱해줘야 할까?
2^9를 곱해주면 된다. 따라서 우리의 exp영역의 수에서 bias = 127을 빼준 E값이 9가 되어야 한다는 것이므로 exp영역에는 136이라는 수가 있어야 한다.
따라서 실제 32bit 내에 들어가는 수는,

이다.
Floating Point - Denormalized Value
Denormalized Value는 exp영역의 값이 000...0 이거나, 111....1인 경우를 말한다.
Denormalized Value - exp = 000....0
exp가 전부 0인 경우를 알아보자.
이 경우 내에서도 두 가지 경우로 나뉠 수 있다.
frac 의 값이 000...0 이거나, 아닌 경우이다.
전자의 경우, 값은 zero value를 의미한다.
후자의 경우는, 0.0에 가까운 수를 나타낸다.
Denormalized Value - exp = 111....1
exp가 전부 1인 경우를 알아보자.
이 경우 또한 두 가지 경우로 나뉜다.
frac의 값이 000...0인 경우와 아닌 경우이다.
전자는 infinity, 무한대를 의미한다.
후자는 Not-a-Number(NaN)를 나타낸다. sqrt(-1) 등의 숫자가 아닌 값을 표현할 때 사용한다.
Limitation of Floating Point
Fixed Point와 마찬가지로, Floating Point 또한 소수들의 정확한 값을 나타낼 수 없다.
우리가 사용하는 Floating Point를 이용한 소수의 표현은 근사치라는 점을 알아 두자.
하지만 Fixed Point가 표현할 수 있는 수의 범위가 제한적이라는 한계점은 Floating Point가 극복할 수 있다.
