트리 (Tree)

노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조

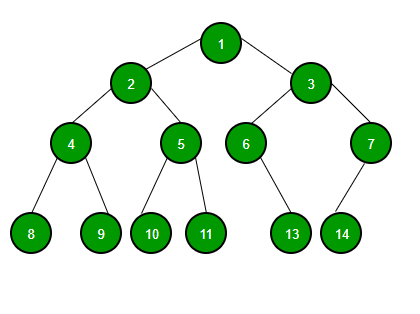
트리는 하나의 루트 노드를 갖는다.

루트 노드는 0개 이상의 자식 노드를 갖고 있다.

그 자식 노드 또한 0개 이상의 자식 노드를 갖고 있고, 이는 반복적으로 정의된다.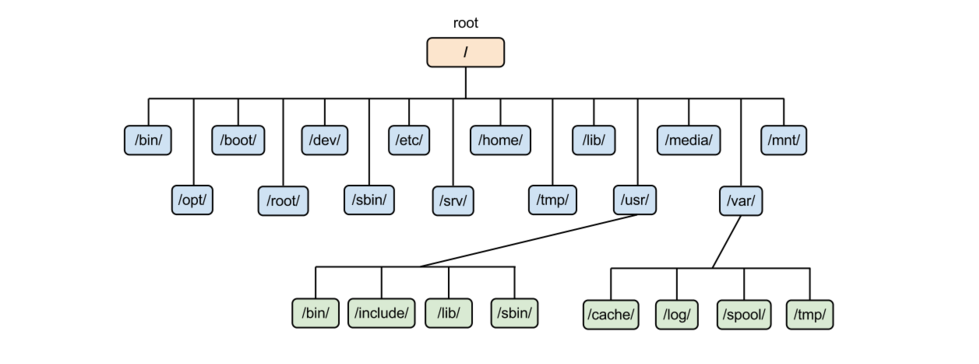

컴퓨터의 direcory구조가 트리 구조의 대표적인 예가 될 수 있다.

---

트리(Tree) 용어 정리

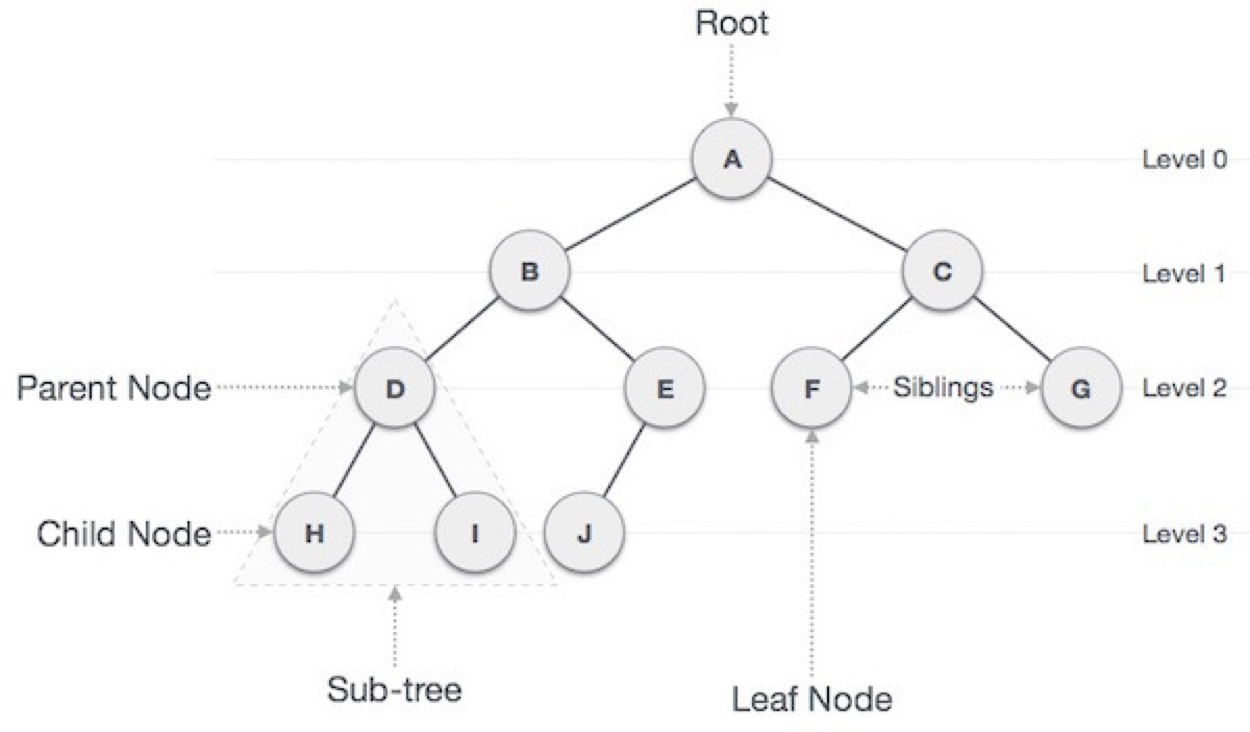
• 루트 노드(root node): 부모가 없는 노드, 트리는 하나의 루트 노드만을 가진다.
  > A

• 내부(internal)노드 : 단말 노드가 아닌 노드
  > A B C D E

• 단말 노드(leaf node): 자식이 없는 노드, ‘말단 노드’ 또는 ‘잎 노드’라고도 부른다.
  > F G H I J

• 간선(edge): 노드를 연결하는 선 Link, branch 라고도 부른다.

• 형제(sibling) : 같은 부모를 가지는 노드
  > H I

• 노드의 크기(size): 자신을 포함한 모든 자손 노드의 개수

• 노드의 깊이(depth): 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수

• 노드의 레벨(level): 트리의 특정 깊이를 가지는 노드의 집합
  > root 노드부터 level0

• 노드의 차수(degree): 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수

• 트리의 차수(degree of tree): 트리의 최대 차수

• 트리의 높이(height): 루트 노드에서 가장 깊숙히 있는 노드의 깊이

• Order : 부모 노드가 가질 수 있는 최대 자식의 수
  > Order 3 : 부모 노드는 최대 3명의 자식을 가질 수 있다.

• Breadth : 리프 노드의 수
  >Breadth : 5

---

트리(Tree)의 특징

• 트리에는 사이클이 존재할 수 없다.

• 모든 노드는 자료형으로 표현이 가능하다.

• 루트에서 한 노드로 가는 경로는 유일한 경로 뿐이다.

• 노드의 개수가 N개면, 간선은 N-1개를 가진다.

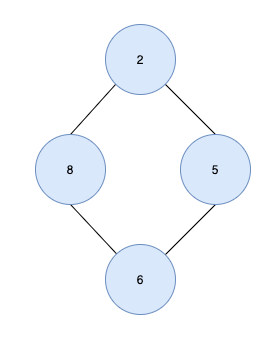
노드 6에는 2명의 부모 노드(8,5)가 있고 사이클(2-8-6-5)이 형성되므로 트리가 아니다.

그래프와 트리의 차이는 사이클의 유무이다

---

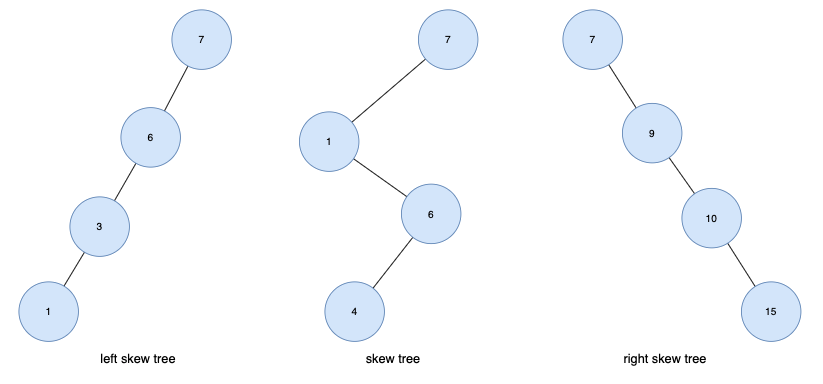
트리(Tree) 종류

• 편향 트리 (skew tree)
  모든 노드들이 자식을 1개만 가진 트리
  왼쪽 방향으로 자식을 하나씩만 가질 때 left skew tree,
  오른쪽 방향으로 하나씩만 가질 때 right skew tree라고 한다.

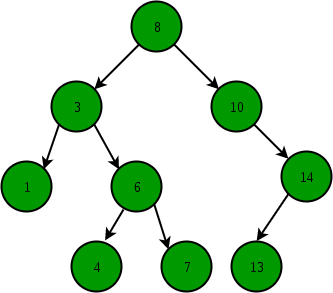
• 이진 탐색 트리 (Binary Search Tree, BST)
  순서화된 이진 트리
  노드의 왼쪽 자식 < 부모의 값
노드의 오른쪽 자식 > 부모의 값

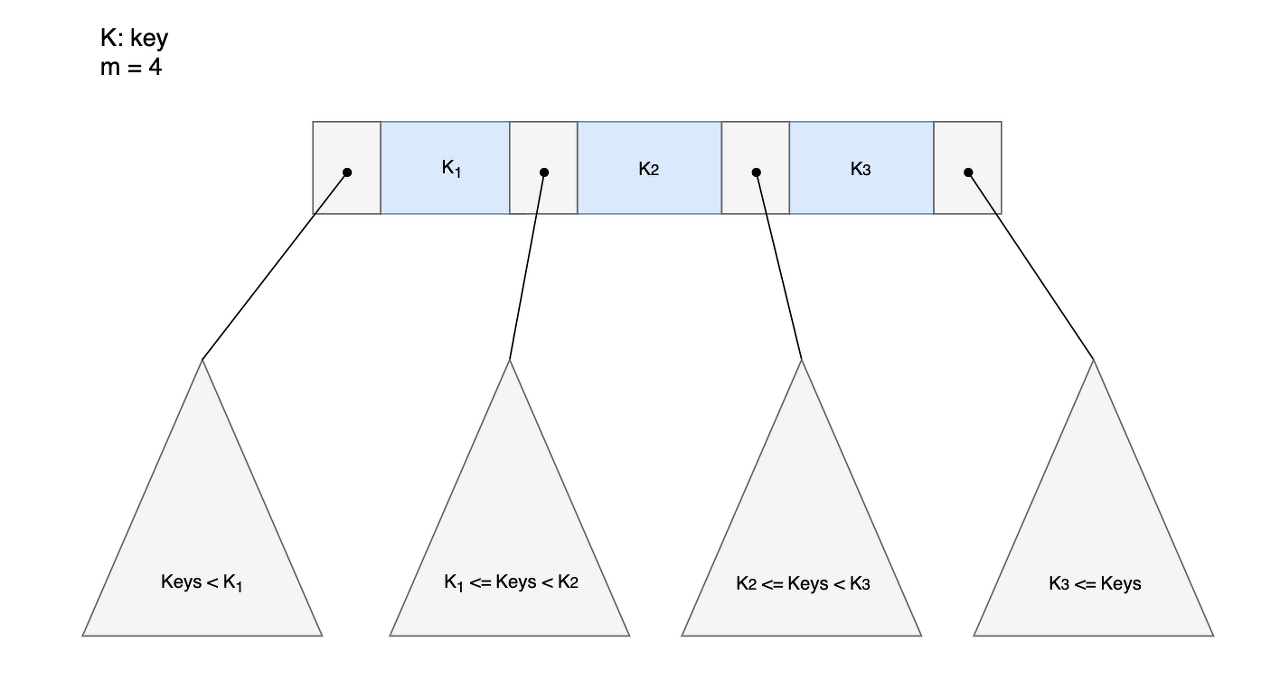
• 다원 탐색 트리(m-way search tree)
  최대 m개의 서브 트리를 갖는 탐색 트리
  이진 탐색 트리의 확장된 형태로 높이를 줄이기 위해 사용한다.

• 균형 트리 (Balanced Tree, B-Tree)
  다원 탐색 트리에서 높이 균형을 유지하는 트리

---

트리(Tree) 순회 방식

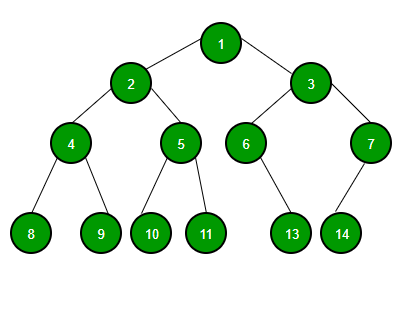
• 전위 순회(preorder traversal)

루트(Root) 에서 시작하여 왼쪽 자식 노드 다음 오른쪽 자식 노드를 탐색하게 하는 방식으로 노드에 값이 존재하지 않을 때까지 순회(재귀)하도록하는 탐색방식이다.

(Root → 왼쪽 자식 → 오른쪽 자식)

1 → 2 → 4 → 8 → 9 → 5 → 10 → 11 → 3 → 6 → 13 → 7 → 14

• 중위 순회(inorder traversal)

현재 노드의 왼쪽 자식노드부터 시작해서 루트(Root), 그리고 마지막으로 오른쪽 자식 노드를 순회하는 방법이다.

(왼쪽 자식 → Root → 오른쪽 자식)

8 → 4 → 9 → 2 → 10 → 5 → 11 → 1 → 6 → 13 → 3 →14 → 7

• 후위 순회(postorder traversal)

왼쪽 하위 트리부터 하위를 모두 방문 후 루트(Root)를 방문하는 방식이다.

(왼쪽 자식 → 오른쪽 자식 → Root)

8 → 9 → 4 → 10 → 11 → 5 → 2 → 13 → 6 → 14 → 7 → 3 → 1

• 레벨 순회 (level-order)

루트(Root)부터 계층 별로 방문하는 방식이다.
level(depth)순으로 위에서 아래로 그리고 왼쪽부터 오른쪽으로 순회하는 방법이다.

1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9 → 10 → 11 → 13 → 14

---

트리(Tree)의 사용

• 계층적 데이터 저장
  트리는 데이터를 계층 구조로 저장하는 데 사용된다.
  예를 들어 파일 및 폴더는 계층적 트리 형태로 저장된다.

• 효율적인 검색 속도
  효율적인 삽입, 삭제 및 검색을 위해 트리 구조를 사용한다.

• 힙(Heap)
  트리로 구성된 자료 구조

• 데이터 베이스 인덱싱
  데이터베이스 인덱싱을 구현하는데 트리를 사용한다.
  ex) B-Tree, B+Tree, AVL-Tree..

• Trie
  사전을 저장하는 데 사용되는 특별한 종류의 트리

---

참고자료

https://www.geeksforgeeks.org/binary-tree-data-structure/

링크