🔥핵심 아이디어 : 앞의 숫자가 클 수록 큰 수이다
Sol 1 :
def solution(number, k):
answer = ''
total_length = len(number) - k
number_list = list(number)
idx = 0
cnt = 0
while k > 0:
temp = number_list[idx: idx+k+1]
# max 값 찾기
max_num = max(temp)
max_idx = temp.index(max_num)
print(max_idx, max_num, k)
# max 값 기준 앞에 지우기
answer += max_num
k -= max_idx
idx += max_idx + 1
print(idx, max_idx, max_num, k)
if k == 0 and len(answer) != total_length:
answer += number[-(total_length - len(answer)):]
# if cnt == 2 :
# break
# cnt += 1
return answer- 입력 숫자 범위가 2 ~ 1,000,000이기 때문에 완전 탐색으로 접근하면 무조건 시간 초과가 날 것 같았다
temp[idx : idx+k+1]의 배열을 만들어서 k+1개 부분 수열의 최댓값을 고르고, 그 앞에 숫자들을 다 제거하는 방식으로 접근했다.- 이 과정을 반복하고, k개를 다 제거했는데도 숫자가 모자르다면 모자른 개수만큼 number에서 거꾸로 읽어와 붙여줬다.
- 그런데 이미 while문에 max()함수를 써버려서 O(n^2)가 되어서 시간 초과가 난 것 같다..
- 또한 number의 길이가 길고 k가 클 때, 이 반복적인 슬라이싱과 검색 연산이 시간 복잡도를 높인다
Sol 2 : Stack 이용
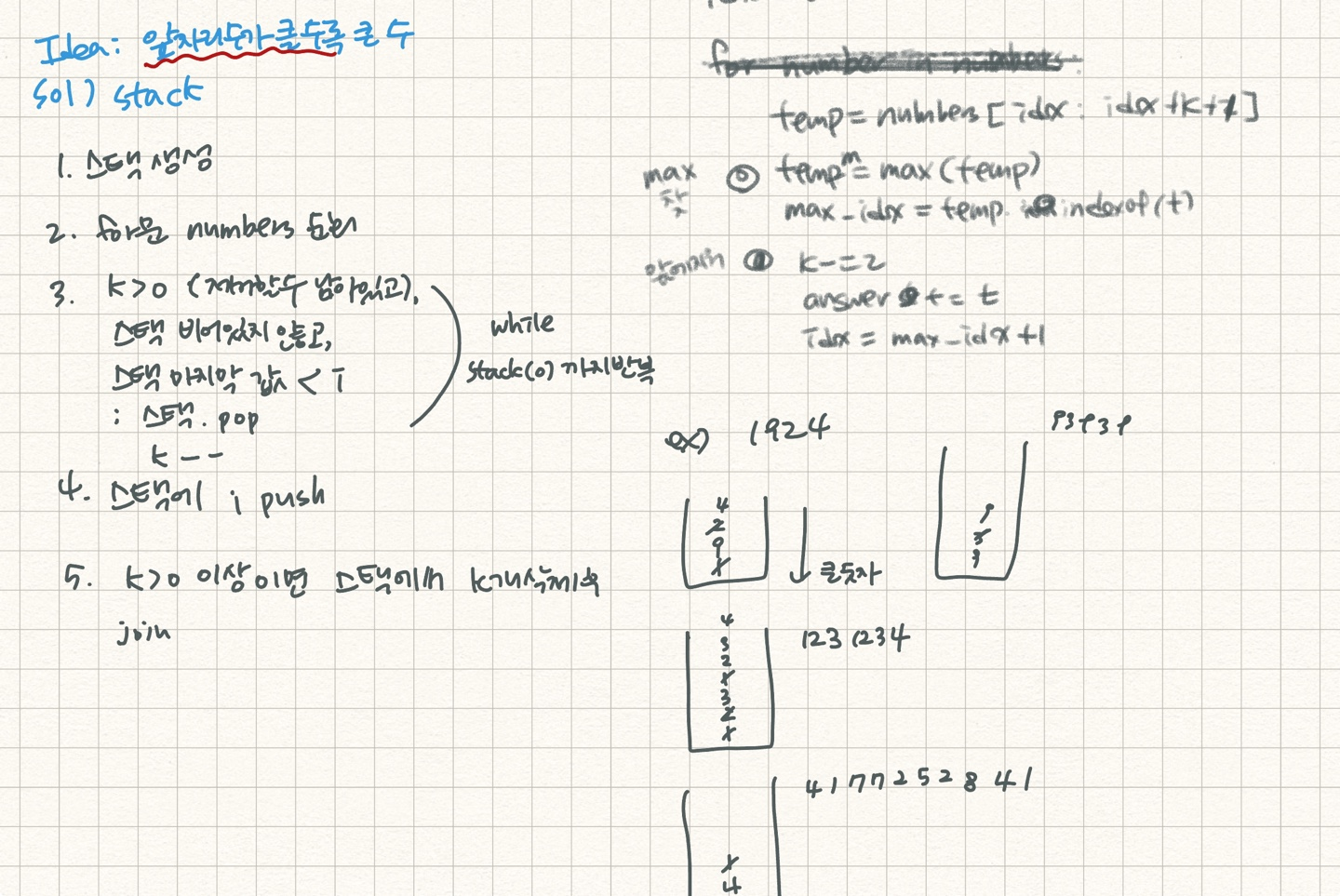
def solution(number, k):
# stack :: 수가 차례대로 담김(큰수부터)
stack = []
for num in number:
# 제거할 수 k가 남아있고
# 스택에 값이 있고
# 스택의 마지막 값이 num보다 작다면
# 제거 후 제거할 수 k 없데이트
while (k > 0) and (stack) and (stack[-1] < num):
stack.pop()
k -= 1
# 값 추가
stack.append(num)
# k가 남아있는 경우
if k > 0:
stack = stack[:-k]
return "".join(stack)
- Stack 구조 이용 :
O(N)
- 숫자를 왼쪽부터 하나씩 살펴보면서, 현재 숫자가 마지막 스택의 숫자보다 크다면, 스택의 마지막 숫자를 제거(pop) (k가 남아있어야 함)-
k를 모두 사용했거나, 스택이 빌 때까지 반복
-
그리고 현재 숫자를 스택에 추가(push)
- 결과를 저장할 빈 스택(파이썬 리스트로 사용 가능)을 만듭니다.
- 입력 문자열 number의 각 숫자를 순서대로 하나씩 살펴봅니다.
- 현재 숫자를 스택에 추가하기 전에 다음을 반복합니다.
스택이 비어있지 않고, k > 0이며, 스택의 마지막 숫자가 현재 숫자보다 작다면, 스택의 마지막 숫자를 제거(pop)하고 k 값을 1 감소시킵니다.
이 과정은 현재 숫자보다 작은 앞선 숫자들을 제거하여 현재 숫자가 더 앞쪽 자리에 오게 함으로써 더 큰 수를 만들기 위함입니다. - 위 과정을 마친 후, 현재 숫자를 스택에 추가(push)합니다.
- number의 모든 숫자를 다 살펴본 후에도 k > 0이라면 (이는 뒤쪽으로 갈수록 숫자가 커지거나 같아서 앞쪽에서 제거할 기회가 없었다는 뜻), 스택의 뒤에서 남은 k개만큼 숫자를 제거합니다.
- 스택에 남아있는 숫자들을 순서대로 이어 붙여 최종 결과 문자열을 만듭니다.
-
Stack: 맨 앞 자릿수를 크게 만들기 위한 임시 저장소
어떻게 Stack 자료구조를 생각했을까....
문제를 보자마자 "가장 앞자리에 가장 큰 수가 와야한다"라는 아이디어는 생각했는데, 그 뒤에 구현하는 부분에서 생각한 풀이가 달랐다. stack은 생각도 못해봤다. 그래서 stack 자료구조를 선택하여 풀이를 구상하는 과정을 찾아봤다.
우선 숫자는 왼쪽부터 순서대로 살펴본다. 각 숫자를 보고 최종 결과에 포함 시킬까 말까를 결정해야 한다. 현재 숫자를 결정할 때, 이미 최종 결과의 앞부분으로 결정된 숫자들과 비교도 해야한다.
지금 숫자가 이전 숫자보다 크다면?
예를 들어 31까지 결정했는데, 다음 숫자로 9가 등장한다면? 9는 1보다 크니까 1을 제거해야하고, 3보다 크니까 3도 제거해야한다.
이렇게 이전에 결정된 숫자보다 커서 이전 숫자를 제거하고 싶다면, 이전에 결정한 숫자를 제거해야 한다. 가장 최근에 저장한 것 부터 제거-> 제거 & 되돌림의 반복
LIFO 패턴 : "가장 최근에 넣은 것을 가장 먼저 꺼낸다" 는 특징을 가지고 있다. 따라서 스택 자료구조와 특성을 통해 구현할 수 있었다.
- 스택에 최종 결과를 구성할 숫자들을 차례로 쌓는다
- 새로운 숫자가 들어올 때마다 스택의 맨 위 숫자와 비교한다
- 만약 새 숫자가 스택 맨 위 숫자보다 크고, 아직 k를 사용할 여유가 있다면, 스택 맨 위 숫자를 제거하여 k를 소진한다.
- 그냥 pop으로 제거해도 되는 이유는 그 숫자들보다 큰 숫자가 나와서 앞의 숫자들은 필요가 없기 때문에 stack에서 제거해버리는 것이다 -> " 앞 자리가 클 수록 큰 수가 된다 "는 핵심 아이디어 때문에 - 그 후, 새 숫자를 스택에 추가한다.
이렇게 하면 스택에는 항상 현재까지 처리된 숫자들로 만들 수 있는 가장 큰 수의 앞 부분이 유지가 된다!
순차적으로 입력 값을 처리하면서, 현재 값을 기준으로 이전에 처리한 값 중 가장 마지막 값을 판단하여 제거하거나 유지하는 작업이 반복될 때 : stack
