[알고리즘] 정렬 (선택, 버블, 삽입, 병합, 퀵, 힙)

히끼·2024년 3월 7일

TIL 내일배움캠프 알고리즘

TIL

목록 보기

18/43

정렬

정렬(sort) : 주어진 데이터를 기준에 따라서 나열하는 것 (오름차순, 내림차순 등)
내부 정렬 : 모든 데이터를 주기억장치에 적재한 후 정렬하는 방식
- 정렬 방식에는 비교 기반과 분포 기반이 있음
- 비교 기반 : 두 개의 데이터를 직접 비교해서 정렬하는 방식
  - $O(n^2)$ → 기본적인 형태의 정렬 알고리즘 → 선택 정렬, 버블 정렬, 삽입 정렬
  - $O(n\log n)$ → 기본 형태를 개선시킨 형태의 알고리즘 → 퀵 정렬, 합병 정렬

선택 정렬 (selection sort)

주어진 데이터 중에서 가장 작은 값부터 차례대로 ‘선택’해서 나열하는 방식

과정

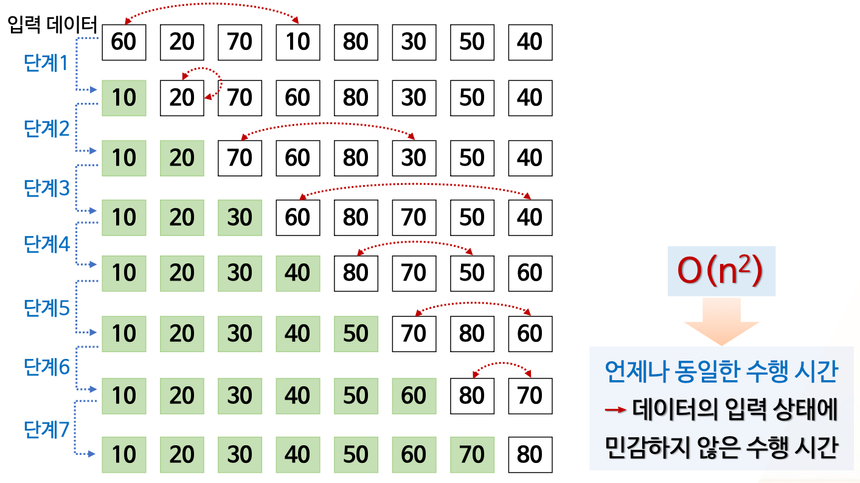
(1단계) 정렬되지 않은 데이터 중 최소값 10 선택 → 미정렬 데이터 중 첫번째 원소 60과 자리 바꾸기

- 최소값 찾기까지 (n-1)번 비교함

(2단계) 정렬되지 않은 데이터 중 최소값 20 선택 → 미정렬 데이터 중 첫번째 원소 20이므로 자리 유지

- 최소값 찾기까지 (n-2)번 비교함

(n-1단계) 반복

- 총 1+2+3+…+(n-1)번 비교함 → $\frac {n(n-1)} 2$
    
    → $O(n^2)$

언제나 동일한 수행 시간 $O(n^2)$ (데이터가 어떻게 주어지든, 같은 횟수만큼 비교함) → 데이터의 입력 상태에 민감하지 않은 수행 시간

버블 정렬 (bubble sort)

왼쪽에서부터 모든 인접한 두 데이터를 차례대로 비교하여 왼쪽의 값이 더 큰 경우에는 오른쪽 값과 자리를 바꾸는 과정을 통해 정렬

과정
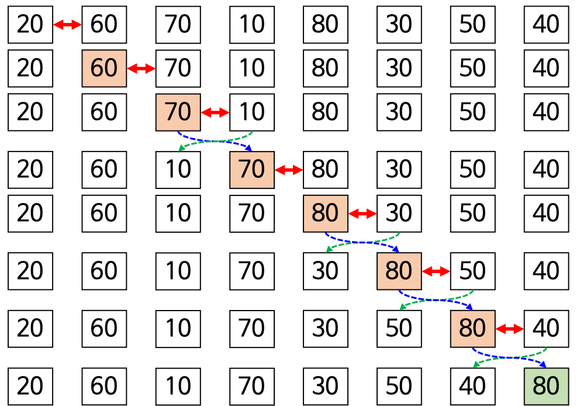
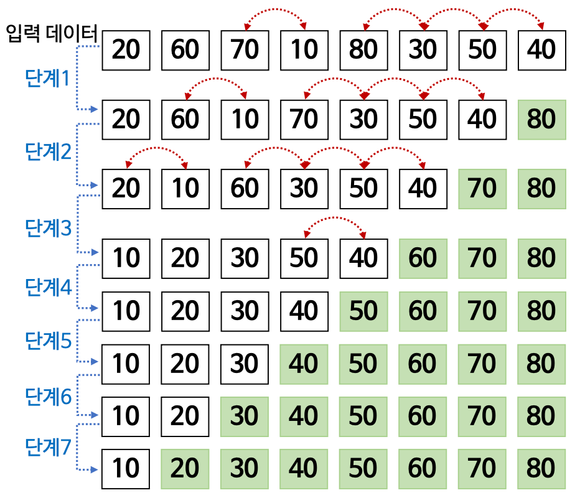
1. 왼쪽부터 오른쪽 끝까지 버블 정렬을 진행한다. 한 단계가 끝나면 가장 큰 값이 가장 오른쪽에 온다.
2. 1에서 가장 마지막에 온 값(80)을 제외한 나머지를 기준으로 다시 왼쪽부터 오른쪽으로 진행한다.
3. 위 과정을 반복하면, 4단계를 마친 후 부터는 자리가 변경되지 않는다. 5단계를 진행 후에도 자리가 바뀌지 않는다면, 6, 7단계는 생략이 가능하다.
데이터의 입력 상태에 따라 성능이 달라짐
- 원하는 순서로 이미 정렬되어 있는 경우 → 최선의 경우 $O(n)$
- 역순으로 정렬되어 있는 경우 → 최악의 경우 $O(n^2)$
  - 알고리즘 수행 시간은 보통 최악으로 나타내므로, 버블 정렬은 $O(n^2)$
선택 정렬에 비해 데이터 교환이 더 많이 발생
- 같은 $O(n^2)$ 이라도 선택 정렬보다 비효율적

삽입 정렬 (insertion sort)

주어진 데이터를 하나씩 뽑은 후,

나열된 데이터들이 항상 정렬된 형태를 가지도록 뽑은 데이터를 바른 위치에 ‘삽입’해서 나열하는 방식

입력 배열을 정렬 부분과 미정렬 부분으로 구분
- 미정렬 부분의 가장 왼쪽에 있는 데이터(“첫번째 데이터”)를 꺼낸 후, 정렬된 부분에서 제자리를 찾아 삽입하는 과정을 반복
과정
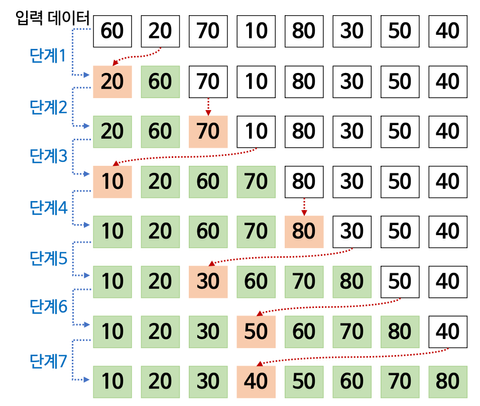
- 첫 번째 데이터는 이미 정렬되었다 가정하고 처리를 시작
- 미정렬 데이터에서 첫번째 데이터 뽑고, 정렬 부분에서 제자리 찾아 삽입하는 과정을 반복
성능은 버블 정렬과 같음
- 데이터의 입력 상태에 따라 성능이 달라짐 데이터가 이미 정렬된 경우와 역순인 경우에 따라 성능이 달라짐
- 최악의 경우의 성능은 $O(n^2)$

병합(합병) 정렬 (merge sort)

동일한 크기의 두 개의 부분배열로 분할하고, 각 부분배열을 순환적으로 정렬한 후,

정렬된 두 부분배열을 병합하여 하나의 정렬된 배열을 만드는 방식

과정
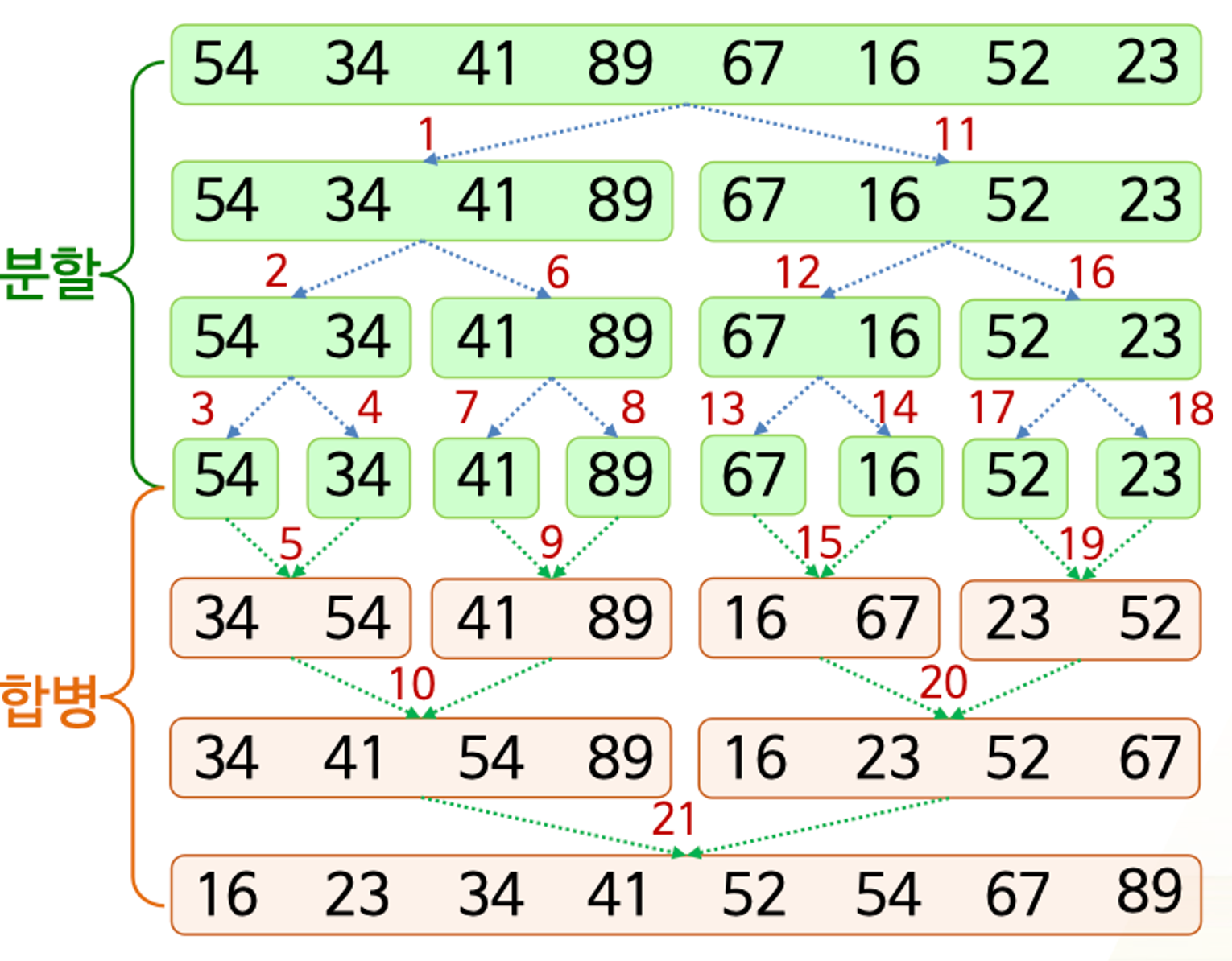
- 쪼갤 수 없을 때까지 (1개일 때까지) 분할
- 1개짜리 합쳐서 정렬된 2개짜리 만들기
- 2개짜리 합쳐서 정렬된 4개짜리 만들기
- (반복)
- 최종적으로 정렬된 결과 얻기

병합 과정

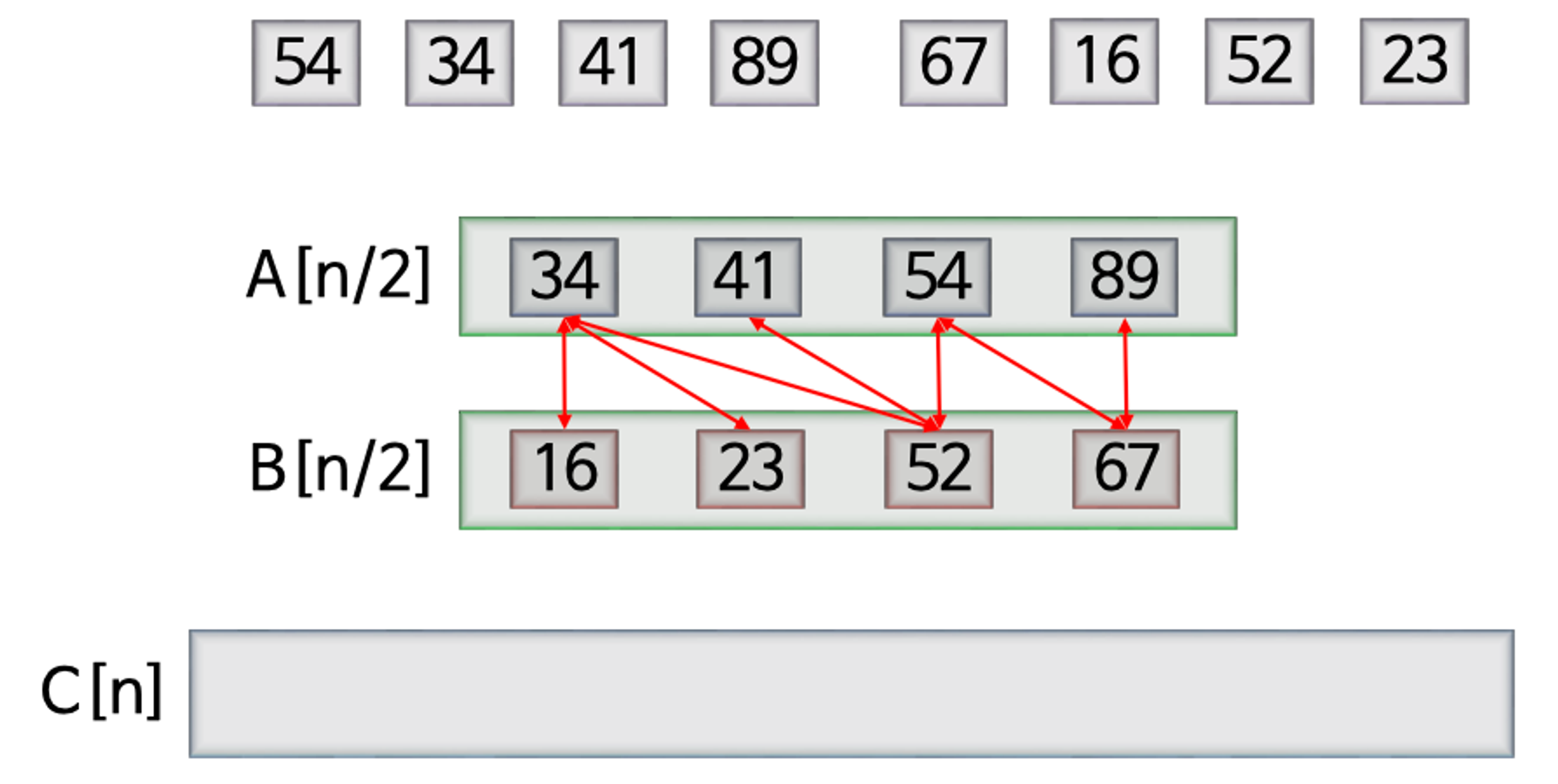
  1. 왼쪽 절반, 오른쪽 절반의 앞부터 비교(34 vs 16)해서 작은 값 16 넣기
  2. 34 vs 23 → 23
  3. 34 vs 52 → 34
  4. (반복)
  5. 89 vs 67 → 67
  6. 남는 89를 넣기 ⇒ 정렬된 하나의 부분 배열

분할정복 방법을 적용한 알고리즘
- 분할 : 정렬할 n개의 데이터를 n/2개의 데이터를 갖는 두 부분배열로 분할
- 정복 : 두 부분배열에 대해 병합 정렬을 각각 순환적으로 적용하여 정렬한다
- 결합 : 정렬된 두 부분배열을 병합하여 하나의 정렬된 배열을 만듦
최선, 최악, 평균 수행 시간 → $O(n\log n)$

퀵 정렬 (quick sort)

특정 데이터를 기준으로 입력 배열을 두 부분배열로 분할하고, 각 부분배열에 대해서 독립적으로 퀵 정렬을 순환적으로 적용하는 방식
피벗 (pivot, 분할원소) : 두 개의 부분배열로 분할할 때 기준이 되는 데이터
- 보통 주어진 배열의 첫 번째 원소로 지정
퀵 정렬 : 피벗이 제자리를 잡도록 하여 정렬하는 방식
- 왼쪽 부분배열의 모든 값 < 피벗 < 오른쪽 부분배열의 모든 값
- 위의 조건이 되도록 피벗의 자리를 잡고, 그 피벗을 기준으로 왼쪽과 오른쪽으로 분할함 → 각 부분배열에 대해 퀵 정렬을 다시 적용
과정
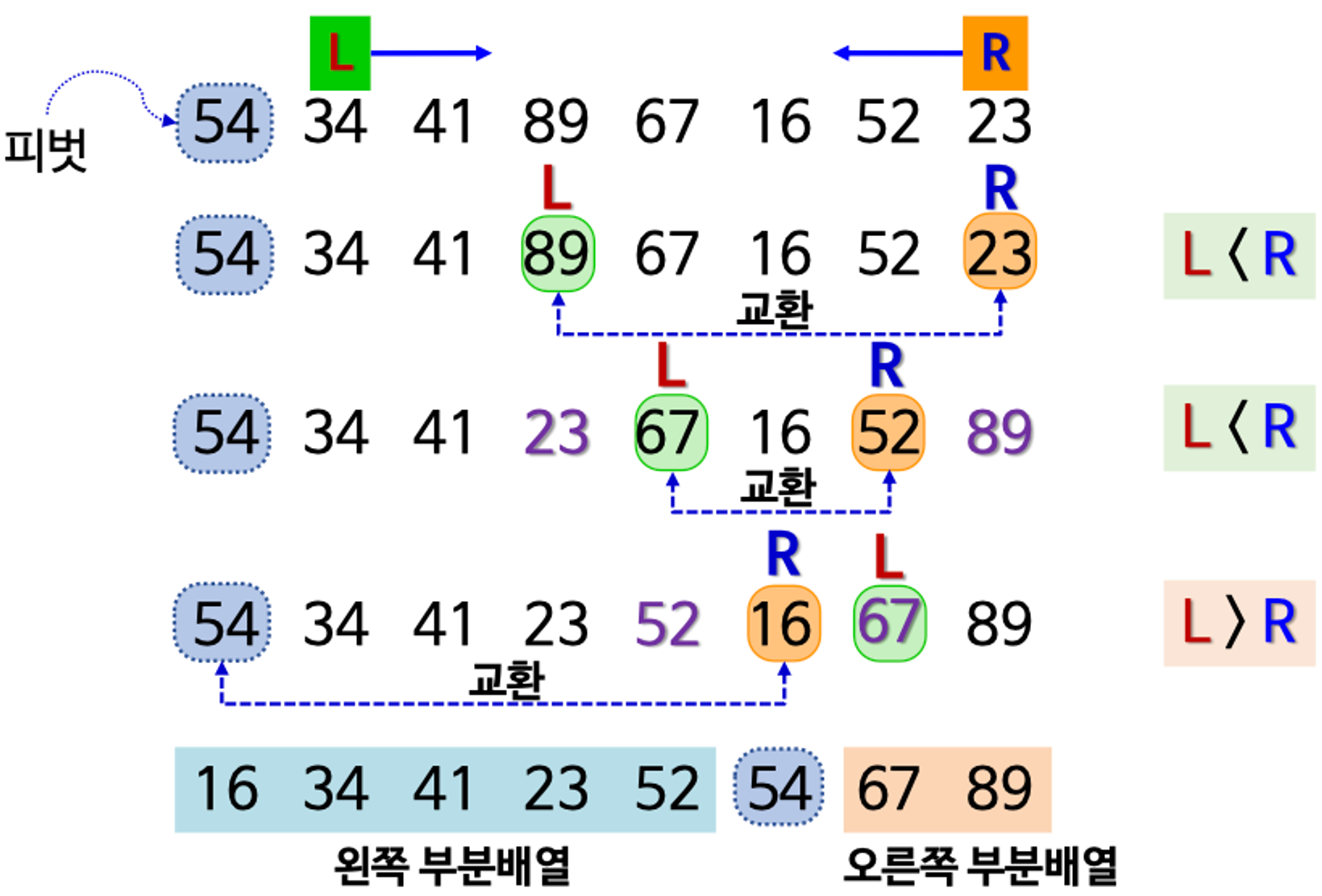
- L 포인터 : 피벗 다음 데이터를 가리킴
  - 왼쪽 → 오른쪽 진행하면서 피벗보다 큰 값을 찾음
- R 포인터 : 맨 끝 데이터를 가리킴
  - 오른쪽 → 왼쪽 진행하면서 피벗보다 작은 값을 찾음
1. L 포인터 기준 89를 찾고, R 포인터 기준 23을 찾음 (L<R)
2. 각 포인터가 가리키는 값의 위치를 바꿈 (L<R)
3. 다시 찾고, 위치 바꾸기를 반복 (L<R)
4. L이 R보다 더 오른쪽에 오게 되면, 찾기 종료 (L>R)
5. 마지막 R 포인터가 가리키는 값과 피벗의 자리 바꿔서 피벗이 제자리를 잡고, 분할 종료
  
  → 해당 과정을 계속 반복 (피벗을 기준을 분할만 계속 진행)
분할정복 방법을 적용한 알고리즘
- 분할 : 정렬할 n개 데이터를 피벗을 중심으로 두 개의 부분배열로 분할
- 정복 : 두 부분배열에 대해 퀵 정렬을 각각 순환적으로 적용하여 두 부분배열을 정렬
평균적으로 가장 좋은 성능의 비교 기반 알고리즘 → $O(n\log n)$
- 피벗 선택의 임의성(랜덤 선택)만 보장되면, 최악이 아닌 평균 수행 시간( $O(n\log{n})$ )을 보일 가능성이 높음 → 평균 수행 시간이 가장 빠른 알고리즘

힙 정렬 (heap sort)

힙 (Heap)

부모-자식 노드 사이에서 부분적으로 정렬된 완전 이진 트리
부모 노드는 자식 노드보다 우선 순위가 높음

💡 트리 (tree)
노드 혹은 정점으로 구성된 논리적인 계층이 있는 구조

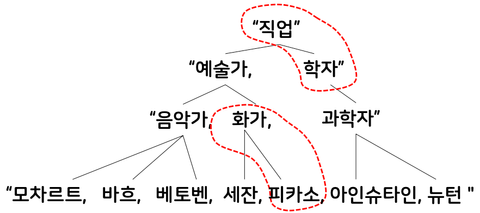
노드 : 트리를 구성하는 항목 단위 (예: 직업, 예술가, 화가, 뉴턴)
부모 노드 - 자식 노드 : 상하 계층 구조를 갖고 직접적으로 연결된 노드
- 부모 노드 : 상위 계층의 노드
- 자식 노드 : 하위 계층의 노드
- 예 : 화가-피카소, 직업-학자
루트 노드 : 진입 차수가 0인 노드 (예: 직업)
잎 노드 : 진출 차수가 0인 노드 (예: 모차르트, 뉴턴)
레벨 : 루트 노드부터 해당 노드까지 이어진 선의 길이 (예: 레벨 2 - 음악가, 화가, 과학자)

💡 이진 트리 (binary tree)
모든 노드가 2개 이하의 자식 노드를 갖는 트리

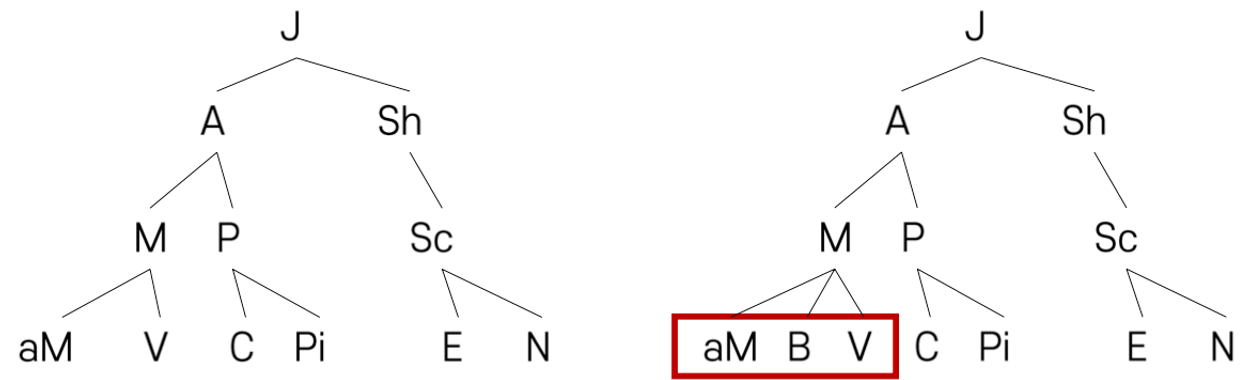
왼: 이진 트리 / 오: 이진 트리 아님

💡 완전 이진 트리 (complete binary tree)
마지막 레벨을 제외한 모든 레벨이 완전히 채워지고, 마지막 레벨은 왼쪽부터 오른쪽으로 차례로 채워진 이진 트리

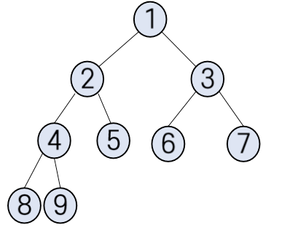
최소 힙 : 루트가 가장 작은 값을 갖고 부모는 자식보다 작은 값을 가지는 힙
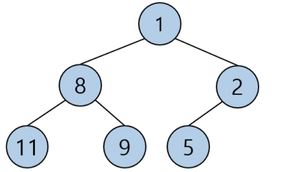
최대 힙 : 루트가 가장 큰 값을 갖고 부모는 자식보다 큰 값을 가지는 힙

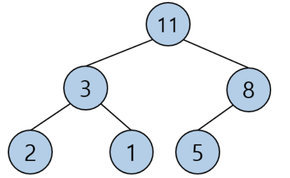
힙 정렬 (Heap Sort)

힙 구조를 사용하여 데이터를 정렬하는 방식
정렬 방법

예) 무작위로 주어진 수(6 9 10 4 5 1 12 3)를 오름차순으로 정렬한다.
1. 데이터 삽입 순서대로 이진 탐색 트리를 만든다.
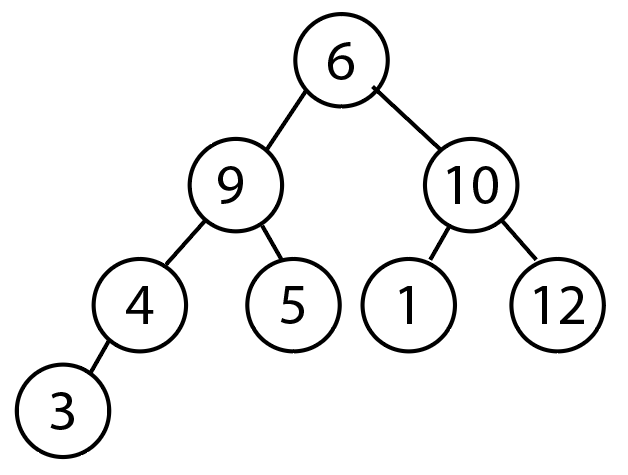
2. 부모 노드보다 값이 큰 자식 노드는 부모 노드와 교환하여, 최대 힙을 구현한다.
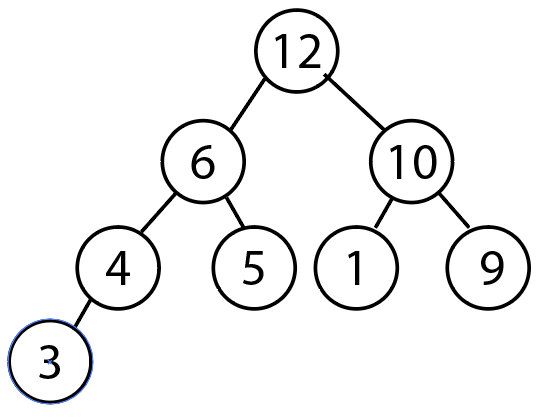
3. 루트 노드(12)를 마지막 노드(3)와 교환하고 다시 힙 구조로 재배열 한다. 교환된 루트 노드(12)는 정렬을 확정한다.
4. 정렬이 확정된 노드를 제외한 나머지 노드들을 기준으로 3의 과정을 반복한다.
5. 모든 과정을 반복하면 배열이 오름차순으로 정렬된다.
시간 복잡도
- 힙에서 가장 큰(또는 작은) 노드를 마지막 노드와 교환하고, 힙 크기를 줄여서 힙 구조를 유지함 → 힙의 크기가 n일 때, 위의 한 번의 과정에 $\log n$ 의 시간이 걸림 → 힙의 모든 요소에 대해 과정을 수행하므로, $O(n\log n)$
장점
- 제자리에서 정렬을 하므로, 추가적인 메모리가 필요하지 않음
- 최선, 평균, 최악의 경우 모두 힙 구성 과정(heapify)이 필요하여 $O(n\log n)$ 을 보장한다. (일정한 성능을 보장함)
- 최악의 경우에도 일정한 시간 복잡도를 보장하므로, 데이터가 많을 때 유용하게 사용될 수 있음
단점
- 숫자가 같은 경우에도 교환이 일어날 수 있어, 안정적이지 않음
- 입력 데이터의 순서를 보존하지 않음
- 데이터 개수가 적을 때는 성능이 좋지 않을 수 있음