1. 알고리즘 분석
- 정확성 분석
- 유효한 입력에 대해 유한 시간 내에 정확한 결과의 생성 여부
- 수학적 기법을 사용한 이론적인 증명 과정
- 유효한 입력에 대해 유한 시간 내에 정확한 결과의 생성 여부
- 효율성 분석
- 알고리즘 수행에 필요한 컴퓨터 자원의 양을 측정/평가
- 공간 복잡도 (space complexity)
- 메모리의 양 = 정적 공간 + 동적 공간
- 시간 복잡도 (time complexity)
- 수행시간 = 알고리즘의 실행에서부터 완료까지 걸리는 시간
공간 복잡도는 메모리 성능에 따라 달라질 수 있고, 기술의 발전으로 대부분의 메모리 성능이 좋아져,
최적화를 하기에 더 용이한 시간 복잡도를 알고리즘에서 더 중요하게 다루는 편이다.
2. 시간 복잡도
- 알고리즘 수행시간 = ∑{각 문장(연산)이 수행되는 횟수} ⭐
- 수행시간에 영향을 미치는 요인
- 입력 크기 → ”입력되는 데이터의 크기”, “문제가 해결하려는 대상이 되는 개체의 개수” → 예: 리스트 원소의 개수, 행렬의 크기, 그래프의 정점의 수 등
- 입력 데이터의 상태
- 입력 크기 → ”입력되는 데이터의 크기”, “문제가 해결하려는 대상이 되는 개체의 개수” → 예: 리스트 원소의 개수, 행렬의 크기, 그래프의 정점의 수 등
- 수행시간에 영향을 미치는 요인
📌 알고리즘 수행 시간은 입력 크기 𝑛 의 함수와 최악의 수행시간으로 표현
- 입력 크기 𝑛 이 커질수록 수행시간도 증가
- 단순히 단위 연산이 수행되는 개수의 합으로 표현하는 것은 부적절 → 입력 크기 𝑛 의 함수 𝑓(𝑛)으로 표현
- 단순히 단위 연산이 수행되는 개수의 합으로 표현하는 것은 부적절 → 입력 크기 𝑛 의 함수 𝑓(𝑛)으로 표현
- 입력 데이터의 상태에 종속적
-
평균 수행시간 →
- 입력 데이터의 모든 경우의 수를 고려하기 어려워 현실적으로 사용하기 어려움
-
최선 수행시간 →
-
최악 수행시간 →
- 일반적으로 알고리즘의 시간 복잡도를 표현할 때 사용됨: 크기 𝑛 인 입력들의 집합
: 입력 𝐼 가 발생할 확률
: 입력 𝐼 일 때 알고리즘의 수행시간
-
3. 점근성능
점근성능 : 입력 크기 𝑛 이 무한히 커짐에 따라 결정되는 성능
점근성능의 결정 방법
- 입력 크기가 충분히 커짐에 따라 함숫값에 가장 큰 영향을 미치는 차수를 찾음
- 수행시간의 다항식 함수에서 최고차항만을 계수 없이 취해서 표현
- 수행시간의 정확한 값이 아닌 어림값 → 수행시간의 증가 추세를 파악하는 것이 쉬움 → 알고리즘 간의 우열을 따질 때 유용
점근성능의 표기법
(1)’Big-oh’ 점근적 상한 (= 최악 수행시간)
함수 f와 g를 각각 양의 정수를 갖는 함수라 하자.
어떤 양의 상수 와 이 존재하여
모든 에 대하여 이면 이다.
(2) ’Big-omega’ 점근적 하한 (= 최선 수행시간)
함수 f와 g를 각각 양의 정수를 갖는 함수라 하자.
어떤 양의 상수 와 이 존재하여
모든 에 대하여 이면 이다.
(3) ’Big-theta’ 점근적 상하한
함수 f와 g를 각각 양의 정수를 갖는 함수라 하자.
어떤 양의 상수 , 와 이 존재하여
모든 에 대하여 이면 이다.
주요 O-표기 간 연산 시간의 크기 관계
(왼쪽) 효율적 ← → 비효율적 (오른쪽)
상수 시간 O(1) < 로그 시간 O(log n) < 선형 시간 O(n) < 로그 선형 시간 O(n log n) < 제곱 시간 O(n^2) < 세제곱 시간 O(n^3) < 지수 시간 O(2^n)
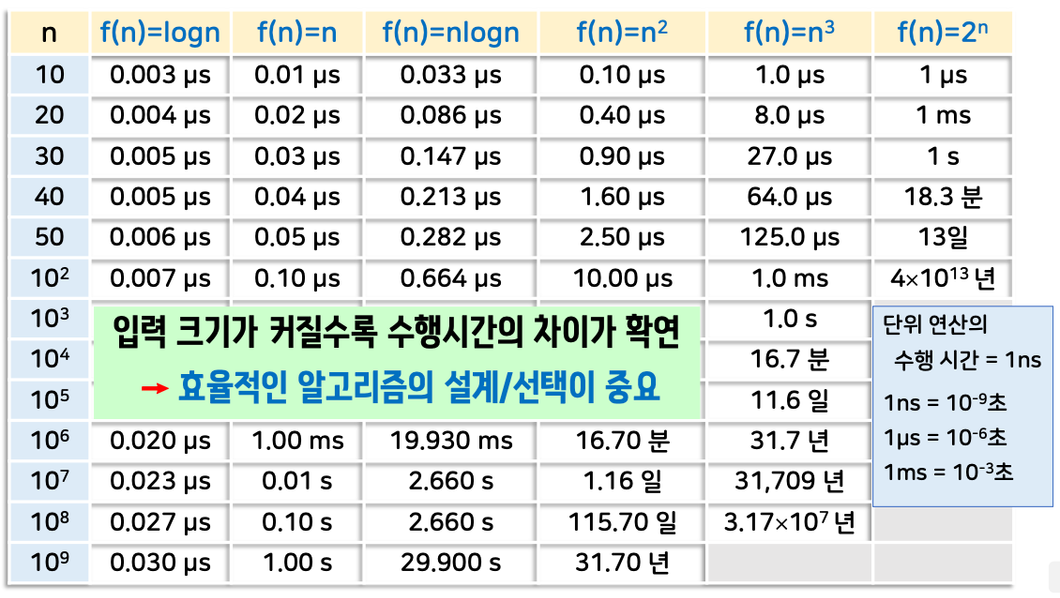
빅오 함수에 따른 연산 시간의 증가 추세

알고리즘의 시간 복잡도 구하기
- 알고리즘의 시간 복잡도를 구하려면
- 기본 연산의 수행 횟수의 합 f(n)을 구한 후,
- f(n)=O(g(n))을 만족하는 최소 차수의 함수 g(n)을 찾음
- 실용적인 접근 방법
- 알고리즘의 모든 문장이 아닌 루프의 반복 횟수만을 조사하여 최고 차수를 시간 복잡도로 취함 → O(최고차수)
- 반복문에서 반복되는 부분이 입력 크기 n 과 어떤 관계를 갖는지에 따라 최고차수를 취함
4. 순환 알고리즘 (recursion, 재귀 알고리즘)
알고리즘의 수행 과정에서 자기 자신의 알고리즘을 다시 수행하는 형태
- 점화식 : 어떤 하나의 값이 자기 자신을 포함하는 수식으로 표현되는 식
- 성능을 알기 위해서는 점화식을 풀어야 함 → 점화식을 풀어서 점화식의 “폐쇄형”이 성능이 됨

입력의 크기가 작을 때는 어떤 성능의 알고리즘을 써도 큰 차이가 나지 않음
하지만, 입력의 크기가 커지면 알고리즘의 성능이 크게 차이가 남 → 효율적인 알고리즘 설계/개발/사용이 중요함