정렬
버블정렬
인접한 두 원소를 순서대로 보면서 정렬해 나가는 알고리즘
오름차순으로 정렬한다고 가정,
1. A[i] 와 A[i+1]을 비교
2. A[i] > A[i+1]이면, A[i], A[i+1]을 교환(swap)
버블 정렬은 순회를 N-1번 반복한다.
*순회란? i=1..N-1까지 순서대로 한번 수행하는 것(N은 배열의 길이)
버블정렬 시간복잡도
길이가 N인 배열을 한번 순회할 때,
- 비교 N-1번 (최대)
- 교환 N-1번 (최대)
i번째, 순회에서 i번째로 큰 값이 뒤에서 i번째 위치로 이동한다.
순회를 N-1번 반복하면 모든 수가 올바른 위치로 이동한다.
(N-1)^이므로 시간복잡도는 O(N^2)
삽입정렬
적절한 위치에 원소를 옮김(삽입함)으로써 정렬해 나가는 알고리즘
i=2...N인 i에 대해서 순서대로 다음과정을 수행한다.
- i번째 작업에서,
- A[i]를 부분배열 [1, i]가 정렬된 상태가 되도록 적절한 위치에 삽입한다.
삽입정렬 시간복잡도
평균적으로, i번째 작업에서 A[i]를 i/2번째 위치로 옮기는 경우
i번째 작업에서 O(N)의 시간이 걸린다고 할 수 있다.
작업을 N번 수행해야 하므로 시간복잡도는 O(N^2)
퀵정렬
재귀적으로 정렬을 수행하는 알고리즘
sort(int A[])
1. 배열 A의 길이가 0 또는 1이면, 이미 정렬된 배열이므로 함수 종료
2. 배열 A에 있는 아무 원소를 pivot으로 잡는다.
- pivot보다 작은 원소를 pivot의 왼쪽으로 옮기고
- pivot보다 큰 원소를 pivot의 오른쪽으로 옮긴다.
- pivot을 기준으로 왼쪽에 있는 배열에 대해서 sort를 다시 호출한다.(왼쪽 배열을 다시 정렬)
- pivot을 기준으로 오른쪽에 있는 배열에 대해서 sort를 다시 호출한다.(오른쪽 배열을 다시 정렬)
퀵정렬 시간복잡도
- 평균적으로, 매번 고르는 pivot이 왼쪽, 오른쪽 배열을 정확히 절반씩 나누는 경우,
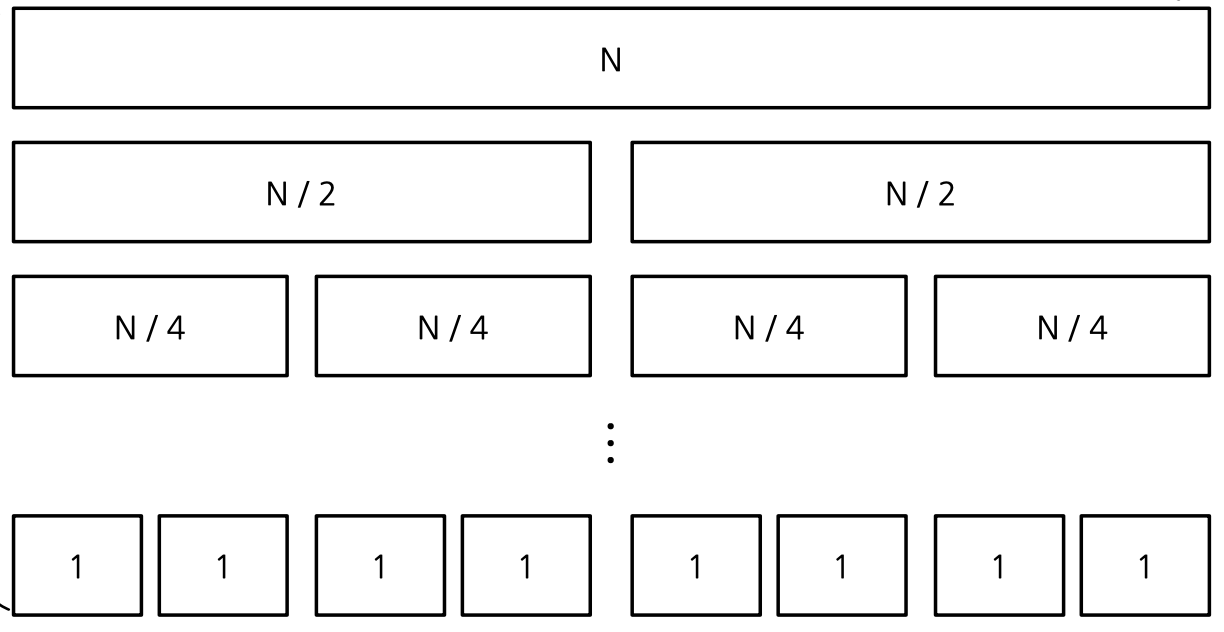
- 호출 깊이가 같은 sort 함수끼리 시간복잡도 함은 O(N)
- 배열을 정확히 절반씩 나누기 때문에 호출 깊이는 O(logN)
시간복잡도는 O(NlogN)
- worst의 경우, pivot이 불균형하게 나누는 경우,
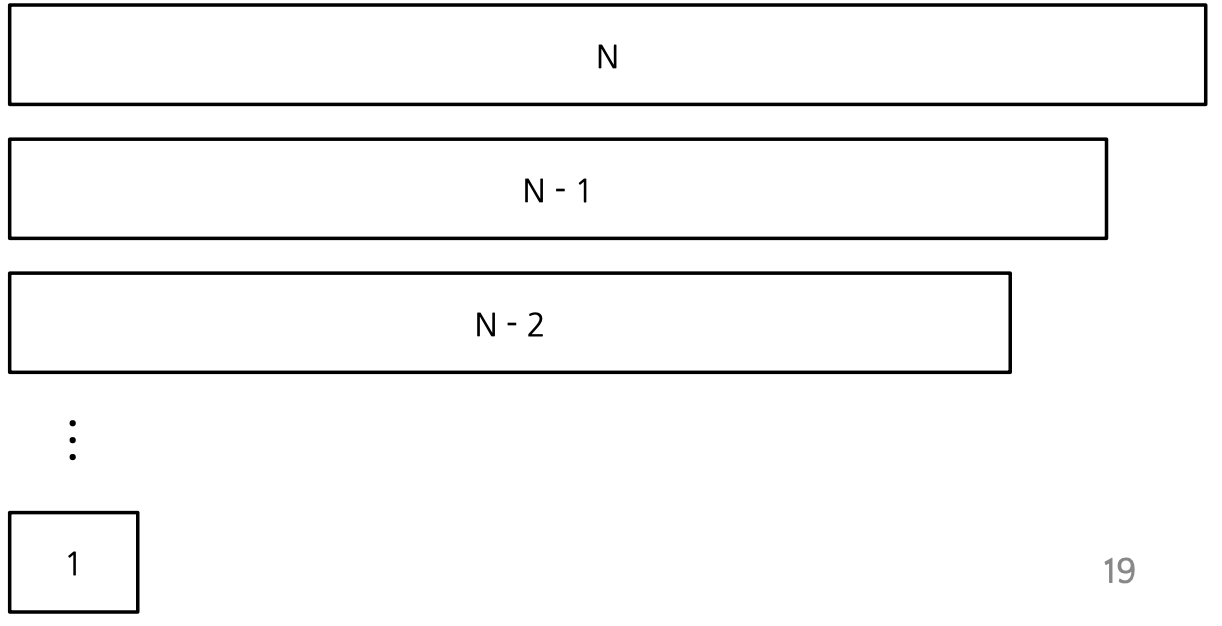
- 호출 깊이가 i인 sort 함수에서 필요한 연산량은 n-i정도이므로 O(N)
- 호출 깊이는 배열의 길이가 1이 될 때까지 반복되므로 O(N)
시간복잡도는 O(N^2)
병합정렬(Merge Sort)
재귀적으로 정렬을 수행하는 알고리즘
sort(int A[])
1. 배열 A의 길이가 0 또는 1이면, 이미 정렬된 배열이므로 함수 종료
2. 배열 A를 다음 두 배열로 나눈다.
- 왼쪽 절반을 L, 나머지 오른쪽 절반은 R이라고 하자.
- Sort(L)을 호출 (왼쪽 배열을 정렬)
- Sort(R)을 호출 (오른쪽 배열을 정렬)
- 정렬된 두 배열 L과 R을 합쳐서 정렬된 배열 A를 반환한다.
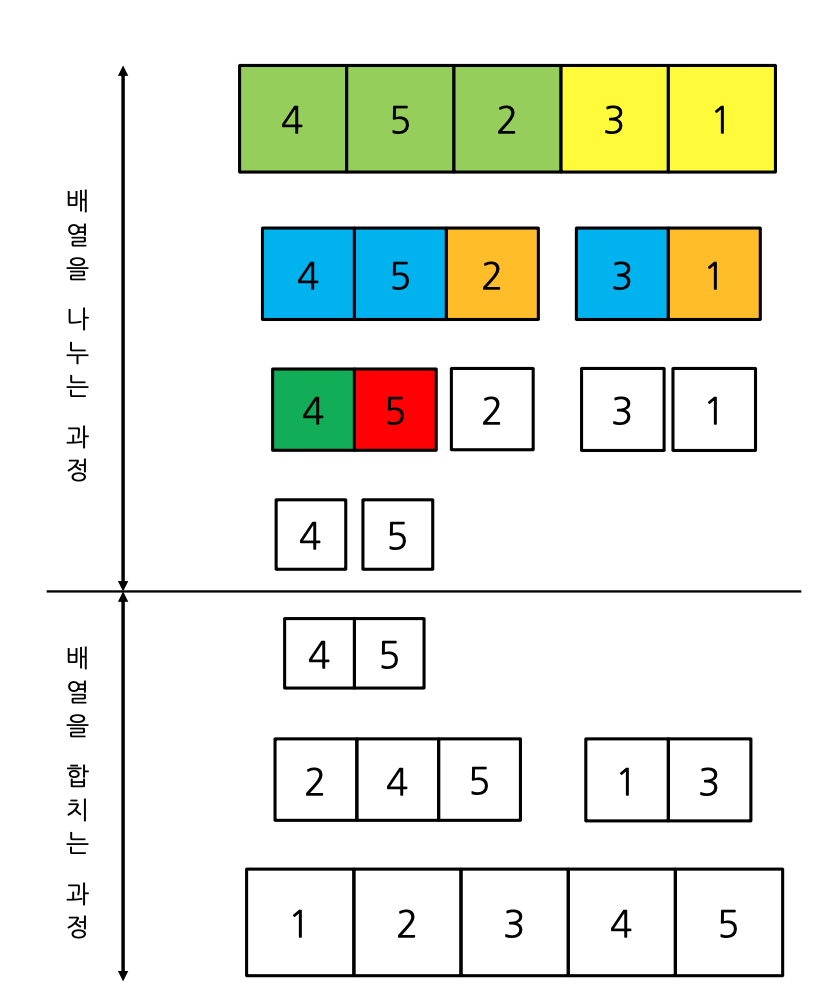
병합정렬 시간복잡도
퀵정렬의 best 경우와 동일하다.
시간복잡도는 O(NlogN)
선형 자료 구조
하나의 데이터 뒤에 하나의 데이터만 올 수 있는 데이터 구조
*비선형 자료 구조란? 하나의 데이터 뒤에 여러 데이터가 올 수 있는 데이터 구조
배열
자료가 물리적으로 연속(= 메모리상에서 연속)되어 저장되는 자료구조
- 임의 위치 접근(= random access) : O(1)
- 원소 삽입/삭제 : O(N)
연결 리스트
자료가 논리적으로 연속(= 메모리 상에서 연속되어 있지 않음)되어 저장되는 자료구조
- 임의 위치 접근(= random access) : O(N)
- 원소 삽입/삭제 : O(1) → 인접한 노드의 주소 정보만 바꿔주면 된다.
노드는 데이터와 자신과 인접한 노드의 주소를 저장한다.
스택 (LIFO)
나중에 들어온 자료가 먼저 나온다.
- push(x) : x를 스택에 넣는다.
- pop() : 스택에서 가장 마지막에 추가된 원소를 뺀다.
큐 (FIFO)
먼저 들어온 자료가 먼저 나간다.
- push(x) : x를 큐에 넣는다.
- pop() : 큐에서 가장 먼저 들어온 원소를 뺀다.
→ 효율적인 구현은 연결리스트로 가능하다.
덱 (LIFO, FIFO)
LIFO, FIFO를 모두 지원하는 자료구조
- push_back(x) : 덱의 가장 뒤에 x를 넣는다.
- push_front(x) : 덱의 가장 앞에 x를 넣는다.
- pop_back() : 덱의 가장 뒤 원소를 제거한다.
- pop_front() : 덱의 가장 앞 원소를 제거한다.
→ 구현은 Doubly Linked List를 사용하고, 맨앞/맨뒤 원소를 저장해두면 된다.
