2021년 8월 25일에 작성된 문서 2번 입니다.
자료 구조 배운 내용을 정리했습니다.

Algorithm with Math - GCD / LCM

• 약수: 어떤 수를 나누어떨어지게 하는 수
• 배수: 어떤 수의 1, 2, 3, ...n 배하여 얻는 수
• 공약수: 둘 이상의 수의 공통인 약수
• 공배수: 둘 이상의 수의 공통인 배수
• 최대 공약수(GCD. Greatest Common Divisor): 둘 이상의 공약수 중에서 최대인 수
• 최소 공배수(LCM. Least Common Multiple): 둘 이상의 공배수 중에서 최소인 수

문제: Mask States

방역용 마스크를 제작/판매하는 Mask States 사는 이례적인 전염성 독감 예방을 위해 기존 가격을 유지하며 약속된 물량의 방역용 마스크를 제공하고 있습니다. 이 회사는 사장을 포함하여 A, B, C 세 명뿐이고, 이들 모두 마스크를 제작합니다. 각각의 제작 속도는 다음과 같습니다. A는 55분마다 9개를, B는 70분마다 15개를, C는 85분마다 25개의 방역용 마스크를 만들 수 있습니다. 이 회사의 사람들은 05:00 시부터 동시에 마스크를 만들기 시작하여 각 55분, 70분, 85분 동안 연속으로 마스크를 제작한 후, 5분씩 휴식을 취합니다. 이들 세 명이 처음으로 동시에 쉬는 시점이 퇴근 시간이라면, 이날 하루에 제작한 마스크는 모두 몇 개인가요? (휴식시간과 퇴근시간이 겹치는 경우, 휴식을 취한 뒤 퇴근합니다.)

이 문제에서 최소공배수를 떠올리면, 쉽고 빠르게 문제를 해결할 수 있다.

• A, B, C의 작업 시간과 쉬는 시간 5분을 더하면 A, B, C는 각각 60분, 75분, 90분마다 마스크를 만든다.
• 세 명이 동시에 휴식을 취하는 시점은 세 명이 쉬고 난 직후가 같을 시점이다.
• 쉬고 난 직후가 처음으로 같을 시점을 구해야 하므로 공배수와 최소 공배수의 개념을 이용해야한다,

결과적으로, LCM(60, 75, 90)은 900

• A는 B, C와 휴식을 취한 직후가 처음으로 같을 시점까지 900/60 = 15 번 작업하고, 15번 X 9개 = 135개의 마스크를 만든다.
• B는 900/75 = 12번의 작업을 반복하고 12턴 X 15개 = 180개.
• C는 900/90 = 10번의 작업을 반복하고 10턴 X 25개 = 250개의 마스크를 만든다.

따라서, A, B, C가 하루에 제작한 마스크의 총 개수는 135개 + 180개 + 250개 = 565개다.

문제: 조명 설치

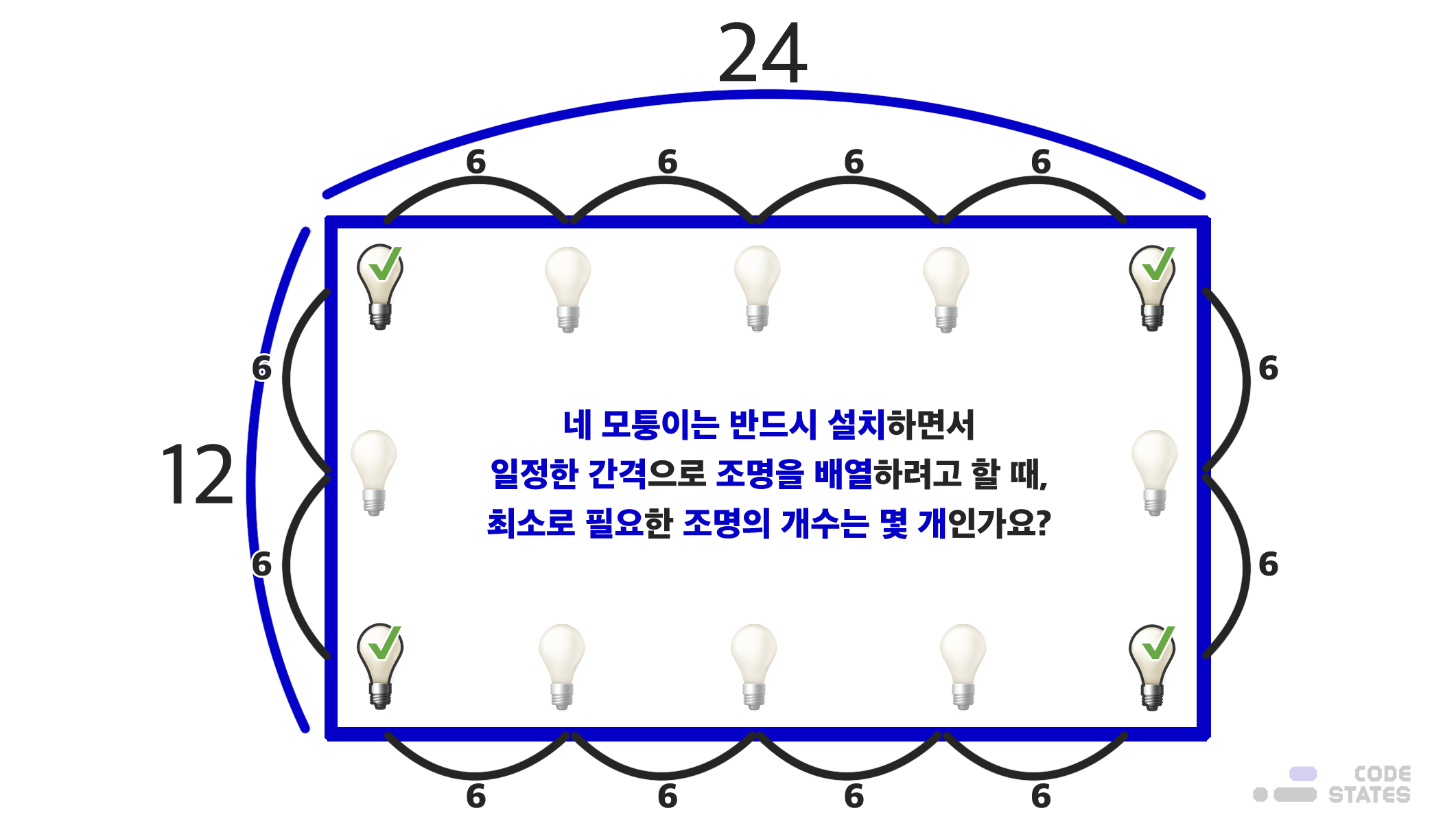
코드스테이츠 라운지에 있는 가로 24cm, 세로 12cm인 직사각형 모양 조형물의 가장자리에 조명을 설치하려고 합니다. 네 모퉁이에는 조명을 반드시 설치해야하고, 나머지 조명은 일정한 간격으로 설치하려고 할 때, 필요한 최소한의 조명 개수는 몇 개일까요? 이때, 꼭지점을 제외한 직사각형의 모든 변에는 최소 하나 이상의 조명이 반드시 설치되어야 합니다. (단, 설치한 조명의 간격은 정수로 이루어진 cm 단위입니다.)

이 문제의 정답은 12개다.

• 모든 조명을 일정한 간격으로 설치해야 하므로, 가로변과 세로변의 공약수를 구해야한다.
  가로와 세로 각각 나누어 떨어지는 수들을 나열한 뒤, 공통된 수만 모으면 공약수를 구할 수 있다.
  공약수를 기준으로 조명을 설치하면, 일정한 간격으로 나누어 조명을 설치할 수 있다.
• 최소로 필요한 조명의 개수를 파악해야 하기 때문에 최대 공약수가 필요하다.

GCD(12, 24)는 12

• 네 모퉁이는 반드시 설치해야 하므로 각 변의 길이를 최대 공약수 12로 나누어 최소로 필요한 조명의 개수를 구할 수 있다.
• (12/12 + 24/12) X 2 = 3 X 2 = 6개

이 문제에서는 꼭지점을 제외한 직사각형의 모든 변에, 최소 하나 이상의 조명이 설치되어야 하므로 12를 제외한 최대 공약수로 문제를 해결해야 합니다.

• (12/6 + 24/6) X 2 = 6 X 2 = 12개

Written with StackEdit.